This text includes characters that require UTF-8 (Unicode) file encoding:
ã ẽ ĩ õ ũ (vowels with overline, shown here as a tilde)
ἐίπερ γὰρ ἀδικεῖμ χρὴ (Greek, mainly in the introduction)
If any of these characters do not display properly—in particular, if the diacritic does not appear directly above the letter—or if the apostrophes and quotation marks in this paragraph appear as garbage, you may have an incompatible browser or unavailable fonts. First, make sure that the browser’s “character set” or “file encoding” is set to Unicode (UTF-8). You may also need to change your browser’s default font.
Unless otherwise noted, spelling, punctuation and capitalization are unchanged. Text in sans-serif type was originally printed in blackletter (“Gothic”, Old English). Typographical errors are marked in the text with mouse-hover popups. Transliteration of single Greek words and short phrases is shown in the same way; the longer Greek passages from the introduction are given at the end of the e-text.
The book does not have page numbers. Instead, it labeled the recto (odd) pages of the first few leaves of each 8-page signature. These will appear in the right margin as A.i., A.ij., A.iij.... Page numbers in brackets, including all verso (v) pages, were added by the transcriber.
Any problems or explanations too long or complicated to fit into a popup are noted either in a separate paragraph or at the end of the e-text.
Full Contents
Principles of Geometry
Conclusions
Axioms
(“Grauntable Requestes”
and “Common Sentences”)
Theorems
Geometries verdicte
All fresshe fine wittes by me are filed,
All grosse dull wittes wishe me exiled:
Thoughe no mannes witte reiect will I,
Yet as they be, I wyll them trye.
[§.i.v]
The argumentes of the foure bookes
The first booke declareth the definitions of the termes and names vsed in Geometry, with certaine of the chiefe grounds whereon the arte is founded. And then teacheth those conclusions, which may serue diuersely in al workes Geometricall.
The second booke doth sette forth the Theoremes, (whiche maye be called approued truthes) seruinge for the due knowledge and sure proofe of all conclusions and workes in Geometrye.
The third booke intreateth of diuers formes, and sondry protractions thereto belonging, with the vse of certain conclusions.
The fourth booke teacheth the right order of measuringe all platte formes, and bodies also, by reson Geometricall.
Contents
(added by transcriber)
Title Page (above)
Arguments of the Four Books (above)
First Book:
To the Gentle Reader
Dedication to King Edward VI
Preface to the First Book
The Principles of Geometry
Conclusions 1–46
Second Book:
Title Page
Preface to the Second Book
Grantable Requests
Common Sentences
Theorems 1–77
TO THE GENTLE READER.
 xcvse me, gentle reder if oughte be amisse, straung paths ar not trodẽ
al truly at the first: the way muste needes be comberous, wher none
hathe gone before. Where no man hathe geuen light, lighte is it to
offend, but when the light is shewed ones, light is it to amende. If my
light may so light some other, to espie and marke my faultes,
I wish it may so lighten thẽ, that they may voide offence. Of
staggeringe and stomblinge, and vnconstaunt turmoilinge: often
offending, and seldome amending, such vices to eschewe, and their fine
wittes to shew that they may winne the praise, and I to hold the candle,
whilest they their glorious works with eloquence sette forth, so
cunningly inuented, so finely indited, that my bokes maie seme worthie
to occupie no roome. For neither is mi wit so finelie filed, nother mi
learning so largly lettred, nother yet mi laiser so quiet and vncõbered,
that I maie perform iustlie so learned a laboure or accordinglie to
accomplishe so
[§.ii.v]
haulte an enforcement, yet maie I thinke thus: This candle did I light:
this light haue I kindeled: that learned men maie se, to practise their
pennes, their eloquence to aduaunce, to register their names in the
booke of memorie I drew the platte rudelie, whereon thei maie builde,
whom god hath indued with learning and liuelihod. For liuing by laboure
doth learning so hinder, that learning serueth liuinge, whiche is a
peruers trade. Yet as carefull familie shall cease hir cruell callinge,
and suffre anie laiser to learninge to repaire, I will not cease
from trauaile the pathe so to trade, that finer wittes maie fashion them
selues with such glimsinge dull light, a more complete woorke at
laiser to finisshe, with inuencion agreable, and aptnes of
eloquence.
xcvse me, gentle reder if oughte be amisse, straung paths ar not trodẽ
al truly at the first: the way muste needes be comberous, wher none
hathe gone before. Where no man hathe geuen light, lighte is it to
offend, but when the light is shewed ones, light is it to amende. If my
light may so light some other, to espie and marke my faultes,
I wish it may so lighten thẽ, that they may voide offence. Of
staggeringe and stomblinge, and vnconstaunt turmoilinge: often
offending, and seldome amending, such vices to eschewe, and their fine
wittes to shew that they may winne the praise, and I to hold the candle,
whilest they their glorious works with eloquence sette forth, so
cunningly inuented, so finely indited, that my bokes maie seme worthie
to occupie no roome. For neither is mi wit so finelie filed, nother mi
learning so largly lettred, nother yet mi laiser so quiet and vncõbered,
that I maie perform iustlie so learned a laboure or accordinglie to
accomplishe so
[§.ii.v]
haulte an enforcement, yet maie I thinke thus: This candle did I light:
this light haue I kindeled: that learned men maie se, to practise their
pennes, their eloquence to aduaunce, to register their names in the
booke of memorie I drew the platte rudelie, whereon thei maie builde,
whom god hath indued with learning and liuelihod. For liuing by laboure
doth learning so hinder, that learning serueth liuinge, whiche is a
peruers trade. Yet as carefull familie shall cease hir cruell callinge,
and suffre anie laiser to learninge to repaire, I will not cease
from trauaile the pathe so to trade, that finer wittes maie fashion them
selues with such glimsinge dull light, a more complete woorke at
laiser to finisshe, with inuencion agreable, and aptnes of
eloquence.
And this gentle reader I hartelie protest where erroure hathe happened I wisshe it redrest.
§.iij.
 t is not vnknowen to youre maiestie, moste soueraigne lorde, what great
disceptacion hath been amongest the wyttie men of all nacions, for the
exacte knoweledge of true felicitie, bothe what it is, and wherein it
consisteth: touchynge whiche thyng, their opinions almoste were as many
in numbre, as were the persons of them, that either disputed or wrote
thereof. But and if the diuersitie of opinions in the vulgar sort for
placyng of their felicitie shall be considered also, the varietie shall
be found so great, and the opinions so dissonant, yea plainly
monsterouse, that no honest witte would vouchesafe to lose time in
hearyng thẽ, or rather (as I may saie) no witte is of so exact
remembrance, that can consider together the monsterouse multitude of
them all. And yet not withstãdyng this repugnant diuersitie, in two
thynges do they all agree. First all do agre, that felicitie is and
ought to be the stop and end of all their doynges, so that he that hath
a full desire to any thyng how so euer it be estemed of other mẽ, yet he
estemeth him self happie, if he maie obtain it: and contrary waies
vnhappie if he can not attaine it. And therfore do all men put their
whole studie to gette that thyng, wherin they haue perswaded them self
that felicitie
[§.iii.v]
doth consist. Wherfore some whiche put their felicitie in fedyng their
bellies, thinke no pain to be hard, nor no dede to be vnhonest, that may
be a meanes to fill that foule panche. Other which put their felicitie
in play and ydle pastimes, iudge no time euill spent, that is employed
thereabout: nor no fraude vnlawfull that may further their winning. If I
should particularly ouerrũne but the common sortes of men, which put
their felicitie in their desires, it wold make a great boke of it self.
Therfore wyl I let them al go, and conclude as I began, That all men employ their whole
endeuour to that thing, wherin thei thinke felicitie to stand. whiche thyng who so
listeth to mark exactly, shall be able to espie and iudge the natures of
al men, whose conuersaciõ he doth know, though thei vse great
dissimulacion to colour their desires, especially whẽ they perceiue
other men to mislyke that which thei so much desire: For no mã wold
gladly haue his appetite improued. And herof cõmeth that secõnde thing
wherin al agree, that euery man would most gladly win all other men to
his sect, and to make thẽ of his opinion, and as far as he dare, will
dispraise all other mens iudgemẽtes, and praise his own waies only,
onles it be when he dissimuleth, and that for the furtherãce of his own
purpose. And this propertie also doth geue great light to the full
knowledge of mens natures, which as all men ought to obserue, so princes
aboue other haue most cause to mark for sundrie occasions which may lye
them on, wherof I shall not nede to speke any farther, consideryng not
only the greatnes of wit, and exactnes of iudgement whiche god hath lent
vnto your highnes person, but also ye most graue wisdom and
profoũd knowledge of your maiesties most honorable coũcel, by whõ your
highnes may so sufficiently vnderstãd all thinges conuenient, that lesse
shal it nede to vnderstand by priuate readying, but yet not vtterly to
refuse to read as often as occasion may serue, for bokes dare speake,
when men feare to displease. But to
[§.iiii.]
returne agayne to my firste matter, if none other good thing maie be
lerned at their maners, which so wrõgfully place their felicity, in so
miserable a cõditiõ (that while they thinke them selfes happy, their
felicitie must nedes seme vnluckie, to be by them so euill placed) yet
this may men learn at them, by those .ij. spectacles to espye the
secrete natures and dispositions of others, whiche thyng vnto a wise man
is muche auailable. And thus will I omit this great tablement of
vnhappie hap, and wil come to .iij. other sortes of a better degre,
wherof the one putteth felicitie to consist in power and royaltie. The
second sorte vnto power annexeth worldly wisdome, thinkyng him full
happie, that could attayn those two, wherby he might not onely haue
knowledge in all thynges, but also power to bryng his desires to ende.
The thyrd sort estemeth true felicitie to consist in wysdom annexed with
vertuouse maners, thinkyng that they can take harme of nothyng, if they
can with their wysedome* ouercome all vyces. Of the firste of those three sortes there hath
been a great numbre in all ages, yea many mightie kinges and great
gouernoures which cared not greately howe they myght atchieue their
pourpose, so that they dyd preuayle: nor did not take any greatter care
for gouernance, then to kepe the people in onely feare of them, Whose common
sentence was alwaies this: Oderint dum metuant. And what good
successe suche menne had, all histories doe report. Yet haue they not
wanted excuses: yea Iulius Cæsar (whiche in dede was of the second
sorte) maketh a kynde of excuse by his common sentence, for them of that
fyrste sorte, for he was euer woonte to saie: ἐίπερ γὰρ ἀδικεῖμ χρὴ, τυραννΐδος περῒ κάλλιστομ ἀδικεῖμ, τ’ ἄλλα
δ’ ἐυσεβεῖμ χρεῶμ. Whiche sentence I wysshe had neuer been
learned out of Grecia. But now to speake of the second sort, of whiche
there hathe been verye many also, yet for this present time amongest
them all, I wyll take the exaumples of
[§.iiii.v]
kynge Phylippe of Macedonie, and of Alexander his sonne, that valiaunt
conquerour. First of kinge Phylip it appeareth by his letter sente vnto
Aristotle that famous philosopher, that he more delited in the birthe of
his sonne, for the hope of learning and good education, that might
happen to him by the said Aristotle, then he didde reioyse in the
continuaunce of his succession, for these were his wordes and his whole
epistle, worthye to bee remembred and registred euery where.
t is not vnknowen to youre maiestie, moste soueraigne lorde, what great
disceptacion hath been amongest the wyttie men of all nacions, for the
exacte knoweledge of true felicitie, bothe what it is, and wherein it
consisteth: touchynge whiche thyng, their opinions almoste were as many
in numbre, as were the persons of them, that either disputed or wrote
thereof. But and if the diuersitie of opinions in the vulgar sort for
placyng of their felicitie shall be considered also, the varietie shall
be found so great, and the opinions so dissonant, yea plainly
monsterouse, that no honest witte would vouchesafe to lose time in
hearyng thẽ, or rather (as I may saie) no witte is of so exact
remembrance, that can consider together the monsterouse multitude of
them all. And yet not withstãdyng this repugnant diuersitie, in two
thynges do they all agree. First all do agre, that felicitie is and
ought to be the stop and end of all their doynges, so that he that hath
a full desire to any thyng how so euer it be estemed of other mẽ, yet he
estemeth him self happie, if he maie obtain it: and contrary waies
vnhappie if he can not attaine it. And therfore do all men put their
whole studie to gette that thyng, wherin they haue perswaded them self
that felicitie
[§.iii.v]
doth consist. Wherfore some whiche put their felicitie in fedyng their
bellies, thinke no pain to be hard, nor no dede to be vnhonest, that may
be a meanes to fill that foule panche. Other which put their felicitie
in play and ydle pastimes, iudge no time euill spent, that is employed
thereabout: nor no fraude vnlawfull that may further their winning. If I
should particularly ouerrũne but the common sortes of men, which put
their felicitie in their desires, it wold make a great boke of it self.
Therfore wyl I let them al go, and conclude as I began, That all men employ their whole
endeuour to that thing, wherin thei thinke felicitie to stand. whiche thyng who so
listeth to mark exactly, shall be able to espie and iudge the natures of
al men, whose conuersaciõ he doth know, though thei vse great
dissimulacion to colour their desires, especially whẽ they perceiue
other men to mislyke that which thei so much desire: For no mã wold
gladly haue his appetite improued. And herof cõmeth that secõnde thing
wherin al agree, that euery man would most gladly win all other men to
his sect, and to make thẽ of his opinion, and as far as he dare, will
dispraise all other mens iudgemẽtes, and praise his own waies only,
onles it be when he dissimuleth, and that for the furtherãce of his own
purpose. And this propertie also doth geue great light to the full
knowledge of mens natures, which as all men ought to obserue, so princes
aboue other haue most cause to mark for sundrie occasions which may lye
them on, wherof I shall not nede to speke any farther, consideryng not
only the greatnes of wit, and exactnes of iudgement whiche god hath lent
vnto your highnes person, but also ye most graue wisdom and
profoũd knowledge of your maiesties most honorable coũcel, by whõ your
highnes may so sufficiently vnderstãd all thinges conuenient, that lesse
shal it nede to vnderstand by priuate readying, but yet not vtterly to
refuse to read as often as occasion may serue, for bokes dare speake,
when men feare to displease. But to
[§.iiii.]
returne agayne to my firste matter, if none other good thing maie be
lerned at their maners, which so wrõgfully place their felicity, in so
miserable a cõditiõ (that while they thinke them selfes happy, their
felicitie must nedes seme vnluckie, to be by them so euill placed) yet
this may men learn at them, by those .ij. spectacles to espye the
secrete natures and dispositions of others, whiche thyng vnto a wise man
is muche auailable. And thus will I omit this great tablement of
vnhappie hap, and wil come to .iij. other sortes of a better degre,
wherof the one putteth felicitie to consist in power and royaltie. The
second sorte vnto power annexeth worldly wisdome, thinkyng him full
happie, that could attayn those two, wherby he might not onely haue
knowledge in all thynges, but also power to bryng his desires to ende.
The thyrd sort estemeth true felicitie to consist in wysdom annexed with
vertuouse maners, thinkyng that they can take harme of nothyng, if they
can with their wysedome* ouercome all vyces. Of the firste of those three sortes there hath
been a great numbre in all ages, yea many mightie kinges and great
gouernoures which cared not greately howe they myght atchieue their
pourpose, so that they dyd preuayle: nor did not take any greatter care
for gouernance, then to kepe the people in onely feare of them, Whose common
sentence was alwaies this: Oderint dum metuant. And what good
successe suche menne had, all histories doe report. Yet haue they not
wanted excuses: yea Iulius Cæsar (whiche in dede was of the second
sorte) maketh a kynde of excuse by his common sentence, for them of that
fyrste sorte, for he was euer woonte to saie: ἐίπερ γὰρ ἀδικεῖμ χρὴ, τυραννΐδος περῒ κάλλιστομ ἀδικεῖμ, τ’ ἄλλα
δ’ ἐυσεβεῖμ χρεῶμ. Whiche sentence I wysshe had neuer been
learned out of Grecia. But now to speake of the second sort, of whiche
there hathe been verye many also, yet for this present time amongest
them all, I wyll take the exaumples of
[§.iiii.v]
kynge Phylippe of Macedonie, and of Alexander his sonne, that valiaunt
conquerour. First of kinge Phylip it appeareth by his letter sente vnto
Aristotle that famous philosopher, that he more delited in the birthe of
his sonne, for the hope of learning and good education, that might
happen to him by the said Aristotle, then he didde reioyse in the
continuaunce of his succession, for these were his wordes and his whole
epistle, worthye to bee remembred and registred euery where.
Φΐλιππος Αριστοτέλει χαίρειμ.
ἔσθι μοι γεγονότα ὑομ. πολλὴμ οὖμ τοῖσ θεοῖσ χάριμ ἔχω, ὀυχ ὅυτωσ ἐπῒ τῆ γεννήσει του παιδόσ, ὡσ ἐπῒ τῷ κατὰ τὴμ σὴμ ἡλικῒαμ αὐτόμ γεγονέναι ἐλπΐζω γὰρ αὐτὸμ ὑπὸ σοῦ γραφέντα καὶ παιδευθέντα ἄξιομ ἔσεσθαι καὶ ἑιμῶμ καὶ τῆς τῶμ τραγμάτωμ διαδοχῆσ.
That is thus in sense,
Philip vnto Aristotle sendeth gretyng.
You shall vnderstande, that I haue a sonne borne, for whiche cause I yelde vnto God moste hartie thankes, not so muche for the byrthe of the childe, as that it was his chaunce to be borne in your tyme. For my trust is, that he shall be so brought vp and instructed by you, that he shall become worthie not only to be named our sonne, but also to be the successour of our affayres.
And his good desire was not all vayne, for it appered that Alexander was neuer so busied with warres (yet was he neuer out of moste terrible battaile) but that in the middes thereof he had in remembraunce his studies, and caused in all countreies as he went, all strange beastes, ⁊.i. fowles and fisshes, to be taken and kept for the ayd of that knowledg, which he learned of Aristotle: And also to be had with him alwayes a greate numbre of learned men. And in the moste busye tyme of all his warres against Darius kinge of Persia, when he harde that Aristotle had putte forthe certaine bookes of suche knowledge wherein he hadde before studied, hee was offended with Aristotle, and wrote to hym this letter.
Ἄλέζανδρος Αρισοτέλει εὖ πράττειμ.
Ὂυκ ὀρθῶσ ἐπόιησασ ἐκδοὺσ τοὺσ ἀκροαματικόυσ τῶμ λόγωμ,τΐνι γὰρ διοισομην ἡμεῖσ τῶμ ἄλλωμ, ἐι καθ’ οὕσ ἐπαιδεύθημεν λόγουσ, ὅυτοι πάντωμ ἔσονταιν κοινόι, ἐγὼ δὲ βουλοί μημ ἅμ ταῖσ περι τὰ ἄριστα ἐμπειρΐαισ, ἢ τὰισ δυνάμεσι διαφέριμ. ἔρρωσο. that is
Alexander vnto Aristotle sendeth greeting.
You haue not doone well, to put forthe those bookes of secrete phylosophy intituled, ακροαματικοι. For wherin shall we excell other, yf that knowledge that wee haue studied, shall be made commen to all other men, namely sithe our desire is to excelle other men in experience and knowledge, rather then in power and strength. Farewell.
By whyche lettre it appeareth that hee estemed learninge and knowledge aboue power of men. And the like iudgement did he vtter, when he beheld the state of Diogenes Linicus, adiudginge it the beste state next to his owne, so that he said: If I were not Alexander, I wolde wishe to be Diogenes. Whereby apeareth, how he esteemed learning, and what felicity he putte therin, reputing al the worlde saue him selfe to be inferiour to Diogenes. And bi al coniecturs, Alexander did esteme Diogenes one of them whiche contemned the vaine estimation of the disceitfull world, and put his whole felicity in knowledg of vertue, and practise of the same, though some reporte [⁊.i.v] that he knew more vertue then he folowed: But whatso euer he was, it appeareth that Socrates and Plato and many other did forsake their liuings and sel away their patrimony, to the intent to seeke and trauaile for learning, which examples I shall not need to repete to your Maiesty, partly for that your highnes doth often reade them and other lyke, and partly sith your maiesty hath at hand such learned schoolemaysters, which can much better thẽ I, declare them vnto your highnes, and that more largely also then the shortenes of thys epistle will permit. But thys may I yet adde, that King Salomon whose renoume spred so farre abroad, was very greatlye estemed for his wonderfull power and exceading treasure, but yet much more was he estemed for his wisdom. And him selfe doth bear witnes, that wisedom is better then pretious stones . yea all thinges that can be desired ar not to be compared to it. But what needeth to alledge one sentence of him, whose bookes altogither do none other thing, then set forth the praise of wisedom & knowledg? And his father king Dauid ioyneth uertuous conuersacion and knowledg togither, as the summe of perfection and chief felicity. Wherfore I maye iustelye conclude, that true felicity doth consist in wisdome and vertu. Then if wisdome be as Cicero defineth it, Diuinarum atq; humanarum rerum scientia, then ought all men to trauail for knowledg in matters both of religion and humaine docrine, if he shall be counted wyse, and able to attaine true felicitie: But as the study of religious matters is most principall, so I leue it for this time to them that better can write of it then I can. And for humaine knowledge thys wil I boldly say, that who soeuer wyll attain true iudgment therein, must not only trauail in ye knowledg of the tungs, but must also before al other arts, taste of the mathematical sciences, specially Arithmetike and Geometry, without which it is not possible to attayn full knowledg in any art. Which may sufficiẽtly by gathered by Aristotle not õly in his bookes ⁊.ii. of demonstration (whiche can not be vnderstand without Geometry) but also in all his other workes. And before him Plato his maister wrote this sentence on his schole house dore. Αγεομέτρητοσ ὀυδὲισ ἐισΐτω.. Let no man entre here (saith he) without knowledg in Geometry. Wherfore moste mighty prince, as your most excellent Maiesty appeareth to be borne vnto most perfect felicity, not only by reasõ that God moued with the long prayers of this realme, did send your highnes as moste comfortable inheritour to the same, but also in that your Maiesty was borne in the time of such skilful schoolmaisters & learned techers, as your highnes doth not a little reioyse in, and profite by them in all kind of vertu & knowledg. Amõgst which is that heauẽly knowledg most worthely to be praised, wherbi the blindnes of errour & superstition is exiled, & good hope cõceiued that al the sedes & fruts therof, with all kindes of vice & iniquite, wherby vertu is hindered, & iustice defaced, shal be clean extrirped and rooted out of this realm, which hope shal increase more and more, if it may appear that learning be estemed & florish within this realm. And al be it the chief learnĩg be the diuine scriptures, which instruct the mind principally, & nexte therto the lawes politike, which most specially defẽd the right of goodes, yet is it not possible that those two can long be wel vsed, if that ayde want that gouerneth health and expelleth sicknes, which thing is done by Physik, & these require the help of the vij. liberall sciences, but of none more then of Arithmetik and Geometry, by which not only great thinges ar wrought touchĩg accõptes in al kinds, & in suruaiyng & measuring of lãdes, but also al arts depend partly of thẽ, & building which is most necessary can not be wtout them, which thing cõsidering, moued me to help to serue your maiesty in this point as wel as other wais, & to do what mai be in me, yt not õly thei which studi prĩcipalli for lernĩg, mai haue furderãce bi mi poore help, but [⁊.ii.v] also those whiche haue no tyme to trauaile for exacter knowlege, may haue some helpe to vnderstand in those Mathematicall artes, in whiche as I haue all readye set forth sumwhat of Arithmetike, so god willing I intend shortly to setforth a more exacter worke therof. And in the meane ceason for a taste of Geometry, I haue sette forthe this small introduction, desiring your grace not so muche to beholde the simplenes of the woorke, in comparison to your Maiesties excellencye, as to fauour the edition thereof, for the ayde of your humble subiectes, which shal thinke them selues more and more dayly bounden to your highnes, if when they shall perceaue your graces desyre to haue theym profited in all knowledge and vertue. And I for my poore ability considering your Maiesties studye for the increase of learning generally through all your highenes dominions, and namely in the vniuersities of Oxforde and Camebridge, as I haue an earnest good will as far as my simple seruice and small knowledg will suffice, to helpe toward the satisfiyng of your graces desire, so if I shall perceaue that my seruice may be to your maiesties contẽtacion, I wil not only put forth the other two books, whiche shoulde haue beene sette forth with these two, yf misfortune had not hindered it, but also I wil set forth other bookes of more exacter arte, bothe in the Latine tongue and also in the Englyshe, whereof parte bee all readye written, and newe instrumentes to theym deuised, and the residue shall bee eanded with all possible speede. I was boldened to dedicate this booke of Geometrye vnto your Maiestye, not so muche bycause it is the firste that euer was sette forthe in Englishe, and therefore for the noueltye a straunge presente, but for that I was perswaded, that suche a wyse prince doothe desire to haue a wise sorte of subiectes. For it is a kynges chiefe reioysinge and glory, if his subiectes be riche in substaunce, and wytty in knowledge: and contrarye ⁊.iii. waies nothyng can bee more greuouse to a noble kyng, then that his realme should be other beggerly or full of ignoraunce: But as god hath geuen your grace a realme bothe riche in commodities and also full of wyttie men, so I truste by the readyng of wyttie artes (whiche be as the whette stones of witte) they muste needes increase more and more in wysedome, and peraduenture fynde some thynge towarde the ayde of their substaunce, whereby your grace shall haue newe occasion to reioyce, seyng your subiectes to increase in substance or wisdom, or in both. And thei again shal haue new and new causes to pray for your maiestie, perceiuyng so graciouse a mind towarde their benefite. And I truste (as I desire) that a great numbre of gentlemen, especially about the courte, whiche vnderstand not the latin tong, or els for the hardnesse of the mater could not away with other mens writyng, will fall in trade with this easie forme of teachyng in their vulgar tong, and so employe some of their tyme in honest studie, whiche were wont to bestowe most part of their time in triflyng pastime: For vndoubtedly if they mean other your maiesties seruice, other their own wisdome, they will be content to employ some tyme aboute this honest and wittie exercise. For whose encouragemẽt to the intent they maie perceiue what shall be the vse of this science, I haue not onely written somewhat of the vse of Geometrie, but also I haue annexed to this boke the names and brefe argumentes of those other bokes whiche I will set forth hereafter, and that as shortly as it shall appeare vnto your maiestie by coniecture of their diligent vsyng of this first boke, that they wyll vse well the other bokes also. In the meane ceason, and at all times I wil be a continuall petitioner, that god may work in all english hartes an ernest mynde to all honest exercises, wherby thei may serue the better your maiestie and [⁊.iii.v] the realm. And for your highnes I besech the most mercifull god, as he hath most fauourably sent you vnto vs, as our chefe comforter in earthe, so that he will increase your maiestie daiely in all vertue and honor with moste prosperouse successe, and augment in vs your most humble subiectes, true loue to godward, and iust obedience toward your highnes with all reuerence and subiection.
At London the .xxviij. daie of Ianuarie. M. D. L I.
Your maiesties moste humble seruant
and obedient subiect,
Robert Recorde.
THE PREFACE,
declaring briefely the commodi-
tes of Geometrye, and the
necessitye thereof.
 Eometrye may thinke it selfe to sustaine great iniury, if it shall be
inforced other to show her manifold commodities, or els not to prease
into the sight of men, and therefore might this wayes answere briefely:
Other I am able to do you much good, or els but litle. If I bee able to
doo you much good, then be you not your owne friendes, but greatlye your
owne enemies to make so little of me, which maye profite you so muche.
For if I were as vncurteous as you vnkind, I shuld vtterly refuse
to do them any good, which will so curiously put me to the trial and
profe of my commodities, or els to suffre exile, and namely sithe I shal
only yeld benefites to other, and receaue none againe. But and if you
could saye truely, that my benefites be nother many nor yet greate, yet
if they bee anye, I doo yelde more to you, then I doo receaue
againe of you, and therefore I oughte not to bee repelled of them that
loue them selfe, althoughe they loue me not all for my selfe. But as I
am in nature a liberall science, so canne I not againste nature contende
with your inhumanitye, but muste shewe my selfe liberall euen to myne
enemies. Yet this is my comforte againe, that I haue none enemies but
them that knowe me not, and therefore may hurte themselues, but can not
noye me. Yf they dispraise the thinge that they know not, all wise men
will blame them and not credite them, and yf they thinke they knowe me,
lette theym shewe one vntruthe and erroure in me, and I wyll geue the
victorye.
Eometrye may thinke it selfe to sustaine great iniury, if it shall be
inforced other to show her manifold commodities, or els not to prease
into the sight of men, and therefore might this wayes answere briefely:
Other I am able to do you much good, or els but litle. If I bee able to
doo you much good, then be you not your owne friendes, but greatlye your
owne enemies to make so little of me, which maye profite you so muche.
For if I were as vncurteous as you vnkind, I shuld vtterly refuse
to do them any good, which will so curiously put me to the trial and
profe of my commodities, or els to suffre exile, and namely sithe I shal
only yeld benefites to other, and receaue none againe. But and if you
could saye truely, that my benefites be nother many nor yet greate, yet
if they bee anye, I doo yelde more to you, then I doo receaue
againe of you, and therefore I oughte not to bee repelled of them that
loue them selfe, althoughe they loue me not all for my selfe. But as I
am in nature a liberall science, so canne I not againste nature contende
with your inhumanitye, but muste shewe my selfe liberall euen to myne
enemies. Yet this is my comforte againe, that I haue none enemies but
them that knowe me not, and therefore may hurte themselues, but can not
noye me. Yf they dispraise the thinge that they know not, all wise men
will blame them and not credite them, and yf they thinke they knowe me,
lette theym shewe one vntruthe and erroure in me, and I wyll geue the
victorye.
Yet can no humayne science saie thus, but I onely, that there is no sparke of vntruthe in me: but all my doctrine and workes are without any blemishe of errour that mans reason can discerne. And nexte vnto me in certaintie are my three systers, Arithmetike, Musike, and Astronomie, whiche are also so nere knitte in amitee, that he that loueth the one, can not despise the other, and in especiall Geometrie, of whiche not only these thre, but all other artes do borow great ayde, as partly hereafter shall be shewed. But first will I beginne with the vnlearned sorte, that you maie perceiue how that no arte can stand without me. For if I should declare how many wayes my helpe is vsed, in measuryng of ground, for medow, corne, and wodde: in hedgyng, in dichyng, and in stackes makyng, I thinke the poore Husband man would be more thankefull vnto me, then he is nowe, whyles he thinketh that he hath small benefite by me. Yet this maie he coniecture certainly, that if he kepe not the rules of Geometrie, he can not measure any ground truely. And in dichyng, if he kepe not a proportion of bredth in the mouthe, to the bredthe of the bottome, and iuste slopenesse in the sides agreable to them bothe, the diche shall be faultie many waies. When he doth make stackes for corne, or for heye, he practiseth good Geometrie, els would thei not long stand: So that in some stakes, whiche stand on foure pillers, and yet made round, doe increase greatter and greatter a good height, and then againe turne smaller and smaller vnto the toppe: you maie see so good Geometrie, that it were very difficult to counterfaite the lyke in any kynde of buildyng. As for other infinite waies that he vseth my benefite, I ouerpasse for shortnesse.
Carpenters, Karuers, Ioyners, and Masons, doe willingly acknowledge that they can worke nothyng without reason of Geometrie, in so muche that they chalenge me as a peculiare science for them. But in that they should do wrong to all other men, seyng euerie kynde of men haue som benefit by me, not only in buildyng, whiche is but other mennes costes, and the arte of Carpenters, Masons, and the other aforesayd, but in their †.i. owne priuate profession, whereof to auoide tediousnes I make this rehersall.
Sith Merchauntes by shippes great riches do winne,
I may with good righte at their seate beginne.
The Shippes on the sea with Saile and with Ore,
were firste founde, and styll made, by Geometries lore.
Their Compas, their Carde, their Pulleis, their Ankers,
were founde by the skill of witty Geometers.
To sette forth the Capstocke, and eche other parte,
wold make a greate showe of Geometries arte.
Carpenters, Caruers, Ioiners and Masons,
Painters and Limners with suche occupations,
Broderers, Goldesmithes, if they be cunning,
Must yelde to Geometrye thankes for their learning.
The Carte and the Plowe, who doth them well marke,
Are made by good Geometrye. And so in the warke
Of Tailers and Shoomakers, in all shapes and fashion,
The woorke is not praised, if it wante proportion.
So weauers by Geometrye hade their foundacion,
Their Loome is a frame of straunge imaginacion.
The wheele that doth spinne, the stone that doth grind,
The Myll that is driuen by water or winde,
Are workes of Geometrye straunge in their trade,
Fewe could them deuise, if they were vnmade.
And all that is wrought by waight or by measure,
without proofe of Geometry can neuer be sure.
Clockes that be made the times to deuide,
The wittiest inuencion that euer was spied,
Nowe that they are common they are not regarded,
The artes man contemned, the woorke vnrewarded.
But if they were scarse, and one for a shewe,
Made by Geometrye, then shoulde men know,
That neuer was arte so wonderfull witty,
So needefull to man, as is good Geometry.
The firste findinge out of euery good arte,
Seemed then vnto men so godly a parte,
[†.i.v]That no recompence might satisfye the finder,
But to make him a god, and honoure him for euer.
So Ceres and Pallas, and Mercury also,
Eolus and Neptune, and many other mo,
Were honoured as goddes, bicause they did teache,
Firste tillage and weuinge and eloquent speache,
Or windes to obserue, the seas to saile ouer,
They were called goddes for their good indeuour.
Then were men more thankefull in that golden age:
This yron wolde nowe vngratefull in rage,
Wyll yelde the thy reward for trauaile and paine,
With sclaunderous reproch, and spitefull disdaine.
Yet thoughe other men vnthankfull will be,
Suruayers haue cause to make muche of me.
And so haue all Lordes, that landes do possesse:
But Tennaunted I feare will like me the lesse.
Yet do I not wrong but measure all truely,
All yelde the full right of euerye man iustely.
Proportion Geometricall hath no man opprest,
Yf anye bee wronged, I wishe it redrest.
But now to procede with learned professions, in Logike and Rhetorike and all partes of phylosophy, there neadeth none other proofe then Aristotle his testimony, whiche without Geometry proueth almost nothinge. In Logike all his good syllogismes and demonstrations, hee declareth by the principles of Geometrye. In philosophye, nether motion, nor time, nor ayrye impressions could hee aptely declare, but by the helpe of Geometrye as his woorkes do witnes. Yea the faculties of the minde dothe hee expresse by similitude to figures of Geometrye. And in morall phylosophy he thought that iustice coulde not wel be taught, nor yet well executed without proportion geometricall. And this estimacion of Geometry he maye seeme to haue learned of his maister Plato, which without Geometrye wolde teache nothinge, nother wold admitte any to heare him, except he were experte in Geometry. And what merualle if he so muche estemed geometrye, seinge his opinion was, that Godde was alwaies workinge [†].ii. by Geometrie? Whiche sentence Plutarche declareth at large. And although Platto do vse the helpe of Geometrye in all the most waighte matter of a common wealth, yet it is so generall in vse, that no small thinges almost can be wel done without it. And therfore saith he: that Geometrye is to be learned, if it were for none other cause, but that all other artes are bothe soner and more surely vnderstand by helpe of it.
What greate help it dothe in physike, Galene doth so often and so copiousely declare, that no man whiche hath redde any booke almoste of his, can be ignorant thereof, in so much that he coulde neuer cure well a rounde vlcere, tyll reason geometricall dydde teache it hym. Hippocrates is earnest in admonyshynge that study of geometrie must prepare the way to physike, as well as to all other artes.
I shoulde seeme somewhat to tedious, if I shoulde recken vp, howe the diuines also in all their mysteries of scripture doo vse healpe of geometrie: and also that lawyers can neuer vnderstande the hole lawe, no nor yet the firste title therof exactly without Geometrie. For if lawes can not well be established, nor iustice duelie executed without geometricall proportion, as bothe Plato in his Politike bokes, and Aristotle in his Moralles doo largely declare. Yea sithe Lycurgus that cheefe lawmaker amongest the Lacedemonians, is moste praised for that he didde chaunge the state of their common wealthe frome the proportion Arithmeticall to a proportion geometricall, whiche without knowledg of bothe he coulde not dooe, than is it easye to perceaue howe necessarie Geometrie is for the lawe and studentes thereof. And if I shall saie preciselie and freelie as I thinke, he is vtterlie destitute of all abilitee to iudge in anie arte, that is not sommewhat experte in the Theoremes of Geometrie.
And that caused Galene to say of hym selfe, that he coulde neuer perceaue what a demonstration was, no not so muche, as whether there were any or none, tyll he had by geometrie gotten abilitee to vnderstande it, although he heard the beste teachers that were in his tyme. It shuld be to longe and nedelesse [†.ii.v] also to declare what helpe all other artes Mathematicall haue by geometrie, sith it is the grounde of all theyr certeintie, and no man studious in them is so doubtful therof, that he shall nede any persuasion to procure credite thereto. For he can not reade .ij. lines almoste in any mathematicall science, but he shall espie the nedefulnes of geometrie. But to auoyde tediousnesse I will make an ende hereof with that famous sentence of auncient Pythagoras, That who so will trauayle by learnyng to attayne wysedome, shall neuer approche to any excellencie without the artes mathematicall, and especially Arithmetike and Geometrie.
And yf I shall somewhat speake of noble men, and gouernours of realmes, howe needefull Geometrye maye bee vnto them, then must I repete all that I haue sayde before, sithe in them ought all knowledge to abounde, namely that maye appertaine either to good gouernaunce in time of peace, eyther wittye pollicies in time of warre. For ministration of good lawes in time of peace Lycurgus example with the testimonies of Plato and Aristotle may suffise. And as for warres, I might thinke it sufficient that Vegetius hath written, and after him Valturius in commendation of Geometry, for vse of warres, but all their woordes seeme to saye nothinge, in comparison to the example of Archimedes worthy woorkes make by geometrie, for the defence of his countrey, to reade the wonderfull praise of his wittie deuises, set foorthe by the most famous hystories of Liuius, Plutarche, and Plinie, and all other hystoriographiers, whyche wryte of the stronge siege of Syracusæ made by that valiant capitayne, and noble warriour Marcellus, whose power was so great, that all men meruayled how that one citee coulde withstande his wonderfull force so longe. But much more woulde they meruaile, if they vnderstode that one man onely dyd withstand all Marcellus strength, and with counter engines destroied his engines to the vtter astonyshment of Marcellus, and all that were with hym. He had inuented suche balastelas that dyd shoote out a hundred dartes at one †.iij. shotte, to the great destruction of Marcellus souldiours, wherby a fonde tale was spredde abrode, how that in Syracusæ there was a wonderfull gyant, whiche had a hundred handes, and coulde shoote a hundred dartes at ones. And as this fable was spredde of Archimedes, so many other haue been fayned to bee gyantes and monsters, bycause they dyd suche thynges, whiche farre passed the witte of the common people. So dyd they feyne Argus to haue a hundred eies, bicause they herde of his wonderfull circumspection, and thoughte that as it was aboue their capacitee, so it could not be, onlesse he had a hundred eies. So imagined they Ianus to haue two faces, one lokyng forwarde, and an other backwarde, bycause he coulde so wittily compare thynges paste with thynges that were to come, and so duely pondre them, as yf they were all present. Of like reasõ did they feyn Lynceus to haue such sharp syght, that he could see through walles and hylles, bycause peraduenture he dyd by naturall iudgement declare what cõmoditees myght be digged out of the grounde. And an infinite noumbre lyke fables are there, whiche sprange all of lyke reason.
For what other thyng meaneth the fable of the great gyant Atlas, whiche was ymagined to beare vp heauen on his shulders? but that he was a man of so high a witte, that it reached vnto the skye, and was so skylfull in Astronomie, and coulde tell before hande of Eclipses, and other like thynges as truely as though he dyd rule the sterres, and gouerne the planettes.
So was Eolus accompted god of the wyndes, and to haue theim all in a caue at his pleasure, by reason that he was a wittie man in naturall knowlege, and obserued well the change of wethers, aud was the fyrst that taught the obseruation of the wyndes. And lyke reson is to be geuen of al the old fables.
But to retourne agayne to Archimedes, he dyd also by arte perspectiue (whiche is a parte of geometrie) deuise such glasses within the towne of Syracusæ, that dyd bourne their ennemies shyppes a great way from the towne, whyche was a meruaylous politike thynge. And if I shulde repete the [†.iii.v] varietees of suche straunge inuentions, as Archimedes and others haue wrought by geometrie, I should not onely excede the order of a preface, but I should also speake of suche thynges as can not well be vnderstande in talke, without somme knowledge in the principles of geometrie.
But this will I promyse, that if I may perceaue my paynes to be thankfully taken, I wyll not onely write of suche pleasant inuentions, declaryng what they were, but also wil teache howe a great numbre of them were wroughte, that they may be practised in this tyme also. Wherby shallbe plainly perceaued, that many thynges seme impossible to be done, whiche by arte may very well be wrought. And whan they be wrought, and the reason therof not vnderstande, than say the vulgare people, that those thynges are done by negromancy. And hereof came it that fryer Bakon was accompted so greate a negromancier, whiche neuer vsed that arte (by any coniecture that I can fynde) but was in geometrie and other mathematicall sciences so experte, that he coulde dooe by theim suche thynges as were wonderfull in the syght of most people.
Great talke there is of a glasse that he made in Oxforde, in whiche men myght see thynges that were doon in other places, and that was iudged to be done by power of euyll spirites. But I knowe the reason of it to bee good and naturall, and to be wrought by geometrie (sythe perspectiue is a parte of it) and to stande as well with reason as to see your face in cõmon glasse. But this conclusion and other dyuers of lyke sorte, are more mete for princes, for sundry causes, than for other men, and ought not to bee taught commonly. Yet to repete it, I thought good for this cause, that the worthynes of geometry myght the better be knowen, & partly vnderstanding geuen, what wonderfull thynges may be wrought by it, and so consequently how pleasant it is, and how necessary also.
And thus for this tyme I make an end. The reason of som thynges done in this boke, or omitted in the same, you shall fynde in the preface before the Theoremes.*
The definitions of the principles of
GEOMETRY.
 eometry teacheth the drawyng, Measuring and proporcion of figures. but in as muche as no figure
can bee drawen, but it muste haue certayne boũdes and inclosures of
lines: and euery lyne also is begon and ended at some certaine prycke,
fyrst it shal be meete to know these smaller partes of euery figure,
that therby the whole figures may the better bee iudged, and distincte
in sonder.
eometry teacheth the drawyng, Measuring and proporcion of figures. but in as muche as no figure
can bee drawen, but it muste haue certayne boũdes and inclosures of
lines: and euery lyne also is begon and ended at some certaine prycke,
fyrst it shal be meete to know these smaller partes of euery figure,
that therby the whole figures may the better bee iudged, and distincte
in sonder.
A poincte. A Poynt or a Prycke, is named of Geometricians that small and vnsensible shape, whiche hath in it no partes, that is to say: nother length, breadth nor depth. But as their exactnes of definition is more meeter for onlye Theorike speculacion, then for practise and outwarde worke (consideringe that myne intent is to applye all these whole principles to woorke) I thynke meeter for this purpose, to call a poynt or prycke, that small printe of penne, pencyle, or other instrumente, whiche is not moued, nor drawen from his fyrst touche, and therfore hath no notable length nor bredthe: as this example doeth declare. ∴
Where I haue set .iij. prickes, eche of them hauyng both lẽgth and bredth, thogh it be but smal, and thefore not notable.
Nowe of a great numbre of these prickes, is made a Lyne, as you may perceiue by this forme ensuyng. ············ where as I haue set a numbre of prickes, so if you with your pen will set in more other prickes betweene euerye two of these, A lyne. then wil it be a lyne, as here you may see and this lyne, is called of Geometricians, Lengthe withoute breadth.
But as they in theyr theorikes (which ar only mind workes) [A.i.v] do precisely vnderstand these definitions, so it shal be sufficient for those men, whiche seke the vse of the same thinges, as sense may duely iudge them, and applye to handy workes if they vnderstand them so to be true, that outwarde sense canne fynde none erroure therein.
Of lynes there bee two principall kyndes. The one is called a right or straight lyne, and the other a croked lyne.
A streghte lyne. A Straight lyne, is the shortest that maye be drawenne between two prickes.
A crokyd lyne. And all other lines, that go not right forth from prick to prick, but boweth any waye, such are called Croked lynes as in these examples folowyng ye may se, where I haue set but one forme of a straight lyne, for more formes there be not, but of crooked lynes there bee innumerable diuersities, whereof for examples sum I haue sette here.
![]() A right lyne.
A right lyne.
| Croked lynes. | ||
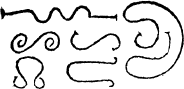 Croked lines. |
 |
 |
So now you must vnderstand, that euery lyne is drawen betwene twoo prickes, wherof the one is at the beginning, and the other at the ende.
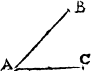
Therefore when soeuer you do see any formes of lynes to touche at one notable pricke, as in this example, then shall you A ij not call it one croked lyne, but rather twoo lynes: an Angle. in as muche as there is a notable and sensible angle by .A. whiche euermore is made by the meetyng of two seuerall lynes. And likewayes shall you iudge of this figure, whiche is made of two lines, and not of one onely.
![]()
So that whan so euer any suche meetyng of lines doth happen, the place of their metyng is called an Angle or corner.
Of angles there be three generall kindes: a sharpe angle, a square angle, and a blunte angle. A righte angle. The square angle, whiche is commonly named a right corner, is made of twoo lynes meetyng together in fourme of a squire, whiche two lines, if they be drawen forth in length, will crosse one an other: as in the examples folowyng you maie see.
Right angles.
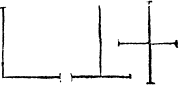
A sharpe corner. A sharpe angle is so called, because it is lesser than is a square angle, and the lines that make it, do not open so wide in their departynge as in a square corner, and if thei be drawen crosse, all fower corners will not be equall.
A blunte angle. A blunt or brode corner, is greater then is a square angle, and his lines do parte more in sonder then in a right angle, of whiche all take these examples.
And these angles (as you see) are made partly of streght lynes, partly of croken lines, and partly of both together. Howbeit in right angles I haue put none example of croked lines, because it would [A.ii.v] muche trouble a lerner to iudge them: for their true iudgment doth appertaine to arte perspectiue, and as I may say, rather to reason then to sense.
Sharpe angles.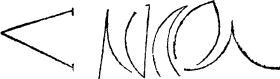 |
Blunte or brode angles. |
But now as of many prickes there is made one line, so of diuerse lines are there made sundry formes, figures, and shapes, whiche all yet be called by one propre name, A platte forme. Platte formes, and thei haue bothe length and bredth, but yet no depenesse.
And the boundes of euerie platte forme are lines: as by the examples you maie perceiue.
Of platte formes some be plain, and some be croked, and some parly plaine, and partlie croked.
A plaine platte. A plaine platte is that, whiche is made al equall in height, so that the middle partes nother bulke vp, nother shrink down more then the bothe endes.
A crooked platte. For whan the one parte is higher then the other, then is it named a Croked platte.
And if it be partlie plaine, and partlie crooked, then is it called a Myxte platte, of all whiche, these are exaumples.
| A plaine platte. | A croked platte. | A myxte platte. |
 |
 |
 |
And as of many prickes is made a line, and of diuerse lines one platte forme, A bodie. so of manie plattes is made a bodie, whiche conteigneth Lengthe, bredth, and depenesse. Depenesse. By Depenesse I vnderstand, not as the common sort doth, the holownesse of any thing, as of a well, a diche, a potte, and suche like, but I meane the massie thicknesse A iii of any bodie, as in exaumple of a potte: the depenesse is after the common name, the space from his brimme to his bottome. But as I take it here, the depenesse of his bodie is his thicknesse in the sides, whiche is an other thyng cleane different from the depenesse of his holownes, that the common people meaneth.
Now all bodies haue platte formes for their boundes, Cubike. so in a dye (whiche is called a cubike bodie) by geomatricians, Asheler. and an ashler of masons, there are .vi. sides, whiche are .vi. platte formes, and are the boundes of the dye.
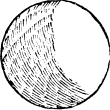
A globe. But in a Globe, (whiche is a bodie rounde as a bowle) there is but one platte forme, and one bounde, and these are the exaumples of them bothe.
| A dye or ashler. | A globe. |
 |
 |
But because you shall not muse what I dooe call a bound, A bounde. I mean therby a generall name, betokening the beginning, end and side, of any forme.
Forme, Fygure. A forme, figure, or shape, is that thyng that is inclosed within one bond or manie bondes, so that you vnderstand that shape, that the eye doth discerne, and not the substance of the bodie.
Of figures there be manie sortes, for either thei be made of prickes, lines, or platte formes. Not withstandyng to speake properlie, a figure is euer made by platte formes, and not of bare lines vnclosed, neither yet of prickes.
Yet for the lighter forme of teachyng, it shall not be vnsemely to call all suche shapes, formes and figures, whiche ye eye maie discerne distinctly.
And first to begin with prickes, there maie be made diuerse formes of them, as partely here doeth folowe.
[A.iii.v]| A lynearic numbre. | |
| Trianguler numbres | |
| Longsquare nũbre. | |
| Iust square numbres | |
| a threcornered spire. | |
| A square spire. |
And so maie there be infinite formes more, whiche I omitte for this time, cõsidering that their knowledg appertaineth more to Arithmetike figurall, than to Geometrie.
But yet one name of a pricke, whiche he taketh rather of his place then of his fourme, maie I not ouerpasse. And that is, when a pricke standeth in the middell of a circle (as no circle can be made by cõpasse without it) then is it called a centre. A centre And thereof doe masons, and other worke menne call that patron, a centre, whereby thei drawe the lines, for iust hewyng of stones for arches, vaultes, and chimneies, because the chefe vse of that patron is wrought by findyng that pricke or centre, from whiche all the lynes are drawen, as in the thirde booke it doeth appere.
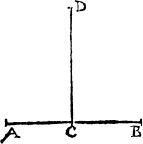
Lynes make diuerse figures also, though properly thei maie not be called figures, as I said before (vnles the lines do close) but onely for easie maner of teachyng, all shall be called [A.iiii.] figures, that the eye can discerne, of whiche this is one, when one line lyeth flatte (whiche is named A ground line. the ground line) and an other commeth downe on it, and is called A perpendicular. A plume lyne. a perpendiculer or plũme lyne, as in this example you may see. where .A.B. is the grounde line, and C.D. the plumbe line.
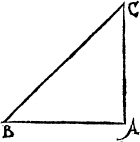
And like waies in this figure there are three lines, the grounde lyne whiche is A.B. the plumme line that is A.C. and the bias line, whiche goeth from the one of thẽ to the other, and lieth against the right corner in such a figure whiche is here .C.B.
But consideryng that I shall haue occasion to declare sundry figures anon, I will first shew some certaine varietees of lines that close no figures, but are bare lynes, and of the other lines will I make mencion in the description of the figures.

Parallelys Gemowe lynes. Paralleles, or gemowe lynes be suche lines as be drawen foorth still in one distaunce, and are no nerer in one place then in an other, for and if they be nerer at one ende then at the other, then are they no paralleles, but maie bee called bought lynes, and loe here exaumples of them bothe.
[A.iiii.v]| parallelis. | bought lines |
| parallelis: circular. Concen- trikes. |
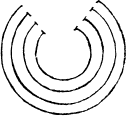 |
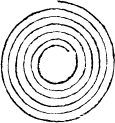
I haue added also paralleles tortuouse, whiche bowe cõtrarie waies with their two endes: and paralleles circular, whiche be lyke vnperfecte compasses: for if they bee whole circles, Concentrikes then are they called cõcentrikes, that is to saie, circles drawẽ on one centre.
Here might I note the error of good Albert Durer, which affirmeth that no perpendicular lines can be paralleles. which errour doeth spring partlie of ouersight of the difference of a streight line, and partlie of mistakyng certain principles geometrical, which al I wil let passe vntil an other tyme, and wil not blame him, which hath deserued worthyly infinite praise.
And to returne to my matter. A twine line. an other fashioned line is there, which is named a twine or twist line, and it goeth as a wreyth about some other bodie. A spirall line. And an other sorte of lines is there, that is called a spirall line, A worme line. or a worm line, whiche representeth an apparant forme of many circles, where there is not one in dede: of these .ii. kindes of lines, these be examples.
| A twiste lyne. |
 |
A spirail lyne |
 |
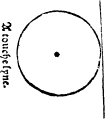
A touche lyne, is a line that runneth a long by the edge of a circle, onely touching it, but doth not crosse the circumference of it, as in this exaumple you maie see.
A corde,And when that a line doth crosse the edg of the circle, thẽ is it called a cord, as you shall see anon in the speakynge of circles.
Matche cornersIn the meane season must I not omit to declare what angles bee called matche corners, that is to saie, suche as stande directly one against the other, when twoo lines be drawen a crosse, as here appereth.
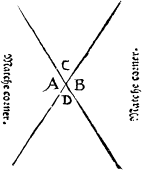
Where A. and B. are matche corners, so are C. and D. but not A. and C. nother D. and A.
Nowe will I beginne to speak of figures, that be properly so called, of whiche all be made of diuerse lines, except onely a circle, an egge forme, and a tunne forme, which .iij. haue no angle and haue but one line for their bounde, and an eye fourme whiche is made of one lyne, and hath an angle onely.
A circle.A circle is a figure made and enclosed with one line, and hath in the middell of it a pricke or centre, from whiche all the lines that be drawen to the circumference are equall all in length, as here you see.
Circumference.
And the line that encloseth the whole compasse, is called the circumference.
A diameter. And all the lines that bee drawen crosse the circle, and goe by the centre, are named diameters, whose halfe, I meane from the center to the circumference [B.i.v] any waie, Semidiameter. is called the semidiameter, or halfe diameter.
A cord, or a stringlyne.
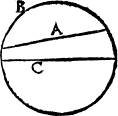
But and if the line goe crosse the circle, and passe beside the centre, then is it called a corde, or a stryng line, as I said before, and as this exaumple sheweth: where A. is the corde. And the compassed line that aunswereth to it, An archline is called an arche lyne, A bowline. or a bowe lyne, whiche here marked with B. and the diameter with C.
 |
 |
But and if that part be separate from the rest of the circle (as in this exãple you see) then ar both partes called cãtelles, A cantle the one the greatter cantle as E. and the other the lesser cantle, as D. And if it be parted iuste by the centre (as you see in F.) A semyecircle then is it called a semicircle, or halfe compasse.
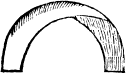
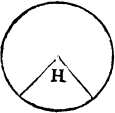
Sometimes it happeneth that a cantle is cutte out with two lynes drawen from the centre to the circumference (as G. is) A nooke cantle and then maie it be called a nooke cantle, and if it be not parted from the reste of the circle (as you see in H.) A nooke. then is it called a nooke plainely without any addicion. And the compassed lyne in it is called an arche lyne, as the exaumple here doeth shewe.
B ij
An arche.
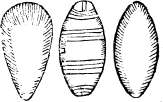
Nowe haue you heard as touchyng circles, meetely sufficient instruction, so that it should seme nedeles to speake any more of figures in that kynde, saue that there doeth yet remaine ij. formes of an imperfecte circle, for it is lyke a circle that were brused, and thereby did runne out endelong one waie, whiche forme Geometricians dooe call an An egge fourme. egge forme, because it doeth represent the figure and shape of an egge duely proportioned (as this figure sheweth) hauyng the one ende greate then the other.
A tunne or barrel form
A tunne forme.

An egge forme
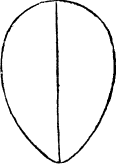
For if it be lyke the figure of a circle pressed in length, and bothe endes lyke bygge, then is it called a tunne forme, or barrell forme, the right makyng of whiche figures, I wyll declare hereafter in the thirde booke.
An other forme there is, whiche you maie call a nutte forme, and is made of one lyne muche lyke an egge forme, saue that it hath a sharpe angle.
And it chaunceth sometyme that there is a right line drawen crosse these figures, An axtre or axe lyne. and that is called an axelyne, or axtre. Howe be it properly that line that is called an axtre, whiche gooeth throughe the myddell of a Globe, for as a diameter is in a circle, so is an axe lyne or axtre in a Globe, [B.ii.v] that lyne that goeth from side to syde, and passeth by the middell of it. And the two poyntes that suche a lyne maketh in the vtter bounde or platte of the globe, are named polis, wch you may call aptly in englysh, tourne pointes: of whiche I do more largely intreate, in the booke that I haue written of the vse of the globe.

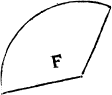
But to returne to the diuersityes of figures that remayne vndeclared, the most simple of them ar such ones as be made but of two lynes, as are the cantle of a circle, and the halfe circle, of which I haue spoken allready. Likewyse the halfe of an egge forme, the cantle of an egge forme, the halfe of a tunne fourme, and the cantle of a tunne fourme, and besyde these a figure moche like to a tunne fourne, saue that it is sharp couered at both the endes, and therfore doth consist of twoo lynes, where a tunne forme is made of one lyne, An yey fourme and that figure is named an yey fourme.
A triangle
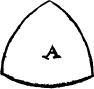
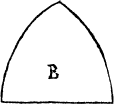
The nexte kynd of figures are those that be made of .iij. lynes other be all right lynes, all crooked lynes, other some right and some crooked. But what fourme so euer they be of, they are named generally triangles. for a triangle is nothinge els to say, but a figure of three corners. And thys is a generall rule, looke how many lynes any figure hath, so mannye corners it hath also, yf it bee a platte forme, and not a bodye. For a bodye hath dyuers lynes metyng sometime in one corner.
Now to geue you example of triangles, there is one whiche is all of croked lynes, and may be taken fur a portiõ of a globe as the figur marked wt A.
An other hath two compassed lines and one right lyne, and is as the portiõ of halfe a globe, example of B.
An other hath but one compassed B.iii lyne, and is the quarter of a circle, named a quadrate, and the ryght lynes make a right corner, as you se in C. Otherlesse then it as you se D, whose right lines make a sharpe corner, or greater then a quadrate, as is F, and then the right lynes of it do make a blunt corner.
 |
 |
 |
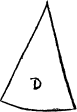
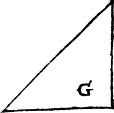
Also some triangles haue all righte lynes and they be distincted in sonder by their angles, or corners. for other their corners bee all sharpe, as you see in the figure, E. other ij. sharpe and one blunt, as is the figure G. other ij. sharp and one blunt as in the figure H.
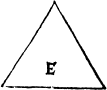
There is also an other distinction of the names of triangles, according to their sides, whiche other be all equal as in the figure E, and that the Greekes doo call Isopleuron, ἰσόπλευρομ. and Latine men æequilaterum: and in english it may be called a threlike triangle, other els two sydes bee equall and the thyrd vnequall, which the Greekes call Isosceles, ισόσκελεσ. the Latine men æquicurio, and in english tweyleke may they be called, as in G, H, and K. For, they may be of iij. kinds that is to say, with one square angle, as is G, or with a blunte corner as H, or with all in sharpe korners, as you see in K.
 |
 |
 |
Further more it may be yt they haue neuer a one syde equall to an other, and they be in iij kyndes also distinct lyke the twilekes, as you maye perceaue by these examples .M. N, and O. where M. hath a right angle, N, a blunte angle, and O, all sharpe angles σκαλενὄμ. these the Greekes and latine men do [B.iii.v] cal scalena and in englishe theye may be called nouelekes, for thei haue no side equall, or like lõg, to ani other in the same figur. Here it is to be noted, that in a triãgle al the angles bee called innerãgles except ani side bee drawenne forth in lengthe, for then is that fourthe corner caled an vtter corner, as in this exãple because A.B, is drawen in length, therfore the ãgle C, is called an vtter ãgle.
 |
 |
 |

Quadrãgle And thus haue I done with triãguled figures, and nowe foloweth quadrangles, which are figures of iiij. corners and of iiij. lines also, of whiche there be diuers kindes, but chiefely v. that is to say, A square quadrate. a square quadrate, whose sides bee all equall, and al the angles square, as you se here in this figure Q. A longe square. The second kind is called a long square, whose foure corners be all square, but the sides are not equall eche to other, yet is euery side equall to that other that is against it, as you maye perceaue in this figure .R.
[B.iiii.] A losenge

The thyrd kind is called losenges A diamõd. or diamondes, whose sides bee all equall, but it hath neuer a square corner, for two of them be sharpe, and the other two be blunt, as appeareth in .S.

The iiij. sorte are like vnto losenges, saue that they are longer one waye, and their sides be not equal, yet ther corners are like the corners of a losing, and therfore ar they named A losenge lyke. losengelike or diamõdlike, whose figur is noted with T. Here shal you marke that al those squares which haue their sides al equal, may be called also for easy vnderstandinge, likesides, as Q. and S. and those that haue only the contrary sydes equal, as R. and T. haue, those wyll I call likeiammys, for a difference.
The fift sorte doth containe all other fashions of foure cornered figurs, and ar called of the Grekes trapezia, of Latin mẽ mensulæ and of Arabitians, helmuariphe, they may be called in englishe borde formes, Borde formes. they haue no syde equall to an other as these examples shew, neither keepe they any rate in their corners, and therfore are they counted vnruled formes, and the other foure kindes onely are counted ruled formes, in the kynde of quadrangles. Of these vnruled formes ther is no numbre, they are so mannye and so dyuers, yet by arte they may be changed into other kindes of figures, and therby be brought to measure and proportion, as in the thirtene conclusion is partly taught, but more plainly in my booke of measuring you may see it.
[B.iiii.v]
And nowe to make an eande of the dyuers kyndes of figures, there dothe folowe now figures of .v. sydes, other .v. corners, which we may call cink-angles, whose sydes partlye are all equall as in A, and those are counted ruled cinkeangles, and partlye vnequall, as in B, and they are called vnruled.

Likewyse shall you iudge of siseangles, which haue sixe corners, septangles, whiche haue seuen angles, and so forth, for as mannye numbres as there maye be of sydes and angles, so manye diuers kindes be there of figures, vnto which yow shall geue names according to the numbre of their sides and angles, of whiche for this tyme I wyll make an ende, A squyre. and wyll sette forthe on example of a syseangle, whiche I had almost forgotten, and that is it, whose vse commeth often in Geometry, and is called a squire, is made of two long squares ioyned togither, as this example sheweth.
The globe as is before.
And thus I make an eand to speake of platte formes, and will briefelye saye somwhat touching the figures of bodeis which partly haue one platte forme for their bound, and yt iust roũd as a globe hath, or ended long as in an egge, and a tunne fourme, whose pictures are these.
Howe be it you must marke that I meane not the very figure of a tunne, when I saye tunne form, but a figure like a tunne, for a tune fourme, C hath but one plat forme, and therfore must needs be round at the endes, where as a tunne hath thre platte formes, and is flatte at eche end, as partly these pictures do shewe.
Bodies of two plattes, are other cantles or halues of those other bodies, that haue but one platte forme, or els they are lyke in foorme to two such cantles ioyned togither as this A. doth partly expresse: A rounde spier. or els it is called a rounde spire, or stiple fourme, as in this figure is some what expressed.
![]()
![]()
Nowe of three plattes there are made certain figures of bodyes, as the cantels and halues of all bodyes that haue but ij. plattys, and also the halues of halfe globys and canteles of a globe. Lykewyse a rounde piller, and a spyre made of a rounde spyre, slytte in ij. partes long ways.
But as these formes be harde to be iudged by their pycturs, so I doe entende to passe them ouer with a great number of other formes of bodyes, which afterwarde shall be set forth in the boke of Perspectiue, bicause that without perspectiue knowledge, it is not easy to iudge truly the formes of them in flatte protacture.
And thus I made an ende for this tyme, of the defi-
nitions Geometricall, appertayning to this
parte of practise, and the rest wil
I prosecute as cause shall
serue.
THE PRACTIKE WORKINGE
OF
sondry conclusions geometrical.
THE FYRST CONCLVSION.
To make a threlike triangle on any lyne measurable.
 ake the iuste lẽgth of the lyne with your cõpasse, and stay the one foot
of the compas in one of the endes of that line, turning the other vp or
doun at your will, drawyng the arche of a circle against the midle of
the line, and doo like wise with the same cõpasse vnaltered, at the
other end of the line, and wher these ij. croked lynes doth crosse,
frome thence drawe a lyne to ech end of your first line, and there shall
appear a threlike triangle drawen on that line.
ake the iuste lẽgth of the lyne with your cõpasse, and stay the one foot
of the compas in one of the endes of that line, turning the other vp or
doun at your will, drawyng the arche of a circle against the midle of
the line, and doo like wise with the same cõpasse vnaltered, at the
other end of the line, and wher these ij. croked lynes doth crosse,
frome thence drawe a lyne to ech end of your first line, and there shall
appear a threlike triangle drawen on that line.
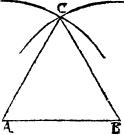
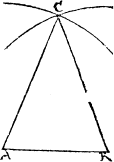
Example.
A.B. is the first line, on which I wold make the threlike triangle, therfore I open the compasse as wyde as that line is long, and draw two arch lines that mete in C, then from C, I draw ij other lines one to A, another to B, and than I haue my purpose.
 |
 |
 |
THE .II. CONCLVSION
If you wil make a twileke or a nouelike triangle on ani certaine
line.
Consider fyrst the length that yow will haue the other sides to containe, and to that length open your compasse, and C.ij. then worke as you did in the threleke triangle, remembryng this, that in a nouelike triangle you must take ij. lengthes besyde the fyrste lyne, and draw an arche lyne with one of thẽ at the one ende, and with the other at the other end, the exãple is as in the other before.
THE III. CONCL.
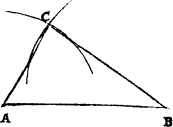
To diuide an angle of right lines into ij. equal partes.
First open your compasse as largely as you can, so that it do not excede the length of the shortest line yt incloseth the angle. Then set one foote of the compasse in the verye point of the angle, and with the other fote draw a compassed arch frõ the one lyne of the angle to the other, that arch shall you deuide in halfe, and thẽ draw a line frõ the ãgle to ye middle of ye arch, and so ye angle is diuided into ij. equall partes.
Example.
Let the triãgle be A.B.C, thẽ set I one foot of ye cõpasse in B, and with the other I draw ye arch D.E, which I part into ij. equall parts in F, and thẽ draw a line frõ B, to F, & so I haue mine intẽt.
THE IIII. CONCL.
To deuide any measurable line into ij. equall partes.
Open your compasse to the iust lẽgth of ye line. And thẽ set one foote steddely at the one ende of the line, & wt the other fote draw an arch of a circle against ye midle of the line, both ouer it, and also vnder it, then doo lykewaise [C.ii.v] at the other ende of the line. And marke where those arche lines do meet crosse waies, and betwene those ij. pricks draw a line, and it shall cut the first line in two equall portions.
Example.
The lyne is A.B. accordyng to which I open the compasse and make .iiij. arche lines, whiche meete in C. and D, then drawe I a lyne from C, so haue I my purpose.
This conlusion serueth for makyng of quadrates and squires, beside many other commodities, howebeit it maye bee don more readylye by this conclusion that foloweth nexte.
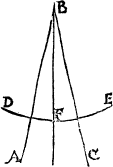
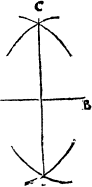
THE FIFT CONCLVSION.
To make a plumme line or any pricke that you will in any right lyne
appointed.
Open youre compas so that it be not wyder then from the pricke appoynted in the line to the shortest ende of the line, but rather shorter. Then sette the one foote of the compasse in the first pricke appointed, and with the other fote marke ij. other prickes, one of eche syde of that fyrste, afterwarde open your compasse to the wydenes of those ij. new prickes, and draw from them ij. arch lynes, as you did in the fyrst conclusion, for making of a threlyke triãgle. then if you do mark their crossing, and from it drawe a line to your fyrste pricke, it shall bee a iust plum lyne on that place.
Example.
The lyne is A.B. the prick on whiche I shoulde make the plumme lyne, is C. then open I the compasse as wyde as A.C, and sette one foot in C. and with the other doo I marke out C.A. and C.B, then open I the compasse as wide as A.B, and make ij. arch lines which do crosse in D, and so haue I doone.
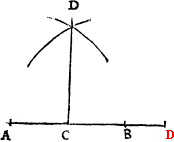
Howe bee it, it happeneth so sommetymes, that the C iij pricke on whiche you would make the perpendicular or plum line, is so nere the eand of your line, that you can not extende any notable length from it to thone end of the line, and if so be it then that you maie not drawe your line lenger frõ that end, then doth this conclusion require a newe ayde, for the last deuise will not serue. In suche case therfore shall you dooe thus: If your line be of any notable length, deuide it into fiue partes. And if it be not so long that it maie yelde fiue notable partes, then make an other line at will, and parte it into fiue equall portiõs: so that thre of those partes maie be found in your line. Then open your compas as wide as thre of these fiue measures be, and sette the one foote of the compas in the pricke, where you would haue the plumme line to lighte (whiche I call the first pricke,) and with the other foote drawe an arche line righte ouer the pricke, as you can ayme it: then open youre compas as wide as all fiue measures be, and set the one foote in the fourth pricke, and with the other foote draw an other arch line crosse the first, and where thei two do crosse, thense draw a line to the poinct where you woulde haue the perpendicular line to light, and you haue doone.
Example.
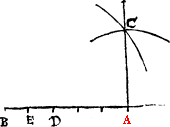
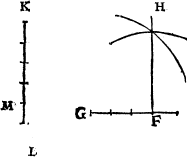
The line is A.B. and A. is the prick, on whiche the perpendicular line must light. Therfore I deuide A.B. into fiue partes equall, then do I open the compas to the widenesse of three partes (that is A.D.) and let one foote staie in A. and with the other I make an arche line in C. Afterwarde I open the compas as wide as A.B. [C.iii.v] (that is as wide as all fiue partes) and set one foote in the .iiij. pricke, which is E, drawyng an arch line with the other foote in C. also. Then do I draw thence a line vnto A, and so haue I doone. But and if the line be to shorte to be parted into fiue partes, I shall deuide it into iij. partes only, as you see the liue F.G, and then make D. an other line (as is K.L.) whiche I deuide into .v. suche diuisions, as F.G. containeth .iij, then open I the compass as wide as .iiij. partes (whiche is K.M.) and so set I one foote of the compas in F, and with the other I drawe an arch lyne toward H, then open I the cõpas as wide as K.L. (that is all .v. partes) and set one foote in G, (that is the iij. pricke) and with the other I draw an arch line toward H. also: and where those .ij. arch lines do crosse (whiche is by H.) thence draw I a line vnto F, and that maketh a very plumbe line to F.G, as my desire was. The maner of workyng of this conclusion, is like to the second conlusion, but the reason of it doth depẽd of the .xlvi. proposiciõ of ye first boke of Euclide. An other waie yet. set one foote of the compas in the prick, on whiche you would haue the plumbe line to light, and stretche forth thother foote toward the longest end of the line, as wide as you can for the length of the line, and so draw a quarter of a compas or more, then without stirryng of the compas, set one foote of it in the same line, where as the circular line did begin, and extend thother in the circular line, settyng a marke where it doth light, then take half that quantitie more there vnto, and by that prick that endeth the last part, draw a line to the pricke assigned, and it shall be a perpendicular.
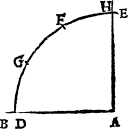
Example.
A.B. is the line appointed, to whiche I must make a perpendicular line to light in the pricke assigned, which is A. Therfore doo I set one foote of the compas in A, and extend the other vnto D. makyng a part of a circle, [C.iiii.] more then a quarter, that is D.E. Then do I set one foote of the compas vnaltered in D, and stretch the other in the circular line, and it doth light in F, this space betwene D. and F. I deuide into halfe in the pricke G, whiche halfe I take with the compas, and set it beyond F. vnto H, and thefore is H. the point, by whiche the perpendicular line must be drawn, so say I that the line H.A, is a plumbe line to A.B, as the conclusion would.
THE .VI. CONCLVSION.
To drawe a streight line from any pricke that is not in a line, and to
make it perpendicular to an other line.
Open your compas as so wide that it may extend somewhat farther, thẽ from the prick to the line, then sette the one foote of the compas in the pricke, and with the other shall you draw a cõpassed line, that shall crosse that other first line in .ij. places. Now if you deuide that arch line into .ij. equall partes, and from the middell pricke therof vnto the prick without the line you drawe a streight line, it shalbe a plumbe line to that firste lyne, accordyng to the conclusion.
Example.
C. is the appointed pricke, from whiche vnto the line A.B. I must draw a perpẽdicular. Thefore I open the cõpas so wide, that it may haue one foote in C, and thother to reach ouer the line, and with yt foote I draw an arch line as you see, betwene A. and B, which arch line I deuide in the middell in the point D. Then drawe I a line from C. to D, and it is perpendicular to the line A.B, accordyng as my desire was.
[C.iiii.v]
THE .VII. CONCLVSION.
To make a plumbe lyne on any porcion of a circle, and that on the vtter or inner
bughte.
Mark first the prick where ye plũbe line shal lyght: and prick out of ech side of it .ij. other poinctes equally distant from that first pricke. Then set the one foote of the cõpas in one of those side prickes, and the other foote in the other side pricke, and first moue one of the feete and drawe an arche line ouer the middell pricke, then set the compas steddie with the one foote in the other side pricke, and with the other foote drawe an other arche line, that shall cut that first arche, and from the very poincte of their meetyng, drawe a right line vnto the firste pricke, where you do minde that the plumbe line shall lyghte. And so haue you performed thintent of this conclusion.
Example.
The arche of the circle on whiche I would erect a plumbe line, is A.B.C. and B. is the pricke where I would haue the plumbe line to light. Therfore I meate out two equall distaunces on eche side of that pricke B. and they are A.C. Then open I the compas as wide as A.C. and settyng one of the feete in A. with the other I drawe an arche line which goeth by G. Like waies I set one foote of the compas steddily in C. and with the other I drawe an arche line, goyng by G. also. Now consideryng that G. is the pricke of their meetyng, it shall be also the poinct fro whiche I must drawe the plũbe line. Then draw I a right line from G. to B. and so haue mine intent. Now as A.B.C. hath a plumbe line erected on his D vtter bought, so may I erect a plumbe line on the inner bught of D.E.F, doynge with it as I did with the other, that is to saye, fyrste settyng forthe the pricke where the plumbe line shall light, which is E, and then markyng one other on eche syde, as are D. and F. And then proceding as I dyd in the example before.
THE VIII. CONCLVSYON.
How to deuide the arche of a circle into two equall partes, without
measuring the arche.
Deuide the corde of that line info ij. equall portions, and then from the middle prycke erecte a plumbe line, and it shal parte that arche in the middle.
Example.
The arch to be diuided ys A.D.C, the corde is A.B.C, this corde is diuided in the middle with B, from which prick if I erect a plum line as B.D, thẽ will it diuide the arch in the middle, that is to say, in D.
THE IX. CONCLVSION.
To do the same thynge other wise. And for shortenes of worke, if you wyl make a plumbe line without much labour, you may do it with your squyre, so that it be iustly made, for yf you applye the edge of the squyre to the line in which the prick is, and foresee the very corner of the squyre doo touche the pricke. And than frome that corner if you drawe a lyne by the other edge of the squyre, yt will be perpendicular to the former line.
[D.i.v]
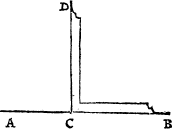
Example.
A.B. is the line, on which I wold make the plumme line, or perpendicular. And therefore I marke the prick, from which the plumbe lyne muste rise, which here is C. Then do I sette one edg of my squyre (that is B.C.) to the line A.B, so at the corner of the squyre do touche C. iustly. And from C. I drawe a line by the other edge of the squire, (which is C.D.) And so haue I made the plumme line D.C, which I sought for.
THE X. CONCLVSION.
How to do the same thinge an other way yet
If so be it that you haue an arche of suche greatnes, that your squyre wyll not suffice therto, as the arche of a brydge or of a house or window, then may you do this. Mete vnderneth the arch where ye midle of his cord wyl be, and ther set a mark. Then take a long line with a plummet, and holde the line in suche a place of the arch, that the plummet do hang iustely ouer the middle of the corde, that you didde diuide before, and then the line doth shewe you the middle of the arche.
Example.
The arch is A.D.B, of which I trye the midle thus. I draw a corde from one syde to the other (as here is A.B,) which I diuide in the middle in C. Thẽ take I a line with a plummet (that is D.E,) and so hold I the line that the plummet E, dooth hange ouer C, And D ij. then I say that D. is the middle of the arche. And to thentent that my plummet shall point the more iustely, I doo make it sharpe at the nether ende, and so may I trust this woorke for certaine.
THE XI. CONCLVSION.
When any line is appointed and without it a pricke, whereby a parallel
must be drawen howe you shall doo it.
Take the iuste measure beetwene the line and the pricke, accordinge to which you shal open your compasse. Thẽ pitch one foote of your compasse at the one ende of the line, and with the other foote draw a bowe line right ouer the pytche of the compasse, lyke-wise doo at the other ende of the lyne, then draw a line that shall touche the vttermoste edge of bothe those bowe lines, and it will bee a true parallele to the fyrste lyne appointed.
Example.
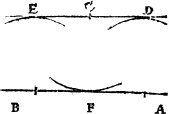
A.B, is the line vnto which I must draw an other gemow line, which muste passe by the prick C, first I meate with my compasse the smallest distance that is from C. to the line, and that is C.F, wherfore staying the compasse at that distaunce, I seete the one foote in A, and with the other foot I make a bowe lyne, which is D, thẽ like wise set I the one foote of the compasse in B, and with the other I make the second bow line, which is E. And then draw I a line, so that it toucheth the vttermost edge of bothe these bowe lines, and that lyne passeth by the pricke C, end is a gemowe line to A.B, as my sekyng was.
[D.ii.v]THE .XII. CONCLVSION.
To make a triangle of any .iij. lines, so that the lines be suche, that any .ij. of them be longer then the thirde. For this rule is generall, that any two sides of euerie triangle taken together, are longer then the other side that remaineth.
If you do remember the first and seconde conclusions, then is there no difficultie in this, for it is in maner the same woorke. First cõsider the .iij. lines that you must take, and set one of thẽ for the ground line, then worke with the other .ij. lines as you did in the first and second conclusions.
Example.
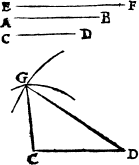
I haue .iij. A.B. and C.D. and E.F. of whiche I put .C.D. for my ground line, then with my compas I take the length of .A.B. and set the one foote of my compas in C, and draw an arch line with the other foote. Likewaies I take the lẽgth of E.F, and set one foote in D, and with the other foote I make an arch line crosse the other arche, and the pricke of their metyng (whiche is G.) shall be the thirde corner of the triangle, for in all suche kyndes of woorkynge to make a tryangle, if you haue one line drawen, there remayneth nothyng els but to fynde where the pitche of the thirde corner shall bee, for two of them must needes be at the two eandes of the lyne that is drawen.
D.iij.THE XIII. CONCLVSION.
If you haue a line appointed, and a pointe in it limited, howe you maye make on it a righte lined angle, equall to an other right lined angle, all ready assigned.
Fyrste draw a line against the corner assigned, and so is it a triangle, then take heede to the line and the pointe in it assigned, and consider if that line from the pricke to this end bee as long as any of the sides that make the triangle assigned, and if it bee longe enoughe, then prick out there the length of one of the lines, and then woorke with the other two lines, accordinge to the laste conlusion, makynge a triangle of thre like lynes to that assigned triangle. If it bee not longe inoughe, thenn lengthen it fyrste, and afterwarde doo as I haue sayde beefore.
Example.
Lette the angle appoynted bee A.B.C, and the corner assigned, B. Farthermore let the lymited line bee D.G, and the pricke assigned D.
Fyrste therefore by drawinge the line A.C, I make the triangle A.B.C.
Then consideringe that D.G, is longer thanne A.B, you shall cut out a line frõ D. toward G, equal to A.B, as for exãple D.F. Thẽ measure oute the other ij. lines and worke with thẽ according as the conclusion with the fyrste also and the second teacheth yow, and then haue you done.
[D.iii.v]
THE XIIII. CONCLVSION.
To make a square quadrate of any righte lyne appoincted.
First make a plumbe line vnto your line appointed, whiche shall light at one of the endes of it, accordyng to the fifth conclusion, and let it be of like length as your first line is, then opẽ your compasse to the iuste length of one of them, and sette one foote of the compasse in the ende of the one line, and with the other foote draw an arche line, there as you thinke that the fowerth corner shall be, after that set the one foote of the same compasse vnsturred, in the eande of the other line, and drawe an other arche line crosse the first archeline, and the poincte that they do crosse in, is the pricke of the fourth corner of the square quadrate which you seke for, therfore draw a line from that pricke to the eande of eche line, and you shall therby haue made a square quadrate.
Example.
A.B. is the line proposed, of whiche I shall make a square quadrate, therefore firste I make a plũbe line vnto it, whiche shall lighte in A, and that plũb line is A.C, then open I my compasse as wide as the length of A.B, or A.C, (for they must be bothe equall) and I set the one foote of thend in C, and with the other I make an arche line nigh vnto D, afterward I set the compas again with one foote in B, and with the other foote I make an arche line crosse the first arche line in D, and from the prick of their crossyng I draw .ij. lines, one to B, and an other to C, and so haue I made the square quadrate that I entended.
[D.iiii.]
THE .XV. CONCLVSION.
To make a likeiãme equall to a triangle appointed, and that in a right
lined ãgle limited.
First from one of the angles of the triangle, you shall drawe a gemowe line, whiche shall be a parallele to that syde of the triangle, on whiche you will make that likeiamme. Then on one end of the side of the triangle, whiche lieth against the gemowe lyne, you shall draw forth a line vnto the gemow line, so that one angle that commeth of those .ij. lines be like to the angle which is limited vnto you. Then shall you deuide into ij. equall partes that side of the triangle whiche beareth that line, and from the pricke of that deuision, you shall raise an other line parallele to that former line, and continewe it vnto the first gemowe line, and thẽ of those .ij. last gemowe lynes, and the first gemowe line, with the halfe side of the triangle, is made a lykeiamme equall to the triangle appointed, and hath an angle lyke to an angle limited, accordyng to the conclusion.
Example.
B.C.G, is the triangle appoincted vnto, whiche I muste make an equall likeiamme. And D, is the angle that the likeiamme must haue. Therfore first entendyng to erecte the likeiãme on the one side, that the ground line of the triangle (whiche is B.G.) I do draw a gemow line by C, and make it parallele to the ground line B.G, and that new gemow line is A.H. Then do I raise a line from B. vnto the gemowe line, (whiche line is A.B) and make an angle equall to D, that is the appointed angle (accordyng as the .viij. cõclusion teacheth) and that angle is B.A.E. Then to procede, I doo parte in ye middle the said groũd line B.G, in the prick F, frõ which prick I draw [D.iiii.v] to the first gemowe line (A.H.) an other line that is parallele to A.B, and that line is E.F. Now saie I that the likeiãme B.A.E.F, is equall to the triangle B.C.G. And also that it hath one angle (that is B.A.E.) like to D. the angle that was limitted. And so haue I mine intent. The profe of the equalnes of those two figures doeth depend of the .xli. proposition of Euclides first boke, and is the .xxxi. proposition of this second boke of Theoremis, whiche saieth, that whan a tryangle and a likeiamme be made betwene .ij. selfe same gemow lines, and haue their ground line of one length, then is the likeiamme double to the triangle, wherof it foloweth, that if .ij. suche figures so drawen differ in their ground line onely, so that the ground line of the likeiamme be but halfe the ground line of the triangle, then be those .ij. figures equall, as you shall more at large perceiue by the boke of Theoremis, in ye .xxxi. theoreme.
THE .XVI. CONCLVSION.
To make a likeiamme equall to a triangle appoincted, accordyng to an
angle limitted, and on a line also assigned.
In the last conclusion the sides of your likeiamme wer left to your libertie, though you had an angle appoincted. Nowe in this conclusion you are somwhat more restrained of libertie sith the line is limitted, which must be the side of the likeiãme. Therfore thus shall you procede. Firste accordyng to the laste conclusion, make a likeiamme in the angle appoincted, equall to the triangle that is assigned. Then with your compasse take the length of your line appointed, and set out two lines of the same length in the second gemowe lines, beginnyng at the one side of the likeiamme, and by those two prickes shall you draw an other gemowe line, whiche shall be parallele to two sides of the likeiamme. Afterward shall you draw .ij. lines more for the accomplishement of your worke, which better shall be E. perceaued by a shorte exaumple, then by a greate numbre of wordes, only without example, therefore I wyl by example sette forth the whole worke.
Example.
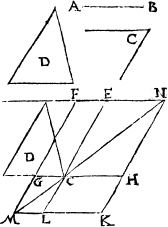
Fyrst, according to the last conclusion, I make the likeiamme E.F.C.G, equal to the triangle D, in the appoynted angle whiche is E. Then take I the lengthe of the assigned line (which is A.B,) and with my compas I sette forthe the same lẽgth in the ij. gemow lines N.F. and H.G, setting one foot in E, and the other in N, and againe settyng one foote in C, and the other in H. Afterward I draw a line from N. to H, whiche is a gemow lyne, to ij. sydes of the likeiamme. thenne drawe I a line also from N. vnto C. and extend it vntyll it crosse the lines, E.L. and F.G, which both must be drawen forth longer then the sides of the likeiamme. and where that lyne doeth crosse F.G, there I sette M. Nowe to make an ende, I make an other gemowe line, whiche is parallel to N.F. and H.G, and that gemowe line doth passe by the pricke M, and then haue I done. Now say I that H.C.K.L, is a likeiamme equall to the triangle appointed, whiche was D, and is made of a line assigned that is A.B, for H.C, is equall vnto A.B, and so is K.L. The profe of ye equalnes of this likeiam vnto the triãgle, depẽdeth of the thirty and two Theoreme: as in the boke of Theoremes doth appear, where it is declared, that in al likeiammes, whẽ there are more then one made about one bias line, the filsquares of euery of them muste needes be equall.
[E.i.v]
THE XVII. CONCLVSION.
To make a likeiamme equal to any right lined figure, and that on an
angle appointed.
The readiest waye to worke this conclusion, is to tourn that rightlined figure into triangles, and then for euery triangle together an equal likeiamme, according vnto the eleuen cõclusion, and then to ioine al those likeiammes into one, if their sides happen to be equal, which thing is euer certain, when al the triangles happẽ iustly betwene one pair of gemow lines. but and if they will not frame so, then after that you haue for the firste triangle made his likeiamme, you shall take the lẽgth of one of his sides, and set that as a line assigned, on whiche you shal make the other likeiams, according to the twelft cõclusion, and so shall you haue al your likeiammes with ij. sides equal, and ij. like angles, so yt you mai easily ioyne thẽ into one figure.
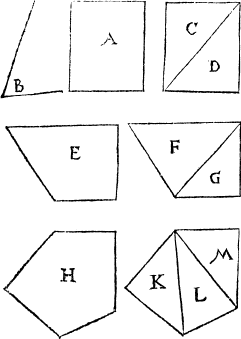
Example.
If the right lined figure be like vnto A, thẽ may it be turned into triangles that wil stãd betwene ij. parallels anye ways, as you mai se by C. and D, for ij. sides of both the triãngles ar parallels. Also if the right lined figure be like vnto E, thẽ wil it be turned into triãgles, liyng betwene two parallels also, as ye other did before, as in the exãple of F.G. But and if ye E .ij. right lined figure be like vnto H, and so turned into triãgles as you se in K.L.M, wher it is parted into iij triãgles, thẽ wil not all those triangles lye betwen one pair of parallels or gemow lines, but must haue many, for euery triangle must haue one paire of parallels seuerall, yet it maye happen that when there bee three or fower triangles, ij. of theym maye happen to agre to one pair of parallels, whiche thinge I remit to euery honest witte to serche, for the manner of their draught wil declare, how many paires of parallels they shall neede, of which varietee bicause the examples ar infinite, I haue set forth these few, that by them you may coniecture duly of all other like.
Further explicacion you shal not greatly neede, if you remembre what hath ben taught before, and then diligẽtly behold how these sundry figures be turned into triãgles. In the fyrst you se I haue made v. triangles, and four paralleles. in the seconde vij. triangles and foure paralleles. in the thirde thre triãgles, and fiue parallels, in the iiij. you se fiue triãgles & four parallels. in the fift, iiij. triãgles and .iiij. parallels, & in ye sixt ther ar fiue triãgles & iiij. paralels. Howbeit a mã maye at liberty alter them into diuers formes of triãgles & therefore I [E.ii.v] leue it to the discretion of the woorkmaister, to do in al suche cases as he shal thinke best, for by these examples (if they bee well marked) may all other like conclusions be wrought.
THE XVIII. CONCLVSION.
To parte a line assigned after suche a sorte, that the square that is made of the whole line and one of his parts, shal be equal to the squar that cometh of the other parte alone.
First deuide your lyne into ij. equal parts, and of the length of one part make a perpendicular to light at one end of your line assigned. then adde a bias line, and make thereof a triangle, this done if you take from this bias line the halfe lengthe of your line appointed, which is the iuste length of your perpendicular, that part of the bias line whiche dothe remayne, is the greater portion of the deuision that you seke for, therefore if you cut your line according to the lengthe of it, then will the square of that greater portion be equall to the square that is made of the whole line and his lesser portion. And contrary wise, the square of the whole line and his lesser parte, wyll be equall to the square of the greater parte.
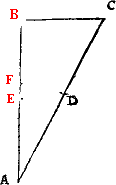
Example.
A.B, is the lyne assigned. E. is the middle pricke of A.B, B.C. is the plumb line or perpendicular, made of the halfe of A.B, equall to A.E, other B.E, the byas line is C.A, from whiche I cut a peece, that is C.D, equall to C.B, and accordyng to the lengthe lo the peece that remaineth (whiche is D.A,) I doo deuide the line A.B, at whiche diuision I set F. Now say I, that this line A.B, (wch was assigned vnto me) is so diuided in this point F, yt ye square of ye hole line A.B, & of the one portiõ (yt is F.B, the E iij lesser part) is equall to the square of the other parte, whiche is F.A, and is the greater part of the first line. The profe of this equalitie shall you learne by the .xl. Theoreme.
There are two ways to make this Example work:
—transpose E and F in the illustration, and change one occurrence
of E to F in the text, or:
—keep the illustration as printed, and transpose all other
occurrences of E and F in the text.
THE .XIX. CONCLVSION.
To make a square quadrate equall to any right lined figure
appoincted.
First make a likeiamme equall to that right lined figure, with a right angle, accordyng to the .xi. conclusion, then consider the likeiamme, whether it haue all his sides equall, or not: for yf they be all equall, then haue you doone your conclusion. but and if the sides be not all equall, then shall you make one right line iuste as long as two of those vnequall sides, that line shall you deuide in the middle, and on that pricke drawe half a circle, then cutte from that diameter of the halfe circle a certayne portion equall to the one side of the likeiamme, and from that pointe of diuision shall you erecte a perpendicular, which shall touche the edge of the circle. And that perpendicular shall be the iuste side of the square quadrate, equall both to the lykeiamme, and also to the right lined figure appointed, as the conclusion willed.
Example.
K, is the right lined figure appointed, and B.C.D.E, is the likeiãme, with right angles equall vnto K, but because that this likeiamme is not a square quadrate, I must turne it into such one after this sort, I shall make one right line, as long as .ij. vnequall sides of the likeiãme, that line here is F.G, whiche is equall to B.C, and C.E. Then part I that line in the middle in the [E.iii.v] pricke M, and on that pricke I make halfe a circle, accordyng to the length of the diameter F.G. Afterward I cut awaie a peece from F.G, equall to C.E, markyng that point with H. And on that pricke I erecte a perpendicular H.K, whiche is the iust side to the square quadrate that I seke for, therfore accordyng to the doctrine of the .x. conclusion, of the lyne I doe make a square quadrate, and so haue I attained the practise of this conclusion.
THE .XX. CONCLVSION.
When any .ij. square quadrates are set forth, how you maie make one
equall to them bothe.
First drawe a right line equall to the side of one of the quadrates: and on the ende of it make a perpendicular, equall in length to the side of the other quadrate, then drawe a byas line betwene those .ij. other lines, makyng thereof a right angeled triangle. And that byas lyne wyll make a square quadrate, equall to the other .ij. quadrates appointed.
Example.
A.B. and C.D, are the two square quadrates appointed, vnto which I must make one equall square quadrate. First therfore I dooe make a righte line E.F, equall to one of the sides of the square quadrate A.B. And on the one end of it I make a plumbe line E.G, equall to the side of the other quadrate D.C. Then drawe I a byas line G.F, which beyng made the side of a quadrate [E.iiii.] (accordyng to the tenth conclusion) will accomplishe the worke of this practise: for the quadrate H. is muche iust as the other two. I meane A.B. and D.C.
THE .XXI. CONCLVSION.
When any two quadrates be set forth, howe to make a squire about the one
quadrate, whiche shall be equall to the other quadrate.
Determine with your selfe about whiche quadrate you wil make the squire, and drawe one side of that quadrate forth in lengte, accordyng to the measure of the side of the other quadrate, whiche line you maie call the grounde line, and then haue you a right angle made on this line by an other side of the same quadrate: Therfore turne that into a right cornered triangle, accordyng to the worke in the laste conclusion, by makyng of a byas line, and that byas lyne will performe the worke of your desire. For if you take the length of that byas line with your compasse, and then set one foote of the compas in the farthest angle of the first quadrate (whiche is the one ende of the groundline) and extend the other foote on the same line, accordyng to the measure of the byas line, and of that line make a quadrate, enclosyng ye first quadrate, then will there appere the forme of a squire about the first quadrate, which squire is equall to the second quadrate.
Example.
The first square quadrate is A.B.C.D, and the seconde is E. Now would I make a squire about the quadrate A.B.C.D, whiche shall bee equall vnto the quadrate E.
[E.iiii.v]Therfore first I draw the line A.D, more in length, accordyng to the measure of the side of E, as you see, from D. vnto F, and so the hole line of bothe these seuerall sides is A.F, thẽ make I a byas line from C, to F, whiche byas line is the measure of this woorke. wherefore I open my compas accordyng to the length of that byas line C.F, and set the one compas foote in A, and extend thother foote of the compas toward F, makyng this pricke G, from whiche I erect a plumbeline G.H, and so make out the square quadrate A.G.H.K, whose sides are equall eche of them to A.G. And this square doth contain the first quadrate A.B.C.D, and also a squire G.H.K, whiche is equall to the second quadrate E, for as the last conclusion declareth, the quadrate A.G.H.K, is equall to bothe the other quadrates proposed, that is A.B.C.D, and E. Then muste the squire G.H.K, needes be equall to E, consideryng that all the rest of that great quadrate is nothyng els but the quadrate self, A.B.C.D, and so haue I thintent of this conclusion.
THE .XXII. CONCLVSION.
To find out the cẽtre of any circle assigned.
Draw a corde or stryngline crosse the circle, then deuide into .ij. equall partes, both that corde, and also the bowe line, or arche line, that serueth to that corde, and from the prickes of those diuisions, if you drawe an other line crosse the circle, it must nedes passe by the centre. Therfore deuide that line in the middle, and that middle pricke is the centre of the circle proposed.
Example.
Let the circle be A.B.C.D, whose centre I shall seke. First therfore I draw a corde crosse the circle, that is A.C. Then do I deuide that corde in the middle, in E, and likewaies also do I deuide his arche line A.B.C, in the middle, in the pointe B. Afterward I drawe a line from B. to E, and so crosse the F. circle, whiche line is B.D, in which line is the centre that I seeke for. Therefore if I parte that line B.D, in the middle in to two equall portions, that middle pricke (which here is F) is the verye centre of the sayde circle that I seke. This conclusion may other waies be wrought, as the moste part of conclusions haue sondry formes of practise, and that is, by makinge thre prickes in the circũference of the circle, at liberty where you wyll, and then findinge the centre to those thre pricks, Which worke bicause it serueth for sondry vses, I think meet to make it a seuerall conclusion by it selfe.
THE XXIII. CONCLVSION.
To find the commen centre belongyng to anye three prickes appointed, if
they be not in an exacte right line.
It is to be noted, that though euery small arche of a greate circle do seeme to be a right lyne, yet in very dede it is not so, for euery part of the circumference of al circles is compassed, though in litle arches of great circles the eye cannot discerne the crokednes, yet reason doeth alwais declare it, therfore iij. prickes in an exact right line can not bee brought into the circumference of a circle. But and if they be not in a right line how so euer they stande, thus shall you find their cõmon centre. Opẽ your compas so wide, that it be somewhat more then the [F.i.v] halfe distance of two of those prickes. Then sette the one foote of the compas in the one pricke, and with the other foot draw an arche lyne toward the other pricke, Then againe putte the foot of your compas in the second pricke, and with the other foot make an arche line, that may crosse the firste arch line in ij. places. Now as you haue done with those two pricks, so do with the middle pricke, and the thirde that remayneth. Then draw ij. lines by the poyntes where those arche lines do crosse, and where those two lines do meete, there is the centre that you seeke for.
Example
The iij. prickes I haue set to be A.B, and C, whiche I wold bring into the edg of one common circle, by finding a centre cõmen to them all, fyrst therefore I open my cõpas, so that thei occupye more then ye halfe distance betwene ij. pricks (as are A.B.) and so settinge one foote in A. and extendinge the other toward B, I make the arche line D.E. Likewise settĩg one foot in B, and turninge the other toward A, I draw an other arche line that crosseth the first in D. and E. Then from D. to E, I draw a right lyne D.H. After this I open my cõpasse to a new distance, and make ij. arche lines betwene B. and C, whiche crosse one the other in F. and G, by whiche two pointes I draw an other line, that is F.H. And bycause that the lyne D.H. and the lyne F.H. doo meete in H, I saye that H. is the centre that serueth to those iij. prickes. Now therfore if you set one foot of your compas in H, and extend the other to any of the iij. pricks, you may draw a circle wch shal enclose those iij. pricks in the edg of his circũferẽce & thus haue you attained ye vse of this cõclusiõ.
F .ij
THE XXIIII. CONCLVSION.
To drawe a touche line onto a circle, from any poincte
assigned.
Here must you vnderstand that the pricke must be without the circle, els the conclusion is not possible. But the pricke or poinct beyng without the circle, thus shall you procede: Open your compas, so that the one foote of it maie be set in the centre of the circle, and the other foote on the pricke appoincted, and so draw an other circle of that largenesse about the same centre: and it shall gouerne you certainly in makyng the said touche line. For if you draw a line frõ the pricke appointed vnto the centre of the circle, and marke the place where it doeth crosse the lesser circle, and from that poincte erect a plumbe line that shall touche the edge of the vtter circle, and marke also the place where that plumbe line crosseth that vtter circle, and from that place drawe an other line to the centre, takyng heede where it crosseth the lesser circle, if you drawe a plumbe line from that pricke vnto the edge of the greatter circle, that line I say is a touche line, drawen from the point assigned, according to the meaning of this conclusion.
Example.
Let the circle be called B.C.D, and his cẽtre E, and ye prick assigned A, opẽ your cõpas now of such widenes, yt the one foote may be set in E, wch is ye cẽtre of ye circle, & ye other in A, wch is ye pointe assigned, & so make an other greter circle (as here is A.F.G) thẽ draw a line from A. vnto E, and wher that line doth cross ye inner circle (wch heere is in the prick B.) there erect a plũb line vnto the line. A.E. and let that plumb line touch the vtter circle, as it doth here in the point F, so shall B.F. bee that plumbe lyne. Then from F. vnto E. [F.ii.v] drawe an other line whiche shal be F.E, and it will cutte the inner circle, as it doth here in the point C, from which pointe C. if you erect a plumb line vnto A, then is that line A.C, the touche line, whiche you shoulde finde. Not withstandinge that this is a certaine waye to fynde any touche line, and a demonstrable forme, yet more easyly by many folde may you fynde and make any suche line with a true ruler, layinge the edge of the ruler to the edge of the circle and to the pricke, and so drawing a right line, as this example sheweth, where the circle is E, the pricke assigned is A. and the ruler C.D. by which the touch line is drawen, and that is A.B, and as this way is light to doo, so is it certaine inoughe for any kinde of workinge.
THE XXV. CONCLVSION.
When you haue any peece of the circumference of a circle assigned, howe
you may make oute the whole circle agreynge therevnto.
First seeke out of the centre of that arche, according to the doctrine of the seuententh conclusion, and then setting one foote of your compas in the centre, and extending the other foot vnto the edge of the arche or peece of the circumference, it is easy to drawe the whole circle.
Example.
A peece of an olde pillar was found, like in forme to thys figure A.D.B. Now to knowe howe muche the cõpasse of the hole piller was, seing by this parte it appereth that it was round, thus shal you do. Make in a table the like draught of yt circũference by the self patrõ, vsing it as it wer a croked ruler. F .iij. Then make .iij. prickes in that arche line, as I haue made, C. D. and E. And then finde out the common centre to them all, as the .xvij. conclusion teacheth. And that cẽtre is here F, nowe settyng one foote of your compas in F, and the other in C. D, other in E, and so makyng a compasse, you haue youre whole intent.
THE XXVI. CONCLVSION.
To finde the centre to any arche of a circle.
If so be it that you desire to find the centre by any other way then by those .iij. prickes, consideryng that sometimes you can not haue so much space in the thyng where the arche is drawen, as should serue to make those .iiij. bowe lines, then shall you do thus: Parte that arche line into two partes, equall other vnequall, it maketh no force, and vnto ech portion draw a corde, other a stringline. And then accordyng as you dyd in one arche in the .xvi. conclusion, so doe in bothe those arches here, that is to saie, deuide the arche in the middle, and also the corde, and drawe then a line by those two deuisions, so then are you sure that that line goeth by the centre. Afterward do lykewaies with the other arche and his corde, and where those .ij. lines do crosse, there is the centre, that you seke for.
Example.
The arche of the circle is A.B.C, vnto whiche I must seke [F.iii.v] a centre, therfore firste I do deuide it into .ij. partes, the one of them is A.B, and the other is B.C. Then doe I cut euery arche in the middle, so is E. the middle of A.B, and G. is the middle of B.C. Likewaies, I take the middle of their cordes, whiche I mark with F. and H, settyng F. by E, and H. by G. Then drawe I a line from E. to F, and from G. to H, and they do crosse in D, wherefore saie I, that D. is the centre, that I seke for.
THE XXVII. CONCLVSION.
To drawe a circle within a triangle appoincted.
For this conclusion and all other lyke, you muste vnderstande, that when one figure is named to be within an other, that it is not other waies to be vnderstande, but that eyther euery syde of the inner figure dooeth touche euerie corner of the other, other els euery corner of the one dooeth touche euerie side of the other. So I call that triangle drawen in a circle, whose corners do touche the circumference of the circle. And that circle is contained in a triangle, whose circumference doeth touche iustely euery side of the triangle, and yet dooeth not crosse ouer any side of it. And so that quadrate is called properly to be drawen in a circle, when all his fower angles doeth touche the edge of the circle, And that circle is drawen in a quadrate, whose circumference doeth touche euery side of the quadrate, and lykewaies of other figures.
[F.iiii.]| Examples are these. A.B.C.D.E.F. |
||
| A. is a circle in a triangle. |
C. a quadrate in a circle. |
|
 |
 |
 |
| B. a triangle in a circle. |
D. a circle in a quadrate. |
|
In these .ij. last figures E. and F, the circle is not named to be drawen in a triangle, because it doth not touche the sides of the triangle, neither is the triangle coũted to be drawen in the circle, because one of his corners doth not touche the circumference of the circle, yet (as you see) the circle is within the triangle, and the triangle within the circle, but nother of them is properly named to be in the other. Now to come to the conclusion. If the triangle haue all .iij. sides lyke, then shall you take the middle of euery side, and from the contrary corner drawe a right line vnto that poynte, and where those lines do crosse one an other, there is the centre. Then set one foote of the compas in the centre and stretche out the other to the middle pricke of any of the sides, and so drawe a compas, whiche shall touche euery side of the triangle, but shall not passe with out any of them.
Example.
The triangle is A.B.C, whose sides I do part into .ij. equall partes, eche by it selfe in these pointes D.E.F, puttyng F. betwene A.B, and D. betwene B.C, and E. betwene A.C. Then draw I a line from C. to F, and an other from A. to D, and the third from B. to E.
[F.iiii.v]And where all those lines do mete (that is to saie
M. G,) I set the one foote of
my compasse, because it is the common centre, and so drawe a circle
accordyng to the distaunce of any of the sides of the triangle. And then
find I that circle to agree iustely to all the sides of the triangle, so
that the circle is iustely made in the triangle, as the conclusion did
purporte. And this is euer true, when the triangle hath all thre sides
equall, other at the least .ij. sides lyke long. But in the other kindes
of triangles you must deuide euery angle in the middle, as the third
conclusion teaches you.
 And so drawe lines frõ eche angle to their middle pricke. And where
those lines do crosse, there is the common centre, from which you shall
draw a perpendicular to one of the sides. Then sette one foote of the
compas in that centre, and stretche the other foote accordyng to the
lẽgth of the perpendicular, and so drawe your circle.
And so drawe lines frõ eche angle to their middle pricke. And where
those lines do crosse, there is the common centre, from which you shall
draw a perpendicular to one of the sides. Then sette one foote of the
compas in that centre, and stretche the other foote accordyng to the
lẽgth of the perpendicular, and so drawe your circle.
Example.
The triangle is A.B.C, whose corners I haue diuided in the middle with D.E.F, and haue drawen the lines of diuision A.D, B.E, and C.F, which crosse in G, therfore shall G. be the common centre. Then make I one perpẽdicular from G. vnto the side B.C, and that G is G.H. Now sette I one fote of the compas in G, and extend the other foote vnto H. and so drawe a compas, whiche wyll iustly answere to that triãgle according to the meaning of the conclusion.
THE XXVIII. CONCLVSION.
To drawe a circle about any triãgle assigned.
Fyrste deuide two sides of the triangle equally in half and from those ij. prickes erect two perpendiculars, which muste needes meet in crosse, and that point of their meting is the centre of the circle that must be drawen, therefore sette one foote of the compasse in that pointe, and extend the other foote to one corner of the triangle, and so make a circle, and it shall touche all iij. corners of the triangle.
Example.
A.B.C. is the triangle, whose two sides A.C. and B.C. are diuided into two equall partes in D. and E, settyng D. betwene B. and C, and E. betwene A. and C. And from eche of those two pointes is ther erected a perpendicular (as you se D.F, and E.F.) which mete, and crosse in F, and stretche forth the other foot of any corner of the triangle, and so make a circle, that circle shal touch euery corner of the triangle, and shal enclose the whole triangle, accordinge, as the conclusion willeth.
An other way to do the same.
And yet an other waye may you doo it, accordinge as you learned in the seuententh conclusion, for if you call the three [G.i.v] corners of the triangle iij. prickes, and then (as you learned there) yf you seeke out the centre to those three prickes, and so make it a circle to include those thre prickes in his circumference, you shall perceaue that the same circle shall iustelye include the triangle proposed.
Example.
A.B.C. is the triangle, whose iij. corners I count to be iij. pointes. Then (as the seuentene conclusion doth teache) I seeke a common centre, on which I may make a circle, that shall enclose those iij prickes. that centre as you se is D, for in D. doth the right lines, that passe by the angles of the arche lines, meete and crosse. And on that centre as you se, haue I made a circle, which doth inclose the iij. angles of the triãgle, and consequentlye the triangle itselfe, as the conclusion dydde intende.
THE XXIX. CONCLVSION.
To make a triangle in a circle appoynted whose corners shal be equall to
the corners of any triangle assigned.
When I will draw a triangle in a circle appointed, so that the corners of that triangle shall be equall to the corners of any triangle assigned, then must I first draw a tuche lyne vnto that circle, as the twenty conclusion doth teach, and in the very poynte of the touche muste I make an angle, equall to one angle of the triangle, and that inwarde toward the circle: likewise in the same pricke must I make an other angle wt the other halfe of the touche line, equall to an other corner of the triangle appointed, and then betwen those two corners G.ij will there resulte a third angle, equall to the third corner of that triangle. Nowe where those two lines that entre into the circle, doo touche the circumference (beside the touche line) there set I two prickes, and betwene them I drawe a thyrde line. And so haue I made a triangle in a circle appointed, whose corners bee equall to the corners of the triangle assigned.
Example.
A.B.C, is the triangle appointed, and F.G.H. is the circle, in which I muste make an other triangle, with lyke angles to the angles of A.B.C. the triangle appointed. Therefore fyrst I make the touch lyne D.F.E. And then make I an angle in F, equall to A, whiche is one of the angles of the triangle. And the lyne that maketh that angle with the touche line, is F.H, whiche I drawe in lengthe vntill it touche the edge of the circle. Then againe in the same point F, I make an other corner equall to the angle C. and the line that maketh that corner with the touche line, is F.G. whiche also I drawe foorthe vntill it touche the edge of the circle. And then haue I made three angles vpon that one touch line, and in yt one point F, and those iij. angles be equall to the iij. angles of the triangle assigned, whiche thinge doth plainely appeare, in so muche as they bee equall [G.ii.v] to ij. right angles, as you may gesse by the fixt theoreme. And the thre angles of euerye triangle are equill also to ij. righte angles, as the two and twenty theoreme dothe show, so that bicause they be equall to one thirde thinge, they must needes be equal togither, as the cõmon sentence saith. Thẽ do I draw a line frome G. to H, and that line maketh a triangle F.G.H, whole angles be equall to the angles of the triangle appointed. And this triangle is drawn in a circle, as the conclusion didde wyll. The proofe of this conclusion doth appeare in the seuenty and iiij. Theoreme.
THE XXX. CONCLVSION.
To make a triangle about a circle assigned which shall haue corners,
equall to the corners of any triangle appointed.
First draw forth in length the one side of the triangle assigned so that therby you may haue ij. vtter angles, vnto which two vtter angles you shall make ij. other equall on the centre of the circle proposed, drawing thre halfe diameters frome the circumference, whiche shal enclose those ij. angles, thẽ draw iij. touche lines which shall make ij. right angles, eche of them with one of those semidiameters. Those iij. lines will make a triangle equally cornered to the triangle assigned, and that triangle is drawẽ about a circle apointed, as the cõclusiõ did wil.
Example.
A.B.C, is the triangle assigned, and G.H.K, is the circle appointed, about which I muste make a triangle hauing equall angles to the angles of that triangle A.B.C. Fyrst therefore I draw A.C. (which is one of the sides of the triangle) in length that there may appeare two vtter angles in that triangle, as you se B.A.D, and B.C.E.
G iij
Then drawe I in the circle appointed a semidiameter, which is here H.F, for F. is the cẽtre of the circle G.H.K. Then make I on that centre an angle equall to the vtter angle B.A.D, and that angle is H.F.K. Like waies on the same cẽtre by drawyng an other semidiameter, I make an other angle H.F.G, equall to the second vtter angle of the triangle, whiche is B.C.E. And thus haue I made .iij. semidiameters in the circle appointed. Then at the ende of eche semidiameter, I draw a touche line, whiche shall make righte angles with the semidiameter. And those .iij. touch lines mete, as you see, and make the trianagle L.M.N, whiche is the triangle that I should make, for it is drawen about a circle assigned, and hath corners equall to the corners of the triangle appointed, for the corner M. is equall to C. Likewaies L. to A, and N. to B, whiche thyng you shall better perceiue by the vi. Theoreme, as I will declare in the booke of proofes.
THE XXXI. CONCLVSION.
To make a portion of a circle on any right line assigned, whiche shall conteine an angle equall to a right lined angle appointed.
The angle appointed, maie be a sharpe angle, a right angle, other a blunte angle, so that the worke must be diuersely handeled [G.iii.v] according to the diuersities of the angles, but consideringe the hardenes of those seuerall woorkes, I wyll omitte them for a more meter time, and at this tyme wyll shewe you one light waye which serueth for all kindes of angles, and that is this. When the line is proposed, and the angle assigned, you shall ioyne that line proposed so to the other twoo lines contayninge the angle assigned, that you shall make a triangle of theym, for the easy dooinge whereof, you may enlarge or shorten as you see cause, anye of the two lynes contayninge the angle appointed. And when you haue made a triangle of those iij. lines, then accordinge to the doctrine of the seuẽ and twẽty coclusiõ, make a circle about that triangle. And so haue you wroughte the request of this conclusion. Whyche yet you maye woorke by the twenty and eight conclusion also, so that of your line appointed, you make one side of the triãgle be equal to ye ãgle assigned as youre selfe mai easily gesse.
Example.
First for example of a sharpe ãgle let A. stãd & B.C shal be ye lyne assigned. Thẽ do I make a triangle, by adding B.C, as a thirde side to those other ij. which doo include the ãgle assigned, and that triãgle is D.E.F, so yt E.F. [G.iiii.] is the line appointed, and D. is the angle assigned. Then doo I drawe a portion of a circle about that triangle, from the one ende of that line assigned vnto the other, that is to saie, from E. a long by D. vnto F, whiche portion is euermore greatter then the halfe of the circle, by reason that the angle is a sharpe angle. But if the angle be right (as in the second exaumple you see it) then shall the portion of the circle that containeth that angle, euer more be the iuste halfe of a circle. And when the angle is a blunte angle, as the thirde exaumple dooeth propounde, then shall the portion of the circle euermore be lesse then the halfe circle. So in the seconde example, G. is the right angle assigned, and H.K. is the lyne appointed, and L.M.N. the portion of the circle aunsweryng thereto. In the third exaumple, O. is the blunte corner assigned, P.Q. is the line, and R.S.T. is the portion of the circle, that containeth that blũt corner, and is drawen on R.T. the line appointed.
THE XXXII. CONCLVSION.
To cutte of from a circle appointed, a portion containyng an angle
equall to a right lyned angle assigned.
When the angle and the circle are assigned, first draw a touch line vnto that circle, and then drawe an other line from the pricke of the touchyng to one side of the circle, so that thereby those two lynes do make an angle equall to the angle assigned. Then saie I that the portion of the circle of the contrarie side to the angle drawen, is the parte that you seke for.
Example.
A. is the angle appointed, and D.E.F. is the circle assigned, frõ which I must cut away a portiõ that doth contain an angle [G.iiii.v] equall to this angle A. Therfore first I do draw a touche line to the circle assigned, and that touch line is B.C, the very pricke of the touche is D, from whiche D. I drawe a lyne D.E, so that the angle made of those two lines be equall to the angle appointed. Then say I, that the arch of the circle D.F.E, is the arche that I seke after. For if I doo deuide that arche in the middle (as here is done in F.) and so draw thence two lines, one to D, and the other to E, then will the angle F, be equall to the angle assigned.
THE XXXIII. CONCLVSION.
To make a square quadrate in a circle assigned.
Draw .ij. diameters in the circle, so that they runne a crosse, and that they make .iiij. right angles. Then drawe .iiij. lines, that may ioyne the .iiij. ends of those diameters, one to an other, and then haue you made a square quadrate in the circle appointed.
Example.
A.B.C.D. is the circle assigned, and A.C. and B.D. are the two diameters which crosse in the centre E, and make .iiij. right corners. Then do I make fowre other lines, that is A.B, B.C, C.D, and D.A, which do ioyne together the fowre endes of the ij. diameters. And so is the square H quadrate made in the circle assigned, as the conclusion willeth.
THE XXXIIII. CONCLVSION.
To make a square quadrate aboute annye circle assigned.
Drawe two diameters in crosse waies, so that they make foure righte angles in the centre. Then with your compasse take the length of the halfe diameter, and set one foote of the compas in eche end of the compas, so shall you haue viij. archelines. Then yf you marke the prickes wherin those arch lines do crosse, and draw betwene those iiij. prickes iiij right lines, then haue you made the square quadrate accordinge to the request of the conclusion.
Example.
A.B.C. is the circle assigned in which first I draw two diameters, in crosse waies, making iiij. righte angles, and those ij. diameters are A.C. and B.D. Then sette I my compasse (whiche is opened according to the semidiameter of the said circle) fixing one foote in the end of euery semidiameter, and drawe with the other foote twoo arche lines, one on euery side. As firste, when I sette the one foote in A, [H.i.v] then with the other foote I doo make twoo arche lines, one in E, and an other in F. Then sette I the one foote of the compasse in B, and drawe twoo arche lines F. and G. Like wise setting the compasse foote in C, I drawe twoo other arche lines, G. and H, and on D. I make twoo other, H. and E. Then frome the crossinges of those eighte arche lines I drawe iiij. straighte lynes, that is to saye, E.F, and F.G, also G.H, and H.E, whiche iiij. straighte lynes do make the square quadrate that I should draw about the circle assigned.
THE XXXV. CONCLVSION.
To draw a circle in any square quadrate appointed.
Fyrste deuide euery side of the quadrate into twoo equall partes, and so drawe two lynes betwene eche two contrary poinctes, and where those twoo lines doo crosse, there is the centre of the circle. Then sette the foote of the compasse in that point, and stretch forth the other foot, according to the length of halfe one of those lines, and so make a compas in the square quadrate assigned.
Example.
A.B.C.D. is the quadrate appointed, in whiche I muste make a circle. Therefore first I do deuide euery side in ij. equal partes, and draw ij. lines acrosse, betwene eche ij. cõtrary prickes, as you se E.G, and F.H, whiche mete in K, and therfore shal K, be the centre of the circle. Then do I set one foote of the compas in K. and opẽ the other as wide as K.E, and so draw a circle, which is made accordinge to the conclusion.
H.ij.
THE XXXVI. CONCLVSION.
To draw a circle about a square quadrate.
Draw ij. lines betwene the iiij. corners of the quadrate, and where they mete in crosse, ther is the centre of the circle that you seeke for. Thẽ set one foot of the compas in that centre, and extend the other foote vnto one corner of the quadrate, and so may you draw a circle which shall iustely inclose the quadrate proposed.
Example.
A.B.C.D. is the square quadrate proposed, about which I must make a circle. Therfore do I draw ij. lines crosse the square quadrate from angle to angle, as you se A.C. & B.D. And where they ij. do crosse (that is to say in E.) there set I the one foote of the compas as in the centre, and the other foote I do extend vnto one angle of the quadrate, as for exãple to A, and so make a compas, whiche doth iustly inclose the quadrate, according to the minde of the conclusion.
THE XXXVII. CONCLVSION.
To make a twileke triangle, whiche shall haue euery of the ij. angles that lye about the ground line, double to the other corner.
Fyrste make a circle, and deuide the circumference of it into fyue equall partes. And thenne drawe frome one pricke (which you will) two lines to ij. other prickes, that is to say to the iij. and iiij. pricke, counting that for the first, wherhence you drewe both those lines, Then drawe the thyrde lyne to make a triangle with those other twoo, and you haue doone according to the conclusion, and haue made a twelike triãgle, [H.ii.v] whose ij. corners about the grounde line, are eche of theym double to the other corner.
At no point in this or the accompanying book does the author show how to divide a circle into five.
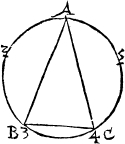
Example.
A.B.C. is the circle, whiche I haue deuided into fiue equal portions. And from one of the prickes (which is A,) I haue drawẽ ij. lines, A.B. and B.C, whiche are drawen to the third and iiij. prickes. Then draw I the third line C.B, which is the grounde line, and maketh the triangle, that I would haue, for the ãgle C. is double to the angle A, and so is the angle B. also.
THE XXXVIII. CONCLVSION.
To make a cinkangle of equall sides, and equall corners in any circle
appointed.
Deuide the circle appointed into fiue equall partes, as you didde in the laste conclusion, and drawe ij. lines from euery pricke to the other ij. that are nexte vnto it. And so shall you make a cinkangle after the meanynge of the conclusion.
Example.
Yow se here this circle A.B.C.D.E. deuided into fiue equall portions. And from eche pricke ij. lines drawen to the other ij. nexte prickes, so from A. are drawen ij. lines, one to B, and the other to E, and so from C. one to B. and an other H.iij. to D, and likewise of the reste. So that you haue not only learned hereby how to make a sinkangle in anye circle, but also how you shal make a like figure spedely, whanne and where you will, onlye drawinge the circle for the intente, readylye to make the other figure (I meane the cinkangle) thereby.
THE XXXIX. CONCLVSION.
How to make a cinkangle of equall sides and equall angles about any
circle appointed.
Deuide firste the circle as you did in the last conclusion into fiue equall portions, and draw fiue semidiameters in the circle. Then make fiue touche lines, in suche sorte that euery touche line make two right angles with one of the semidiameters. And those fiue touche lines will make a cinkangle of equall sides and equall angles.
Example.
A.B.C.D.E. is the circle appointed, which is deuided into fiue equal partes. And vnto euery prycke is drawẽ a semidiameter, as you see. Then doo I make a touche line in the pricke B, whiche is F.G, making ij. right angles [H.iii.v] with the semidiameter B, and lyke waies on C. is made G.H, on D. standeth H.K, and on E, is set K.L, so that of those .v. touche lynes are made the .v. sides of a cinkeangle, accordyng to the conclusion.
An other waie.
Another waie also maie you drawe a cinkeangle aboute a circle, drawyng first a cinkeangle in the circle (whiche is an easie thyng to doe, by the doctrine of the .xxxvij. conclusion) and then drawing .v. touche lines whiche shall be iuste paralleles to the .v. sides of the cinkeangle in the circle, forseeyng that one of them do not crosse ouerthwarte an other and then haue you done. The exaumple of this (because it is easie) I leaue to your owne exercise.
THE XL. CONCLVSION.
To make a circle in any appointed cinkeangle of equall sides and equall
corners.
Drawe a plumbe line from any one corner of the cinkeangle, vnto the middle of the side that lieth iuste against that angle. And do likewaies in drawyng an other line from some other corner, to the middle of the side that lieth against that corner also. And those two lines wyll meete in crosse in the pricke of their crossyng, shall you iudge the centre of the circle to be. Therfore set one foote of the compas in that pricke, and extend the other to the end of the line that toucheth the middle of one side, whiche you liste, and so drawe a circle. And it shall be iustly made in the cinkeangle, according to the conclusion.
Example.
The cinkeangle assigned is A.B.C.D.E, in whiche I muste [H.iiii.] make a circle, wherefore I draw a right line from the one angle (as from B,) to the middle of the contrary side (whiche is E. D,) and that middle pricke is F. Then lykewaies from an other corner (as from E) I drawe a right line to the middle of the side that lieth against it (whiche is B.C.) and that pricke is G. Nowe because that these two lines do crosse in H, I saie that H. is the centre of the circle, whiche I would make. Therfore I set one foote of the compasse in H, and extend the other foote vnto G, or F. (whiche are the endes of the lynes that lighte in the middle of the side of that cinkeangle) and so make I the circle in the cinkangle, right as the cõclusion meaneth.
THE XLI. CONCLVSION
To make a circle about any assigned cinkeangle of equall sides, and
equall corners.
Drawe .ij. lines within the cinkeangle, from .ij. corners to the middle on tbe .ij. contrary sides (as the last conclusion teacheth) and the pointe of their crossyng shall be the centre of the circle that I seke for. Then sette I one foote of the compas in that centre, and the other foote I extend to one of the angles of the cinkangle, and so draw I a circle about the cinkangle assigned.
Example.
A.B.C.D.E, is the cinkangle assigned, about which I would make a circle. Therfore I drawe firste of all two lynes (as you see) one frõ E. to G, and the other frõ C. to F, and because thei do [H.iiii.v] meete in H, I saye that H. is the centre of the circle that I woulde haue, wherfore I sette one foote of the compasse in H. and extende the other to one corner (whiche happeneth fyrste, for all are like distaunte from H.) and so make I a circle aboute the cinkeangle assigned.
An other waye also.
Another waye maye I do it, thus presupposing any three corners of the cinkangle to be three prickes appointed, vnto whiche I shoulde finde the centre, and then drawinge a circle touchinge them all thre, accordinge to the doctrine of the seuentene, one and twenty, and two and twenty conclusions. And when I haue founde the centre, then doo I drawe the circle as the same conclusions do teache, and this forty conclusion also.
THE XLII. CONCLVSION.
To make a siseangle of equall sides, and equall angles, in any circle
assigned.
Yf the centre of the circle be not knowen, then seeke oute the centre according to the doctrine of the sixtenth conclusion. And with your compas take the quantitee of the semidiameter iustly. And then sette one foote in one pricke of the I.i. circũference of the circle, and with the other make a marke in the circumference also towarde both sides. Then sette one foote of the compas stedily in eche of those new prickes, and point out two other prickes. And if you haue done well, you shal perceaue that there will be but euen sixe such diuisions in the circumference. Whereby it dothe well appeare, that the side of anye sisangle made in a circle, is equalle to the semidiameter of the same circle.
Example.
The circle is B.C.D.E.F.G, whose centre I finde to bee A. Therefore I sette one foote of the compas in A, and do extẽd the other foote to B, thereby takinge the semidiameter. Then sette I one foote of the compas vnremoued in B, and marke with the other foote on eche side C. and G. Then from C. I marke D, and frõ D, E: from E. marke I F. And then haue I but one space iuste vnto G. and so haue I made a iuste siseangle of equall sides and equall angles, in a circle appointed.
THE XLIII. CONCLVSION.
To make a siseangle of equall sides, and equall angles about any circle
assigned.
THE XLIIII. CONCLVSION.
To make a circle in any siseangle appointed, of equall sides and equal
angles.
[I.i.v]
THE XLV. CONCLVSION.
To make a circle about any sise angle limited of equall sides and equall
angles.
Bicause you maye easily coniecture the makinge of these figures by that that is saide before of cinkangles, only consideringe that there is a difference in the numbre of sides, I thought beste to leue these vnto your owne deuice, that you should study in some thinges to exercise your witte withall and that you mighte haue the better occasion to perceaue what difference there is betwene eche twoo of those conclusions. For thoughe it seeme one thing to make a siseangle in a circle, and to make a circle about a siseangle, yet shall you perceaue, that is not one thinge, nother are those twoo conclusions wrought one way. Likewaise shall you thinke of those other two conclusions. To make a siseangle about a circle, and to make a circle in a siseangle, thoughe the figures be one in fashion, when they are made, yet are they not one in working, as you may well perceaue by the xxxvij. xxxviij. xxxix. and xl. conclusions, in whiche the same workes are taught, touching a circle and a cinkangle, yet this muche wyll I saye, for your helpe in working, that when you shall seeke the centre in a siseangle (whether it be to make a circle in it other about it) you shall drawe the two crosselines, from one angle to the other angle that lieth againste it, and not to the middle of any side, as you did in the cinkangle.
THE XLVI. CONCLVSION.
To make a figure of fifteene equall sides and angles in any circle
appointed.
This rule is generall, that how many sides the figure shall
[I.ii.]
haue, that shall be drawen in any circle, into so many partes iustely
muste the circles bee deuided. And therefore it is the more easier
woorke commonly, to drawe a figure in a circle, then to make a circle in
an other figure. Now therefore to end this conclusion, deuide the circle
firste into fiue partes, and
then eche of them into three partes againe: Or els
first deuide it into three partes, and then ech
of thẽ into fiue other partes, as you
list, and canne most readilye.
Then draw lines betwene
euery two prickes
that be
nighest
togither, and
ther wil appear rightly drawẽ the figure, of fiftene sides, and
angles equall. And so do with any other figure
of what numbre of sides so euer it bee.
FINIS.
[a.i.]

[a.i.v]
If truthe maie trie it selfe,
By Reasons prudent skyll,
If reason maie preuayle by right,
And rule the rage of will,
I dare the triall byde,
For truthe that I pretende.
And though some lyst at me repine,
Iuste truthe shall me defende.
THE PREFACE VNTO
the Theoremes.
 Doubt not gentle reader, but as my argument is straunge and vnacquainted
with the vulgare toungue, so shall I of many men be straungly talked of,
and as straungly iudged. Some men will saye peraduenture, I mighte
haue better imployed my tyme in some pleasaunte historye, comprisinge
matter of chiualrye. Some other wolde more haue preised my trauaile, if
I hadde spente the like time in some morall matter, other in deciding some
controuersy of religion. And yet some men (as I iudg) will not mislike
this kind of mater, but then will they wishe that I had vsed a more
certaine order in placinge bothe the Propositions and Theoremes, and
also a more exacter proofe of eche of theim bothe, by demonstrations
mathematicall. Some also will mislike my shortenes and simple plainesse,
as other of other affections diuersely shall espye somwhat that they
shall thinke blame worthy, and shal misse somewhat, that thei wold with
to haue bene here vsed, so that euerie manne shall giue his verdicte of
me according to his phantasie, vnto whome ioinctly, I make this my
firste answere: that as they ar many and in opinions verie diuers, so
were it scarse possible to please them all with anie one argumente, of
what kinde so euer it were. And for my seconde aunswere, I saye
thus. That if annye one argumente mighte please them all, then should
thei be thankfull vnto me for this kind of matter. For nother is there
anie matter more straunge in the englishe tungue, then this whereof
neuer booke was written before now, in that tungue, and therefore oughte
to delite all them, that desire to vnderstand strange matters, as most
men commonlie doo. And againe the practise is so pleasaunt in vsinge,
and so profitable in appliynge, that who so euer dothe
[a.ii.v]
delite in anie of bothe, ought not of right to mislike this arte. And if
any manne shall like the arte welle for it selfe, but shall mislyke the
fourme that I haue vsed in teachyng of it, to hym I shall saie, Firste,
that I dooe wishe with hym that some other man, whiche coulde better
haue doone it, hadde shewed his good will, and vsed his diligence in
suche sorte, that I myght haue bene therby occasioned iustely to haue
left of my laboure, or after my trauaile to haue suppressed my bookes.
But sithe no manne hath yet attempted the like, as far as I canne
learne, I truste all suche as bee not exercised in the studie of
Geometrye, shall finde greate ease and furtheraunce by this simple,
plaine, and easie forme of writinge. And shall perceaue the exacte
woorkes of Theon, and others that write on Euclide, a great deale
the soner,
by this blunte delineacion afore hande to them taughte. For I dare
presuppose of them, that thing which I haue sette in my selfe, and haue
marked in others, that is to saye, that it is not easie for a man that
shall trauaile in a straunge arte, to vnderstand at the beginninge bothe
the thing that is taught and also the iuste reason whie it is so. And by
experience of teachinge I haue tried it to bee true, for whenne I haue
taughte the proposition, as it is imported in meaninge, and annexed the
demonstration with all, I didde perceaue that it was a greate
trouble and a painefull vexacion of mynde to the learner, to comprehend
bothe those thinges at ones. And therfore did I proue firste to make
them to vnderstande the sence of the propositions, and then afterward
did they conceaue the demonstrations muche soner, when they hadde the
sentence of the propositions first ingrafted in their mindes. This
thinge caused me in bothe these bookes to omitte the demonstrations, and
to vse onlye a plaine forme of declaration, which might best serue for
the firste introduction. Whiche example hath beene vsed by other learned menne before
nowe, for not only Georgius Ioachimus Rheticus, but also Boetius that
wittye clarke did set forth some whole books of Euclide, without any
demonstration or any
a.iij.
other declaratiõ at al. But & if I shal hereafter perceaue that it
maie be a thankefull trauaile to sette foorth the propositions of
geometrie with demonstrations, I will not refuse to dooe it, and
that with sundry varietees of demonstrations, bothe pleasaunt and
profitable also. And then will I in like maner prepare to sette foorth
the other bookes, whiche now are lefte vnprinted, by occasion not so
muche of the charges in cuttyng of the figures, as for other iuste
hynderances, whiche I truste hereafter shall bee remedied. In the meane
season if any man muse why I haue sette the Conclusions beefore the
Teoremes, seynge many of the Theoremes seeme to include the cause of
some of the conclusions, and therfore oughte to haue gone before them,
as the cause goeth before the effecte. Here vnto I saie, that although
the cause doo go beefore the effect in order of nature, yet in order of
teachyng the effect must be fyrst declared, and than the cause therof
shewed, for so that men best vnderstãd things First to lerne that such
thinges ar to be wrought, and secondarily what thei ar, and what thei do
import, and thã thirdly what is the cause therof. An other cause why
yt the theoremes be put after the cõclusions is this, whã I
wrote these first cõnclusions (which was .iiiij. yeres passed)
I thought not then to haue added any theoremes, but next vnto
ye cõclusiõs to haue taught the order how to haue applied thẽ
to work, for drawing of plottes & such like vses. But afterward
cõsidering the great cõmoditie yt thei serue for, and the
light that thei do geue to all sortes of practise geometricall, besyde
other more notable benefites, whiche shall be declared more specially in
a place conuenient, I thoughte beste to geue you some taste of
theym, and the pleasaunt contemplation of suche geometrical
propositions, which might serue diuerselye in other bookes for the
demonstrations and proofes of all Geometricall woorkes. And in theim, as
well as in the propositions, I haue drawen in the Linearie examples
many tymes more lynes, than be spoken of in the explication of them,
whiche is doone to this intent, that yf any manne lyst to learne the
demonstrations by harte, (as somme
[a.iii.v]
learned men haue iudged beste to doo) those same men should find the
Linearye exaumples to serue for this purpose, and to wante no thyng
needefull to the iuste proofe, whereby this booke may bee wel approued
to be more complete then many men wolde suppose it.
Doubt not gentle reader, but as my argument is straunge and vnacquainted
with the vulgare toungue, so shall I of many men be straungly talked of,
and as straungly iudged. Some men will saye peraduenture, I mighte
haue better imployed my tyme in some pleasaunte historye, comprisinge
matter of chiualrye. Some other wolde more haue preised my trauaile, if
I hadde spente the like time in some morall matter, other in deciding some
controuersy of religion. And yet some men (as I iudg) will not mislike
this kind of mater, but then will they wishe that I had vsed a more
certaine order in placinge bothe the Propositions and Theoremes, and
also a more exacter proofe of eche of theim bothe, by demonstrations
mathematicall. Some also will mislike my shortenes and simple plainesse,
as other of other affections diuersely shall espye somwhat that they
shall thinke blame worthy, and shal misse somewhat, that thei wold with
to haue bene here vsed, so that euerie manne shall giue his verdicte of
me according to his phantasie, vnto whome ioinctly, I make this my
firste answere: that as they ar many and in opinions verie diuers, so
were it scarse possible to please them all with anie one argumente, of
what kinde so euer it were. And for my seconde aunswere, I saye
thus. That if annye one argumente mighte please them all, then should
thei be thankfull vnto me for this kind of matter. For nother is there
anie matter more straunge in the englishe tungue, then this whereof
neuer booke was written before now, in that tungue, and therefore oughte
to delite all them, that desire to vnderstand strange matters, as most
men commonlie doo. And againe the practise is so pleasaunt in vsinge,
and so profitable in appliynge, that who so euer dothe
[a.ii.v]
delite in anie of bothe, ought not of right to mislike this arte. And if
any manne shall like the arte welle for it selfe, but shall mislyke the
fourme that I haue vsed in teachyng of it, to hym I shall saie, Firste,
that I dooe wishe with hym that some other man, whiche coulde better
haue doone it, hadde shewed his good will, and vsed his diligence in
suche sorte, that I myght haue bene therby occasioned iustely to haue
left of my laboure, or after my trauaile to haue suppressed my bookes.
But sithe no manne hath yet attempted the like, as far as I canne
learne, I truste all suche as bee not exercised in the studie of
Geometrye, shall finde greate ease and furtheraunce by this simple,
plaine, and easie forme of writinge. And shall perceaue the exacte
woorkes of Theon, and others that write on Euclide, a great deale
the soner,
by this blunte delineacion afore hande to them taughte. For I dare
presuppose of them, that thing which I haue sette in my selfe, and haue
marked in others, that is to saye, that it is not easie for a man that
shall trauaile in a straunge arte, to vnderstand at the beginninge bothe
the thing that is taught and also the iuste reason whie it is so. And by
experience of teachinge I haue tried it to bee true, for whenne I haue
taughte the proposition, as it is imported in meaninge, and annexed the
demonstration with all, I didde perceaue that it was a greate
trouble and a painefull vexacion of mynde to the learner, to comprehend
bothe those thinges at ones. And therfore did I proue firste to make
them to vnderstande the sence of the propositions, and then afterward
did they conceaue the demonstrations muche soner, when they hadde the
sentence of the propositions first ingrafted in their mindes. This
thinge caused me in bothe these bookes to omitte the demonstrations, and
to vse onlye a plaine forme of declaration, which might best serue for
the firste introduction. Whiche example hath beene vsed by other learned menne before
nowe, for not only Georgius Ioachimus Rheticus, but also Boetius that
wittye clarke did set forth some whole books of Euclide, without any
demonstration or any
a.iij.
other declaratiõ at al. But & if I shal hereafter perceaue that it
maie be a thankefull trauaile to sette foorth the propositions of
geometrie with demonstrations, I will not refuse to dooe it, and
that with sundry varietees of demonstrations, bothe pleasaunt and
profitable also. And then will I in like maner prepare to sette foorth
the other bookes, whiche now are lefte vnprinted, by occasion not so
muche of the charges in cuttyng of the figures, as for other iuste
hynderances, whiche I truste hereafter shall bee remedied. In the meane
season if any man muse why I haue sette the Conclusions beefore the
Teoremes, seynge many of the Theoremes seeme to include the cause of
some of the conclusions, and therfore oughte to haue gone before them,
as the cause goeth before the effecte. Here vnto I saie, that although
the cause doo go beefore the effect in order of nature, yet in order of
teachyng the effect must be fyrst declared, and than the cause therof
shewed, for so that men best vnderstãd things First to lerne that such
thinges ar to be wrought, and secondarily what thei ar, and what thei do
import, and thã thirdly what is the cause therof. An other cause why
yt the theoremes be put after the cõclusions is this, whã I
wrote these first cõnclusions (which was .iiiij. yeres passed)
I thought not then to haue added any theoremes, but next vnto
ye cõclusiõs to haue taught the order how to haue applied thẽ
to work, for drawing of plottes & such like vses. But afterward
cõsidering the great cõmoditie yt thei serue for, and the
light that thei do geue to all sortes of practise geometricall, besyde
other more notable benefites, whiche shall be declared more specially in
a place conuenient, I thoughte beste to geue you some taste of
theym, and the pleasaunt contemplation of suche geometrical
propositions, which might serue diuerselye in other bookes for the
demonstrations and proofes of all Geometricall woorkes. And in theim, as
well as in the propositions, I haue drawen in the Linearie examples
many tymes more lynes, than be spoken of in the explication of them,
whiche is doone to this intent, that yf any manne lyst to learne the
demonstrations by harte, (as somme
[a.iii.v]
learned men haue iudged beste to doo) those same men should find the
Linearye exaumples to serue for this purpose, and to wante no thyng
needefull to the iuste proofe, whereby this booke may bee wel approued
to be more complete then many men wolde suppose it.
And thus for this tyme I wyll make an ende without any larger declaration of the commoditiees of this arte, or any farther answeryng to that may bee obiected agaynst my handelyng of it, wyllyng them that myslike it, not to medle with it: and vnto those that will not disdaine the studie of it, I promise all suche aide as I shall be able to shewe for their farther procedyng both in the same, and in all other commoditees that thereof maie ensue. And for their incouragement I haue here annexed the names and brefe argumentes of suche bookes, as I intende (God willyng) shortly to sette forth, if I shall perceaue that my paynes maie profyte other, as my desyre is.
The brefe argumentes of suche bokes as ar appoynted shortly to be set forth by the author herof.
The seconde part of Arithmetike, teachyng the workyng by fractions, with extraction of rootes both square and cubike: And declaryng the rule of allegation, with sundrye plesaunt exaumples in metalles and other thynges. Also the rule of false position, with dyuers examples not onely vulgar, but some appertaynyng to the rule of Algeber, applied vnto quantitees partly rationall, and partly surde.
The arte of Measuryng by the quadrate geometricall, and the disorders committed by vsyng the same, not only reueled but reformed also (as muche as to the instrument pertayneth) by the deuise of a new quadrate newely inuented by the author hereof.
The arte of measuryng by the astronomers staffe, and by the astronomers ryng, and the form of makyng them both.
The arte of makyng of Dials, bothe for the daie and the nyght, with certayn new formes of fixed dialles for the moon [a.iiii.] and other for the sterres, whiche may bee sette in glasse windowes to serue by daie and by night. And howe you may by those dialles knowe in what degree of the Zodiake not only the sonne, but also the moone is. And how many howrs old she is. And also by the same dial to know whether any eclipse shall be that moneth, of the sonne or of the moone.
The makyng and vse of an instrument, wherby you maye not onely measure the distance at ones of all places that you can see togyther, howe muche eche one is from you, and euery one from other, but also therby to drawe the plotte of any countreie that you shall come in, as iustely as maie be, by mannes diligence and labour.
The vse bothe of the Globe and the Sphere, and therin also of the arte of Nauigation, and what instrumentes serue beste thervnto, and of the trew latitude and longitude of regions and townes.
Euclides woorkes in foore partes, with diuers demonstrations Arithmeticall and Geometricall or Linearie. The fyrst parte of platte formes. The second of numbres and quantitees surde or irrationall. The third of bodies and solide formes. The fourthe of perspectiue, and other thynges thereto annexed.
BESIDE these I haue other sundrye woorkes partely ended, and partely to bee ended, Of the peregrination of man, and the originall of al nations, The state of tymes, and mutations of realmes, The image of a perfect common welth, with diuers other woorkes in naturall sciences, Of the wonderfull workes and effectes in beastes, plantes, and minerals, of whiche at this tyme, I will omitte the argumentes, beecause thei doo appertaine littel to this arte, and handle other matters in an other sorte.
To haue, or leaue,
Nowe maie you chuse,
No paine to please,
Will I refuse.
That frõ any pricke to one other, there may be drawen a right line.
 s for example
s for example ![]() A. being the one pricke, and B. the
other, you maye drawe betwene them from the one to the other, that is to
say, frome A. vnto B, and from B.
to A.
A. being the one pricke, and B. the
other, you maye drawe betwene them from the one to the other, that is to
say, frome A. vnto B, and from B.
to A.
That any right line of measurable length may be drawen forth longer, and straight.
![]()
Example of A.B, which as it is a line of measurable lengthe, so may it be drawen forth farther, as for example vnto C, and that in true streightenes without crokinge.
III.
That vpon any centre, there may be made a circle of anye quãtitee that a man wyll.
Let the centre be set to be A, what shal hinder a man to drawe a circle aboute it, of what quantitee that he lusteth, as you se the forme here: other bygger or lesse, as it shall lyke him to doo:
[b.i.v]That all right angles be equall eche to other.
Set for an example A. and B, of which two though A. seme the greatter angle to some men of small experience, it happeneth only bicause that the lines aboute A, are longer thẽ the lines about B, as you may proue by drawing them longer, for so that B. seme the greater angle yf you make his lines longer then the lines that make the angle A. And to proue it by demonstration, I say thus. If any ij. right corners be not equal, then one right corner is greater then an other, but that corner which is greatter then a right angle, is a blunt corner (by his definition) so must one corner be both a right corner and a blunt corner also, which is not possible: And againe: the lesser right corner must be a sharpe corner, by his definition, bicause it is lesse then a right angle. which thing is impossible. Therefore I conclude that all right angles be equall.
Yf one right line do crosse two other right lines, and make ij. inner corners of one side lesser thẽ ij. righte corners, it is certaine, that if those two lines be drawen forth right on that side that the sharpe inner corners be, they wil at lẽgth mete togither, and crosse on an other.
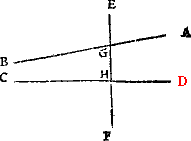
The ij. lines beinge as A.B. and C.D, and the third line crossing them as dooth heere E.F, making ij inner cornes (as ar G.H.) lesser then two right corners, sith ech of b.ij. them is lesse then a right corner, as your eyes maye iudge, then say I, if those ij. lines A.B. and C.D. be drawen in lengthe on that side that G. and H. are, the will at length meet and crosse one an other.
Two right lines make no platte forme.
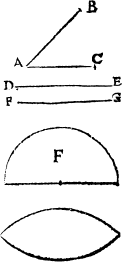
A platte forme, as you harde before, hath bothe length and bredthe, and is inclosed with lines as with his boundes, but ij. right lines cannot inclose al the bondes of any platte forme. Take for an example firste these two right lines A.B. and A.C. whiche meete togither in A, but yet cannot be called a platte forme, bicause there is no bond from B. to C, but if you will drawe a line betwene them twoo, that is frome B. to C, then will it be a platte forme, that is to say, a triangle, but then are there iij. lines, and not only ij. Likewise may you say of D.E. and F.G, whiche doo make a platte forme, nother yet can they make any without helpe of two lines more, whereof the one must be drawen from D. to F, and the other frome E. to G, and then will it be a longe rquare. So then of two right lines can bee made no platte forme. But of ij. croked lines be made a platte forme, as you se in the eye form. And also of one right line, & one croked line, maye a platte fourme bee made, as the semicircle F. doothe sette forth.
[b.ii.v]
Certayn common sentences manifest to
sence, and acknowledged of all men.
The firste common sentence.
What so euer things be equal to one other thinge, those same bee equall betwene them selues.
Examples therof you may take both in greatnes and also in numbre. First (though it pertaine not proprely to geometry, but to helpe the vnderstandinge of the rules, whiche may bee wrought by bothe artes) thus may you perceaue. If the summe of monnye in my purse, and the mony in your purse be equall eche of them to the mony that any other man hathe, then must needes your mony and mine be equall togyther. Likewise, if anye ij. quantities, as A. and B, be equal to an other, as vnto C, then muste nedes A. and B. be equall eche to other, as A. equall to B, and B. equall to A, whiche thinge the better to perceaue, tourne these quantities into numbre, so shall A. and B. make sixteene, and C. as many. As you may perceaue by multipliyng the numbre of their sides togither.
The seconde common sentence.
And if you adde equall portions to thinges that be equall, what so amounteth of them b.iij. shall be equall.
Example, Yf you and I haue like summes of mony, and then receaue eche of vs like summes more, then our summes wil be like styll. Also if A. and B. (as in the former example) bee equall, then by adding an equal portion to them both, as to ech of them, the quarter of A. (that is foure) they will be equall still.
The thirde common sentence.
And if you abate euen portions from things that are equal, those partes that remain shall be equall also.
This you may perceaue by the last example. For that that was added there, is subtracted heere. and so the one doothe approue the other.
The fourth common sentence.
If you abate equalle partes from vnequal thinges, the remainers shall be vnequall.
As bicause that a hundreth and eight and forty be vnequal if I take tenne from them both, there will remaine nynetye and eight and thirty, which are also vnequall. and likewise in quantities it is to be iudged.
The fifte common sentence.
When euen portions are added to vnequalle thinges, those that amounte shalbe vnequall.
[b.iii.v]So if you adde twenty to fifty, and lyke ways to nynty, you shall make seuenty and a hundred and ten whiche are no lesse vnequall, than were fifty and nynty.
The syxt common sentence.
If two thinges be double to any other, those same two thinges are equal togither.
Bicause A. and B. are eche of them double to C, therefore must A. and B. nedes be equall togither. For as v. times viij. maketh xl. which is double to iiij. times v, that is xx so iiij. times x, likewise is double to xx. (for it maketh fortie) and therefore muste neades be equall to forty.
The seuenth common sentence.
If any two thinges be the halfes of one other thing, then are thei .ij. equall togither.
So are D. and C. in the laste example equal togyther, bicause they are eche of them the halfe of A. other of B, as their numbre declareth.
The eyght common sentence.
If any one quantitee be laide on an other, and thei agree, so that the one [b.iiii.] excedeth not the other, then are they equall togither.
As if this figure A.B.C, be layed on that other D.E.F, so that A. be layed to D, B. to E, and C. to F, you shall see them agre in sides exactlye and the one not to excede the other, for the line A.B. is equall to D.E, and the third lyne C.A, is equall to F.D so that eueryside in the one is equall to some one side of the other. Wherfore it is playne, that the two triangles are equall togither.
The nynth common sentence.
Euery whole thing is greater than any of his partes.
This sentence nedeth none example. For the thyng is more playner then any declaration, yet considering that other common sentence that foloweth nexte that.
The tenthe common sentence.
Euery whole thinge is equall to all his partes taken togither.
It shall be mete to expresse both wt one example, for of
thys last sentence many mẽ at the first hearing do make a doubt.
Therfore as in this example of the circle deuided into sũdry partes
[b.iiii.v]
it doeth appere that no parte can be so great as the whole circle,
(accordyng to the meanyng of the eight sentence) so yet it is certain,
that all those eight partes together be equall vnto the whole circle.
And this is the meanyng of that common sentence (whiche many vse, and
fewe do rightly vnderstand) that is, that All the partes of any
thing are nothing els, but the whole. And contrary waies: The
whole is nothing els, but all his partes taken togither. whiche
saiynges some haue vnderstand to meane thus: that all the partes are of
the same kind that the whole thyng is:
 but that that meanyng is false, it doth plainly appere by this figure
A.B, whose partes A. and B, are triangles,
and the whole figure is a square, and so are they not of one kind. But
and if they applie it to the matter or substance of thinges (as some do)
then it is most false, for euery compound thyng is made of partes of
diuerse matter and substance. Take for example a man, a house,
a boke, and all other compound thinges. Some vnderstand it thus,
that the partes all together can make none other forme, but that that
the whole doth shewe, whiche is also false, for I maie make fiue hundred
diuerse figures of the partes of some one figure, as you shall better
perceiue in the third boke.
but that that meanyng is false, it doth plainly appere by this figure
A.B, whose partes A. and B, are triangles,
and the whole figure is a square, and so are they not of one kind. But
and if they applie it to the matter or substance of thinges (as some do)
then it is most false, for euery compound thyng is made of partes of
diuerse matter and substance. Take for example a man, a house,
a boke, and all other compound thinges. Some vnderstand it thus,
that the partes all together can make none other forme, but that that
the whole doth shewe, whiche is also false, for I maie make fiue hundred
diuerse figures of the partes of some one figure, as you shall better
perceiue in the third boke.
 And in the meane seasõ take for an exãple this square figure following
A.B.C.D, wch is deuided but in two parts, and yet
(as you se) I haue made fiue figures more beside the firste, with
onely diuerse ioynyng of those two partes. But of this shall I speake
more largely in an other place. In the mean season content your self with these
principles, whiche are certain of the chiefe groundes wheron all
demonstrations mathematical are fourmed, of which though the moste parte
seeme so plaine, that no childe doth doubte of them, thinke not therfore
that the art vnto whiche they serue, is simple, other childishe, but
rather consider, howe certayne
c.
the profes of that arte is, yt hath for his groũdes soche
playne truthes, & as I may say, suche vndowbtfull and sensible principles, And this
is the cause why all learned menne dooth approue the certenty of
geometry, and cõsequently of the other artes mathematical, which haue
the grounds (as Arithmeticke, musike and astronomy) aboue all other
artes and sciences, that be vsed amõgest men. Thus muche haue I sayd of
the first principles, and now will I go on with the theoremes, whiche I
do only by examples declare, minding to reserue the proofes to a peculiar
boke which I will then set forth, when I perceaue this to be thankfully
taken of the readers of it.
And in the meane seasõ take for an exãple this square figure following
A.B.C.D, wch is deuided but in two parts, and yet
(as you se) I haue made fiue figures more beside the firste, with
onely diuerse ioynyng of those two partes. But of this shall I speake
more largely in an other place. In the mean season content your self with these
principles, whiche are certain of the chiefe groundes wheron all
demonstrations mathematical are fourmed, of which though the moste parte
seeme so plaine, that no childe doth doubte of them, thinke not therfore
that the art vnto whiche they serue, is simple, other childishe, but
rather consider, howe certayne
c.
the profes of that arte is, yt hath for his groũdes soche
playne truthes, & as I may say, suche vndowbtfull and sensible principles, And this
is the cause why all learned menne dooth approue the certenty of
geometry, and cõsequently of the other artes mathematical, which haue
the grounds (as Arithmeticke, musike and astronomy) aboue all other
artes and sciences, that be vsed amõgest men. Thus muche haue I sayd of
the first principles, and now will I go on with the theoremes, whiche I
do only by examples declare, minding to reserue the proofes to a peculiar
boke which I will then set forth, when I perceaue this to be thankfully
taken of the readers of it.
The theoremes of Geometry brieflye
declared by shorte examples.
The firste Theoreme.
When .ij. triangles be so drawen, that the one of thẽ hath ij. sides equal to ij sides of the [c.i.v] other triangle, and that the angles enclosed with those sides, bee equal also in bothe triangles, then is the thirde side likewise equall in them. And the whole triangles be of one greatnes, and euery angle in the one equall to his matche angle in the other, I meane those angles that be inclosed with like sides.
Example.
This triangle A.B.C. hath ij. sides (that is to say) C.A. and C.B, equal to ij. sides of the other triangle F.G.H, for A.C. is equall to F.G, and B.C. is equall to G.H. And also the angle C. contayned beetweene F.G, and G.H, for both of them answere to the eight parte of a circle. Therfore doth it remayne that A.B. whiche is the thirde lyne in the firste triangle, doth agre in lengthe with F.H, wch is the third line in ye secõd triãgle & ye hole triãgle. A.B.C. must nedes be equal to ye hole triangle F.G.H. And euery corner equall to his match, that is to say, A. equall to F, B. to H, and C. to G, for those bee called match corners, which are inclosed with like sides, other els do lye against like sides.
The second Theoreme.
In twileke triangles the ij. corners that be c.ij. about the groũd line, are equal togither. And if the sides that be equal, be drawẽ out in lẽgth thẽ wil the corners that are vnder the ground line, be equal also togither.
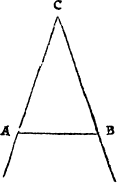
Example
A.B.C. is a twileke triangle, for the one side A.C, is equal to the other side B.C. And therfore I saye that the inner corners A. and B, which are about the ground lines, (that is A.B.) be equall togither. And farther if C.A. and C.B. bee drawen forthe vnto D. and E. as you se that I haue drawen them, then saye I that the two vtter angles vnder A. and B, are equal also togither: as the theorem said. The profe wherof, as of al the rest, shal apeare in Euclide, whome I intende to set foorth in english with sondry new additions, if I may perceaue that it wilbe thankfully taken.
The thirde Theoreme.
If in annye triangle there bee twoo angles equall togither, then shall the sides, that lie against those angles, be equal also.
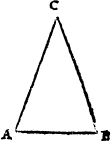
Example.
This triangle A.B.C. hath two corners equal eche to other, that is A. and B, as I do by supposition limite, wherfore it foloweth that the side A.C, is equal to that other side B.C, for the side A.C, lieth againste the angle B, and the side B.C, lieth against the angle A.
[c.ii.v]The fourth Theoreme.
When two lines are drawen frõ the endes of anie one line, and meet in anie pointe, it is not possible to draw two other lines of like lengthe ech to his match that shal begĩ at the same pointes, and end in anie other pointe then the twoo first did.
Example.
The first line is A.B, on which I haue erected two other lines A.C, and B.C, that meete in the pricke C, wherefore I say, it is not possible to draw ij. other lines from A. and B. which shal mete in one point (as you se A.D. and B.D. mete in D.) but that the match lines shalbe vnequal, I mean by match lines, the two lines on one side, that is the ij. on the right hand, or the ij. on the lefte hand, for as you se in this example A.D. is longer thẽ A.C, and B.C. is longer then B.D. And it is not possible, that A.C. and A.D. shall bee of one lengthe, if B.D. and B.C. bee like longe. For if one couple of matche lines be equall (as the same example A.E. is equall to A.C. in length) then must B.E. needes be vnequall to B.C. as you see, it is here shorter.
The fifte Theoreme.
If two triãgles haue there ij. sides equal one to an other, and their groũd lines equal also, then c.iij. shall their corners, whiche are contained betwene like sides, be equall one to the other.
Example.
Because these two triangles A.B.C, and D.E.F. haue two sides equall one to an other. For A.C. is equall to D.F, and B.C. is equall to E.F, and again their groũd lines A.B. and D.E. are lyke in length, therfore is eche angle of the one triangle equall to ech angle of the other, comparyng together those angles that are contained within lyke sides, so is A. equall to D, B. to E, and C. to F, for they are contayned within like sides, as before is said.
The sixt Theoreme.
When any right line standeth on an other, the ij. angles that thei make, other are both right angles, or els equall to .ij. righte angles.
Example.
A.B. is a right line, and on it there doth light another right line, drawen from C. perpendicularly on it, therefore saie I, that the .ij. angles that thei do make, are .ij. right angles as maie be iudged by the definition of a right angle. But in the second part of the example, where A.B. beyng still the right line, on which D. standeth [c.iii.v] in slope wayes, the two angles that be made of them are not righte angles, but yet they are equall to two righte angles, for so muche as the one is to greate, more then a righte angle, so muche iuste is the other to little, so that bothe togither are equall to two right angles, as you maye perceiue.
The seuenth Theoreme.
If .ij. lines be drawen to any one pricke in an other lyne, and those .ij. lines do make with the fyrst lyne, two right angles, other suche as be equall to two right angles, and that towarde one hande, than those two lines doo make one streyght lyne.
Example.
A.B. is a streyght lyne, on which there doth lyght two other lines one frome D, and the other frome C, but considerynge that they meete in one pricke E, and that the angles on one hand be equal to two right corners (as the laste theoreme dothe declare) therfore maye D.E. and E.C. be counted for one ryght lyne.
The eight Theoreme.
When two lines do cut one an other crosseways they do make their matche angles equall.
[c.iiii.]
Example.
What matche angles are, I haue tolde you in the definitions of the termes. And here A, and B. are matche corners in this example, as are also C. and D, so that the corner A, is equall to B, and the angle C, is equall to D.
The nynth Theoreme.
Whan so euer in any triangle the line of one side is drawen forthe in lengthe, that vtter angle is greater than any of the two inner corners, that ioyne not with it.
Example.
The triangle A.D.C hathe hys grounde lyne A.C. drawen forthe in lengthe vnto B, so that the vtter corner that it maketh at C, is greater then any of the two inner corners that lye againste it, and ioyne not wyth it, whyche are A. and D, for they both are lesser then a ryght angle, and be sharpe angles, but C. is a blonte angle, and therfore greater then a ryght angle.
The tenth Theoreme.
In euery triangle any .ij. corners, how so euer you take thẽ, ar lesse thẽ ij. right corners.
[c.iiii.v]Example.
In the firste triangle E, whiche is a threlyke, and therfore hath all his angles sharpe, take anie twoo corners that you will, and you shall perceiue that they be lesser then ij. right corners, for in euery triangle that hath all sharpe corners (as you see it to be in this example) euery corner is lesse then a right corner. And therfore also euery two corners must nedes be lesse then two right corners. Furthermore in that other triangle marked with M, whiche hath .ij. sharpe corners and one right, any .ij. of them also are lesse then two right angles. For though you take the right corner for one, yet the other whiche is a sharpe corner, is lesse then a right corner. And so it is true in all kindes of triangles, as you maie perceiue more plainly by the .xxij. Theoreme.
The .xi. Theoreme.
In euery triangle, the greattest side lieth against the greattest angle.
Example.
As in this triangle A.B.C, the greattest angle is C. And A.B. (whiche is the side that lieth against it) is the greatest and longest side. And contrary waies, as A.C. is the shortest side, so B. (whiche is the angle liyng against it) is the d.i. smallest and sharpest angle, for this doth folow also, that is the longest side lyeth against the greatest angle, so it that foloweth
The twelft Theoreme.
In euery triangle the greattest angle lieth against the longest side.
For these ij. theoremes are one in truthe.
The thirtenth theoreme.
In euerie triangle anie ij. sides togither how so euer you take them, are longer thẽ the thirde.
For example you shal take this triangle A.B.C. which hath a very blunt corner, and therfore one of his sides greater a good deale then any of the other, and yet the ij. lesser sides togither ar greater then it.* And if it bee so in a blunte angeled triangle, it must nedes be true in all other, for there is no other kinde of triangles that hathe the one side so greate aboue the other sids, as thei yt haue blunt corners.
The fourtenth theoreme.
If there be drawen from the endes of anie side of a triangle .ij. lines metinge within the triangle, those two lines shall be lesse then the other twoo sides of the triangle, but yet the [d.i.v] corner that thei make, shall bee greater then that corner of the triangle, whiche standeth ouer it.
Example.
A.B.C. is a triangle. on whose ground line A.B. there is drawen ij. lines, from the ij. endes of it, I say from A. and B, and they meete within the triangle in the pointe D, wherfore I say, that as those two lynes A.D. and B.D, are lesser then A.C. and B.C, so the angle D, is greatter then the angle C, which is the angle against it.
The fiftenth Theoreme.
If a triangle haue two sides equall to the two sides of an other triangle, but yet the ãgle that is contained betwene those sides, greater then the like angle in the other triangle, then is his grounde line greater then the grounde line of the other triangle.
Example.
A.B.C. is a triangle, whose sides A.C. and B.C, are equall to E.D. and D.F, the two sides of the triangle D.E.F, but bicause the angle in D, is greatter then the angle C. (whiche are the ij. angles contayned betwene the equal lynes) d.ij. therfore muste the ground line E.F. nedes bee greatter thenne the grounde line A.B, as you se plainely.
 |
 |
The xvi. Theoreme.
If a triangle haue twoo sides equalle to the two sides of an other triangle, but yet hathe a longer ground line thẽ that other triangle, then is his angle that lieth betwene the equall sides, greater thẽ the like corner in the other triangle.
Example.
This Theoreme is nothing els, but the sentence of the last Theoreme turned backward, and therfore nedeth none other profe nother declaration, then the other example.
The seuententh Theoreme.
If two triangles be such sort, that two angles of the one be equal to ij. angles of the other, and that one side of the one be equal to on side of the other, whether that side do adioyne to one of the equall corners, or els lye againste [d.ii.v] one of them, then shall the other twoo sides of those triangles bee equalle togither, and the thirde corner also shall be equall in those two triangles.
Example.
Bicause that A.B.C, the one triangle hath two corners A. and B, equal to D.E, that are twoo corners of the other triangle. D.E.F. and that they haue one side in theym bothe equall, that is A.B, which is equall to D.E, therefore shall both the other ij. sides be equall one to an other, as A.C. and B.C. equall to D.F. and E.F, and also the thirde angle in them both shal be equall, that is, the angle C. shal be equall to the angle F.
The eightenth Theoreme.
When on ij. right lines ther is drawen a third right line crosse waies, and maketh .ij. matche corners of the one line equall to the like twoo matche corners of the other line, then ar those two lines gemmow lines, or paralleles.
Example.
d.iij.
The .ij. fyrst lynes are A.B. and C.D, the thyrd lyne that crosseth them is E.F. And bycause that E.F. maketh ij. matche angles with A.B, equall to .ij. other lyke matche angles on C.D, (that is to say E.G, equall to K.F, and M.N. equall also to H.L.) therfore are those ij. lynes A.B. and C.D. gemow lynes, vnderstand here by lyke matche corners, those that go one way as doth E.G, and K.F, lyke ways N.M, and H.L, for as E.G. and H.L, other N.M. and K.F. go not one waie, so be not they lyke match corners.
The nyntenth Theoreme.
When on two right lines there is drawen a thirde right line crossewaies, and maketh the ij. ouer corners towarde one hande equall togither, then ar those .ij. lines paralleles. And in like maner if two inner corners toward one hande, be equall to .ii. right angles.
Example.
As the Theoreme dothe speake of .ij. ouer angles, so muste you vnderstande also of .ij. nether angles, for the iudgement is lyke in bothe. Take for example the figure of the last theoreme, where A.B, and C.D, be called paralleles also, bicause E. and K, (whiche are .ij. ouer corners) are equall, and lykewaies L. and M. And so are in lyke maner the nether corners N. and H, and G. and F. Nowe to the seconde parte of the theoreme, those .ij. lynes A.B. and C.D, shall be called paralleles, because the ij. inner corners. As for example those two that bee toward the right hande (that is G. and L.) are [d.iii.v] equall (by the fyrst parte of this nyntenth theoreme) therfore muste G. and L. be equall to two ryght angles.
The xx. Theoreme.
When a right line is drawen crosse ouer .ij. right gemow lines, it maketh .ij. matche corners of the one line, equall to two matche corners of the other line, and also bothe ouer corners of one hande equall togither, and bothe nether corners like waies, and more ouer two inner corners, and two vtter corners also towarde one hande, equall to two right angles.
Example.
Bycause A.B. and C.D, (in the laste figure) are paralleles, therefore the two matche corners of the one lyne, as E.G. be equall vnto the .ij. matche corners of the other line, that is K.F, and lykewaies M.N, equall to H.L. And also E. and K. bothe ouer corners of the lefte hande equall togyther, and so are M. and L, the two ouer corners on the ryghte hande, in lyke maner N. and H, the two nether corners on the lefte hande, equall eche to other, and G. and F. the two nether angles on the right hande equall togither.
¶ Farthermore yet G. and L. the .ij. inner angles on the right hande bee equall to two right angles, and so are M. and F. the .ij. vtter angles on the same hande, in lyke manner shall you say of N. and K. the two inner corners on the left hand. and of E. and H. the two vtter corners on the same hande. And thus you see the agreable sentence of these .iii. theoremes to tende to this purpose, to declare by the angles how to iudge paralleles, and contrary waies howe you may by paralleles iudge the proportion of the angles.
[d.iiii.]The xxi. Theoreme.
What so euer lines be paralleles to any other line, those same be paralleles togither.
Example.
![]()
A.B. is a gemow line, or a parallele vnto C.D. And E.F, lykewaies is a parallele vnto C.D. Wherfore it foloweth, that A.B. must nedes bee a parallele vnto E.F.
The .xxij. theoreme.
In euery triangle, when any side is drawen forth in length, the vtter angle is equall to the ij. inner angles that lie againste it. And all iij. inner angles of any triangle are equall to ij. right angles.
Example.
The triangle beeyng A.D.E. and the syde A.E. drawen foorthe vnto B, there is made an vtter corner, whiche is C, and this vtter corner C, is equall to bother the inner corners that lye agaynst it, whyche are A. and D. And all thre inner corners, that is to say, A.D. and E, are equall to two ryght corners, whereof it foloweth, that all the three corners of any one triangle are equall to all the three corners of euerye other triangle. For what so euer thynges are equalle to anny one thyrde thynge, those same are [d.iiii.v] equalle togitther, by the fyrste common sentence, so that bycause all the .iij. angles of euery triangle are equall to two ryghte angles, and all ryghte angles bee equall togyther (by the fourth request) therfore must it nedes folow, that all the thre corners of euery triangle (accomptyng them togyther) are equall to iij. corners of any triangle, taken all togyther.
The .xxiii. theoreme.
When any ij. right lines doth touche and couple .ij. other righte lines, whiche are equall in length and paralleles, and if those .ij. lines bee drawen towarde one hande, then are thei also equall together, and paralleles.
Example.

A.B. and C.D. are ij. ryght lynes and paralleles and equall in length, and they ar touched and ioyned togither by ij. other lynes A.C. and B.D, this beyng so, and A.C. and B.D. beyng drawen towarde one syde (that is to saye, bothe towarde the lefte hande) therefore are A.C. and B.D. bothe equall and also paralleles.
The .xxiiij. theoreme.
In any likeiamme the two contrary sides ar equall togither, and so are eche .ij. contrary angles, and the bias line that is drawen in it, dothe diuide it into two equall portions.
e.i.Example.
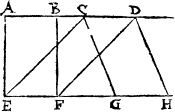
Here ar two likeiammes ioyned togither, the one is a longe square A.B.E, and the other is a losengelike D.C.E.F. which ij. likeiammes ar proued equall togither, bycause they haue one ground line, that is, F.E, And are made betwene one payre of gemow lines, I meane A.D. and E.H. By this Theoreme may you know the arte of the righte measuringe of likeiammes, as in my booke of measuring I wil more plainly declare.
There is no xxv. (25th) theorem.
The xxvi. Theoreme.
All likeiammes that haue equal grounde lines and are drawen betwene one paire of paralleles, are equal togither.
Example.
Fyrste you muste marke the difference betwene this Theoreme and the laste, for the laste Theoreme presupposed to the diuers likeiammes one ground line common to them, but this theoreme doth presuppose a diuers ground line for euery likeiamme, only meaning them to be equal in length, though they be diuers in numbre. As for example. In the last figure ther are two parallels, A.D. and E.H, and betwene them are drawen thre likeiammes, the firste is, A.B.E.F, the second is E.C.D.F, and the thirde is C.G.H.D. The firste and the seconde haue one ground line, (that is E.F.) and therfore in so muche as they are betwene one paire of paralleles, they are equall accordinge to the fiue and twentye Theoreme, but the thirde likeiamme that is C.G.H.D. hathe his grounde line G.H, seuerall frome [e.i.v] the other, but yet equall vnto it. wherefore the third likeiam is equall to the other two firste likeiammes. And for a proofe that G.H. being the groũd line of the third likeiamme, is equal to E.F, whiche is the ground line to both the other likeiams, that may be thus declared, G.H. is equall to C.D, seynge they are the contrary sides of one likeiamme (by the foure and twẽty theoreme) and so are C.D. and E.F. by the same theoreme. Therfore seynge both those ground lines E.F. and G.H, are equall to one thirde line (that is C.D.) they must nedes bee equall togyther by the firste common sentence.
The xxvii. Theoreme.
All triangles hauinge one grounde lyne, and standing betwene one paire of parallels, ar equall togither.
Example.
A.B. and C.F. are twoo gemowe lines, betweene which there be made two triangles, A.D.E. and D.E.B, so that D.E, is the common ground line to them bothe. wherfore it doth folow, that those two triangles A.D.E. and D.E.B. are equall eche to other.
The xxviij. Theoreme.
All triangles that haue like long ground lines, and bee made betweene one paire of gemow lines, are equall togither.
e.ijExample.
Example of this Theoreme you may see in the last figure, where as sixe triangles made betwene those two gemowe lines A.B. and C.F, the first triangle is A.C.D, the seconde is A.D.E, the thirde is A.D.B, the fourth is A.B.E, the fifte is D.E.B, and the sixte is B.E.F, of which sixe triangles, A.D.E. and D.E.B. are equall, bicause they haue one common grounde line. And so likewise A.B.E. and A.B.D, whose commen grounde line is A.B, but A.C.D. is equal to B.E.F, being both betwene one couple of parallels, not bicause thei haue one ground line, but bicause they haue their ground lines equall, for C.D. is equall to E.F, as you may declare thus. C.D, is equall to A.B. (by the foure and twenty Theoreme) for thei are two contrary sides of one lykeiamme. A.C.D.B, and E.F by the same theoreme, is equall to A.B, for thei ar the two ye contrary sides of the likeiamme, A.E.F.B, wherfore C.D. must needes be equall to E.F. like wise the triangle A.C.D, is equal to A.B.E, bicause they ar made betwene one paire of parallels and haue their groundlines like, I meane C.D. and A.B. Againe A.D.E, is equal to eche of them both, for his ground line D.E, is equall to A.B, inso muche as they are the contrary sides of one likeiamme, that is the long square A.B.D.E. And thus may you proue the equalnes of all the reste.
The xxix. Theoreme.
Al equal triangles that are made on one grounde line, and rise one waye, must needes be betwene one paire of parallels.
Example.
Take for example A.D.E, and D.E.B, which (as the xxvij. [e.ii.v] conclusion dooth proue) are equall togither, and as you see, they haue one ground line D.E. And againe they rise towarde one side, that is to say, vpwarde toward the line A.B, wherfore they must needes be inclosed betweene one paire of parallels, which are heere in this example A.B. and D.E.
The thirty Theoreme.
Equal triangles that haue their ground lines equal, and be drawẽ toward one side, ar made betwene one paire of paralleles.
Example.
The example that declared the last theoreme, maye well serue to the declaracion of this also. For those ij. theoremes do diffre but in this one pointe, that the laste theoreme meaneth of triangles, that haue one ground line common to them both, and this theoreme dothe presuppose the grounde lines to bee diuers, but yet of one length, as A.C.D, and B.E.F, as they are ij. equall triangles approued, by the eighte and twentye Theorem, so in the same Theorem it is declared, yt their groũd lines are equall togither, that is C.D, and E.F, now this beeynge true, and considering that they are made towarde one side, it foloweth, that they are made betwene one paire of parallels when I saye, drawen towarde one side, I meane that the triangles must be drawen other both vpward frome one parallel, other els both downward, for if the one be drawen vpward and the other downward, then are they drawen betwene two paire of parallels, presupposinge one to bee drawen by their ground line, and then do they ryse toward contrary sides.
[e.iii.]The xxxi. theoreme.
If a likeiamme haue one ground line with a triangle, and be drawen betwene one paire of paralleles, then shall the likeiamme be double to the triangle.
Example.
A.H. and B.G. are .ij. gemow lines, betwene which there is made a triangle B.C.G, and a lykeiamme, A.B.G.C, whiche haue a grounde lyne, that is to saye, B.G. Therfore doth it folow that the lyke iamme A.B.G.C. is double to the triangle B.C.G. For euery halfe of that lykeiamme is equall to the triangle, I meane A.B.F.E. other F.E.C.G. as you may coniecture by the .xi. conclusion geometrical.
And as this Theoreme dothe speake of a triangle and likeiamme that haue one groundelyne, so is it true also, yf theyr groundelynes bee equall, though they bee dyuers, so that thei be made betwene one payre of paralleles. And hereof may you perceaue the reason, why in measuryng the platte of a triangle, you must multiply the perpendicular lyne by halfe the grounde lyne, or els the hole grounde lyne by halfe the perpendicular, for by any of these bothe waies is there made a lykeiamme equall to halfe suche a one as shulde be made on the same hole grounde lyne with the triangle, and betweene one payre of paralleles. Therfore as that lykeiamme is double to the triangle, so the halfe of it, must needes be equall to the triangle. Compare the .xi. conclusion with this theoreme.
The .xxxij. Theoreme.
In all likeiammes where there are more than [e.iii.v] one made aboute one bias line, the fill squares of euery of them must nedes be equall.
Example.
Fyrst before I declare the examples, it shal be mete to shew the true vnderstãdyng of this theorem. Bias lyne. Therfore by the Bias line, I meane that lyne, whiche in any square figure dooth runne from corner to corner. And euery square which is diuided by that bias line into equall halues from corner to corner (that is to say, into .ij. equall triangles) those be counted to stande aboute one bias line, and the other squares, whiche touche that bias line, with one of their corners onely, those doo I call Fyll squares, Fyll squares. accordyng to the greke name, which is anapleromata, ἀναπληρώματα and called in latin supplementa, bycause that they make one generall square, includyng and enclosyng the other diuers squares, as in this exãple H.C.E.N. is one square likeiamme, and L.M.G.C. is an other, whiche bothe are made aboute one bias line, that is N.M, than K.L.H.C. and C.E.F.G. are .ij. fyll squares, for they doo fyll vp the sydes of the .ij. fyrste square lykeiammes, in suche sorte, that all them foure is made one greate generall square K.M.F.N.
Nowe to the sentence of the theoreme, I say, that the .ij. fill squares, H.K.L.C. and C.E.F.G. are both equall togither, (as it shall bee declared in the booke of proofes) bicause they are the fill squares of two likeiammes made aboute one bias line, as the exaumple sheweth. Conferre the twelfthe conclusion with this theoreme.
[e.iiii.]The xxxiij. Theoreme.
In all right anguled triangles, the square of that side whiche lieth against the right angle, is equall to the .ij. squares of both the other sides.
Example.
A.B.C. is a triangle, hauing a ryght angle in B. Wherfore it foloweth, that the square of A.C, (whiche is the side that lyeth agaynst the right angle) shall be as muche as the two squares of A.B. and B.C. which are the other .ij. sides.
¶ By the square of any lyne, you muste vnderstande a figure made iuste square, hauyng all his iiij. sydes equall to that line, whereof it is the square, so is A.C.F, the square of A.C. Lykewais A.B.D. is the square of A.B. And B.C.E. is the square of B.C. Now by the numbre of the diuisions in eche of these squares, may you perceaue not onely what the square of any line is called, but also that the theoreme is true, and expressed playnly bothe by lines and numbre. For as you see, the greatter square (that is A.C.F.) hath fiue diuisions on eche syde, all equall togyther, and those in the whole square are twenty and fiue. Nowe in the left square, whiche is A.B.D. there are but .iij. of those diuisions in one syde, and that yeldeth nyne in the whole. So lykeways you see in the meane square A.C.E. in euery syde .iiij. partes, whiche in the whole amount vnto sixtene. Nowe adde togyther all the partes of the two lesser squares, that is to saye, sixtene and nyne, and you perceyue that they make twenty and fiue, whyche is an equall numbre to the summe of the greatter square.
[e.iiii.v]By this theoreme you may vnderstand a redy way to know the syde of any ryght anguled triangle that is vnknowen, so that you knowe the lengthe of any two sydes of it. For by tournynge the two sydes certayne into theyr squares, and so addynge them togyther, other subtractynge the one from the other (accordyng as in the vse of these theoremes I haue sette foorthe) and then fyndynge the roote of the square that remayneth, which roote (I meane the syde of the square) is the iuste length of the vnknowen syde, whyche is sought for. But this appertaineth to the thyrde booke, and therefore I wyll speake no more of it at this tyme.
The xxxiiij. Theoreme.
If so be it, that in any triangle, the square of the one syde be equall to the .ij. squares of the other .ij. sides, than must nedes that corner be a right corner, which is conteined betwene those two lesser sydes.
Example.
As in the figure of the laste Theoreme, bicause A.C, made in square, is asmuch as the square of A.B, and also as the square of B.C. ioyned bothe togyther, therefore the angle that is inclosed betwene those .ij. lesser lynes, A.B. and B.C. (that is to say) the angle B. whiche lieth against the line A.C, must nedes be a ryght angle. This theoreme dothe so depende of the truthe of the laste, that whan you perceaue the truthe of the one, you can not iustly doubt of the others truthe, for they conteine one sentence, contrary waies pronounced.
The .xxxv. theoreme.
If there be set forth .ij. right lines, and one of them parted into sundry partes, how many f.i. or few so euer they be, the square that is made of those ij. right lines proposed, is equal to all the squares, that are made of the vndiuided line, and euery parte of the diuided line.
Example.
The ij. lines proposed ar A.B. and C.D, and the lyne A.B. is deuided into thre partes by E. and F. Now saith this theoreme, that the square that is made of those two whole lines A.B. and C.D, so that the line A.B. stãdeth for the lẽgth of the square, and the other line C.D. for the bredth of the same. That square (I say) wil be equall to all the squares that be made, of the vndiueded lyne (which is C.D.) and euery portion of the diuided line. And to declare that particularly, Fyrst I make an other line G.K, equall to the line .C.D, and the line G.H. to be equal to the line A.B, and to bee diuided into iij. like partes, so that G.M. is equall to A.E, and M.N. equal to E.F, and then muste N.H. nedes remaine equall to F.B. Then of those ij. lines G.K, vndeuided, and G.H. which is deuided, I make a square, that is G.H.K.L, In which square if I drawe crosse lines frome one side to the other, according to the diuisions of the line G.H, then will it appear plaine, that the theoreme doth affirme. For the first square G.M.O.K, must needes be equal to the square of the line C.D, and the first portiõ of the diuided line, which is A.E, for bicause their sides are equall. And so the seconde [f.i.v] square that is M.N.P.O, shall be equall to the square of C.D, and the second part of A.B, that is E.F. Also the third square which is N.H.L.P, must of necessitee be equal to the square of C.D, and F.B, bicause those lines be so coupeled that euery couple are equall in the seuerall figures. And so shal you not only in this example, but in all other finde it true, that if one line be deuided into sondry partes, and an other line whole and vndeuided, matched with him in a square, that square which is made of these two whole lines, is as muche iuste and equally, as all the seuerall squares, whiche bee made of the whole line vndiuided, and euery part seuerally of the diuided line.
The xxxvi. Theoreme.
If a right line be parted into ij. partes, as chaunce may happe, the square that is made of the whole line, is equall to bothe the squares that are made of the same line, and the twoo partes of it seuerally.
Example.
The line propounded beyng A.B. and deuided, as chaunce happeneth, in C. into ij. vnequall partes, I say that the square made of the hole line A.B, is equal to the two squares made of the same line with the twoo partes of itselfe, as with A.C, and with C.B, for the square D.E.F.G. is equal to the two other partial squares of D.H.K.G and H.E.F.K, but that the greater square is equall to the square of the whole line A.B, and the f.ii. partiall squares equall to the squares of the second partes of the same line ioyned with the whole line, your eye may iudg without muche declaracion, so that I shall not neede to make more exposition therof, but that you may examine it, as you did in the laste Theoreme.
The xxxvij. Theoreme.
If a right line be deuided by chaunce, as it maye happen, the square that is made of the whole line, and one of the partes of it which soeuer it be, shal be equall to that square that is made of the ij. partes ioyned togither, and to an other square made of that part, which was before ioyned with the whole line.
Example.
The line A.B. is deuided in C. into twoo partes, though not equally, of which two partes for an example I take the first, that is A.C, and of it I make one side of a square, as for example D.G. accomptinge those two lines to be equall, the other side of the square is D.E, whiche is equall to the whole line A.B.
Now may it appeare, to your eye, that the great square made of the whole line A.B, and of one of his partes that is A.C, [f.ii.v] (which is equall with D.G.) is equal to two partiall squares, whereof the one is made of the saide greatter portion A.C, in as muche as not only D.G, beynge one of his sides, but also D.H. beinge the other side, are eche of them equall to A.C. The second square is H.E.F.K, in which the one side H.E, is equal to C.B, being the lesser parte of the line, A.B, and E.F. is equall to A.C. which is the greater parte of the same line. So that those two squares D.H.K.G and H.E.F.K, bee bothe of them no more then the greate square D.E.F.G, accordinge to the wordes of the Theoreme afore saide.
The xxxviij. Theoreme.
If a righte line be deuided by chaunce, into partes, the square that is made of that whole line, is equall to both the squares that ar made of eche parte of the line, and moreouer to two squares made of the one portion of the diuided line ioyned with the other in square.
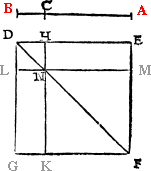
Example.
The labels A and B were transposed in the illustration as an alternative to transposing all occurrences of A.C and C.B in the text.
Lette the diuided line bee A.B, and parted in C, into twoo partes: Nowe saithe the Theoreme, that the square of the whole lyne A.B, is as mouche iuste as the square of A.C, and the square of C.B, eche by it selfe, and more ouer by as muche twise, as A.C. and C.B. f iii ioyned in one square will make. For as you se, the great square D.E.F.G, conteyneth in hym foure lesser squares, of whiche the first and the greatest is N.M.F.K, and is equall to the square of the lyne A.C. The second square is the lest of them all, that is D.H.L.N, and it is equall to the square of the line C.B. Then are there two other longe squares both of one bygnes, that is H.E.N.M. and L.N.G.K, eche of them both hauyng .ij. sides equall to A.C, the longer parte of the diuided line, and there other two sides equall to C.B, beeyng he shorter parte of the said line A.B.
So is that greatest square, beeyng made of the hole lyne A.B, equal to the ij. squares of eche of his partes seuerally, and more by as muche iust as .ij. longe squares, made of the longer portion of the diuided lyne ioyned in square with the shorter parte of the same diuided line, as the theoreme wold. And as here I haue put an example of a lyne diuided into .ij. partes, so the theoreme is true of all diuided lines, of what number so euer the partes be, foure, fyue, or syxe. etc.
This theoreme hath great vse, not only in geometrie, but also in arithmetike, as herafter I will declare in conuenient place.
The .xxxix. theoreme.
If a right line be deuided into two equall partes, and one of these .ij. partes diuided agayn into two other partes, as happeneth the longe square that is made of the thyrd or later part of that diuided line, with the residue of the same line, and the square of the mydlemoste parte, are bothe togither equall to the square of halfe the firste line.
[f.iii.v]Example.
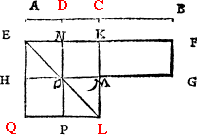
The line A.B. is diuided into ij. equal partes in C, and that parte C.B. is diuided agayne as hapneth in D. Wherfore saith the Theorem that the long square made of D.B. and A.D, with the square of C.D. (which is the mydle portion) shall bothe be equall to the square of half the lyne A.B, that is to saye, to the square of A.C, or els of C.D, which make all one. The long square F.G.N.O. whiche is the longe square that the theoreme speaketh of, is made of .ij. long squares, wherof the fyrst is F.G.M.K, and the seconde is K.N.O.M. The square of the myddle portion is L.M.O.P. and the square of the halfe of the fyrste lyne is E.K.Q.L. Nowe by the theoreme, that longe square F.G.N.O, with the iuste square L.M.O.P, muste bee equall to the greate square E.K.Q.L, whyche thynge bycause it seemeth somewhat difficult to vnderstande, althoughe I intende not here to make demonstrations of the Theoremes, bycause it is appoynted to be done in the newe edition of Euclide, yet I wyll shew you brefely how the equalitee of the partes doth stande. And fyrst I say, that where the comparyson of equalitee is made betweene the greate square (whiche is made of halfe the line A.B.) and two other, where of the fyrst is the longe square F.G.N.O, and the second is the full square L.M.O.P, which is one portion of the great square all redye, and so is that longe square K.N.M.O, beynge a parcell also of the longe square F.G.N.O, Wherfore as those two partes are common to bothe partes compared in equalitee, and therfore beynge bothe abated from eche parte, if the reste of bothe the other partes bee equall, than were those whole partes equall before: Nowe the reste of the great square, those [f.iiii.] two lesser squares beyng taken away, is that longe square E.N.P.Q, whyche is equall to the long square F.G.K.M, beyng the rest of the other parte. And that they two be equall, theyr sydes doo declare. For the longest lynes that is F.K and E.Q are equall, and so are the shorter lynes, F.G, and E.N, and so appereth the truthe of the Theoreme.
The .xl. theoreme.
If a right line be diuided into .ij. euen partes, and an other right line annexed to one ende of that line, so that it make one righte line with the firste. The longe square that is made of this whole line so augmented, and the portion that is added, with the square of halfe the right line, shall be equall to the square of that line, whiche is compounded of halfe the firste line, and the parte newly added.
Example.
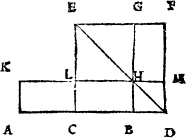
The fyrst lyne propounded is A.B, and it is diuided into ij. equall partes in C, and an other ryght lyne, I meane B.D annexed to one ende of the fyrste lyne.
Nowe say I, that the long square A.D.M.K, is made of the whole lyne so augmẽted, that is A.D, and the portiõ annexed, yt is D.M, for D.M is equall to B.D, wherfore yt long square A.D.M.K, with the [f.iiii.v] square of halfe the first line, that is E.G.H.L, is equall to the great square E.F.D.C. whiche square is made of the line C.D. that is to saie, of a line compounded of halfe the first line, beyng C.B, and the portion annexed, that is B.D. And it is easyly perceaued, if you consyder that the longe square A.C.L.K. (whiche onely is lefte out of the great square) hath another longe square equall to hym, and to supply his steede in the great square, and that is G.F.M.H. For their sydes be of lyke lines in length.
The xli. Theoreme.
If a right line bee diuided by chaunce, the square of the same whole line, and the square of one of his partes are iuste equall to the lõg square of the whole line, and the sayde parte twise taken, and more ouer to the square of the other parte of the sayd line.
Example.
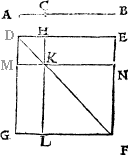
A.B. is the line diuided in C. And D.E.F.G, is the square of the whole line, D.H.K.M. is the square of the lesser portion (whyche I take for an example) and therfore must bee twise reckened. Nowe I saye that those ij. squares are equall to two longe squares of the whole line A.B, and his sayd portion A.C, and also to the square of the other portion of the sayd first line, whiche portion is C.B, and his square K.N.F.L. In this theoreme there is no difficultie, if you cõsyder that the litle square D.H.K.M. is .iiij. tymes reckened, that is to say, fyrst of all as a parte of the greatest square, whiche is D.E.F.G. Secondly he is rekned g.i. by him selfe. Thirdely he is accompted as parcell of the long square D.E.N.M, And fourthly he is taken as a part of the other long square D.H.L.G, so that in as muche as he is twise reckened in one part of the comparisõ of equalitee, and twise also in the second parte, there can rise none occasion of errour or doubtfulnes therby.
The xlij. Theoreme.
If a right line be deuided as chance happeneth the iiij. long squares, that may be made of that whole line and one of his partes with the square of the other part, shall be equall to the square that is made of the whole line and the saide first portion ioyned to him in lengthe as one whole line.
Example.
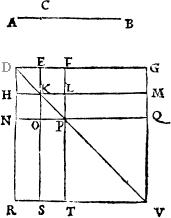
The firste line is A.B, and is deuided by C. into two vnequall partes as happeneth. The long square of yt, and his lesser portion A.C, is foure times drawen, the first is E.G.M.K, the seconde is K.M.Q.O, the third is H.K.R.S, and the fourthe is K.L.S.T. And where as it appeareth that one of the little squares (I meane K.L.P.O) is reckened twise, ones as parcell of the second long square and agayne as parte of the [g.i.v] thirde long square, to auoide ambiguite, you may place one insteede of it, an other square of equalitee, with it. that is to saye, D.E.K.H, which was at no tyme accompting as parcell of any one of them, and then haue you iiij. long squares distinctly made of the whole line A.B, and his lesser portion A.C. And within them is there a greate full square P.Q.T.V. whiche is the iust square of B.C, beynge the greatter portion of the line A.B. And that those fiue squares doo make iuste as muche as the whole square of that longer line D.G, (whiche is as longe as A.B, and A.C. ioyned togither) it may be iudged easyly by the eye, sith that one greate square doth comprehẽd in it all the other fiue squares, that is to say, foure long squares (as is before mencioned) and one full square. which is the intent of the Theoreme.
The xliij. Theoreme.
If a right line be deuided into ij. equal partes first, and one of those parts again into other ij. parts, as chaũce hapeneth, the square that is made of the last part of the line so diuided, and the square of the residue of that whole line, are double to the square of halfe that line, and to the square of the middle portion of the same line.
Example.
The line to be deuided is A.B, and is parted in C. into two equall partes, and then C.B, is deuided againe into two partes in D, so that the meaninge of the Theoreme, is that the g.ij. square of D.B. which is the latter parte of the line, and the square of A.D, which is the residue of the whole line. Those two squares, I say, ar double to the square of one halfe of the line, and to the square of C.D, which is the middle portion of those thre diuisions. Which thing that you maye more easilye perceaue, I haue drawen foure squares, whereof the greatest being marked with E. is the square of A.D. The next, which is marked with G, is the square of halfe the line, that is, of A.C, And the other two little squares marked with F. and H, be both of one bignes, by reason that I did diuide C.B. into two equall partes, so that you amy take the square F, for the square of D.B, and the square H, for the square of C.D. Now I thinke you doubt not, but that the square E. and the square F, ar double so much as the square G. and the square H, which thing the easyer is to be vnderstande, bicause that the greate square hath in his side iij. quarters of the firste line, which multiplied by itselfe maketh nyne quarters, and the square F. containeth but one quarter, so that bothe doo make tenne quarters.
Then G. contayneth iiij. quarters, seynge his side
containeth
twoo, and H. containeth but one quarter, whiche both make
but fiue quarters, and that is but halfe of tenne.
Whereby you may easylye coniecture,
that the meanynge of the the-
oreme is verified in the
figures of this ex-
ample.
The xliiij. Theoreme.
If a right line be deuided into ij. partes equally, and an other portion of a righte lyne annexed to that firste line, the square of this whole line so compounded, and the square of the portion that is annexed, ar doule as much as the square of the halfe of the firste line, and the square of the other halfe ioyned in one with the annexed portion, as one whole line.
Example.
The line is A.B, and is diuided firste into twoo equal partes in C, and thẽ is there annexed to it an other portion whiche is B.D. Now saith the Theoreme, that the square of A.D, and the square of B.D, ar double to the square of A.C, and to the square of C.D. The line A.B. cõtaining four partes, then must needes his halfe containe ij. partes of such partes I suppose B.D. (which is the ãnexed line) to containe thre, so shal the hole line cõprehend vij. parts, and his square xlix. parts, where vnto if you ad ye square g.iij. of the annexed lyne, whiche maketh nyne, than those bothe doo yelde, lviij. whyche must be double to the square of the halfe lyne with the annexed portion. The halfe lyne by it selfe conteyneth but .ij. partes, and therfore his square dooth make foure. The halfe lyne with the annexed portion conteyneth fiue, and the square of it is .xxv, now put foure to .xxv, and it maketh iust .xxix, the euen halfe of fifty and eight, wherby appereth the truthe of the theoreme.
The .xlv. theoreme.
In all triangles that haue a blunt angle, the square of the side that lieth against the blunt angle, is greater than the two squares of the other twoo sydes, by twise as muche as is comprehended of the one of those .ij. sides (inclosyng the blunt corner) and the portion of the same line, beyng drawen foorth in lengthe, which lieth betwene the said blunt corner and a perpendicular line lightyng on it, and drawen from one of the sharpe angles of the foresayd triangle.
Example.
For the declaration of this theoreme and the next also, whose vse are wonderfull in the practise of Geometrie, and in measuryng especially, it shall be nedefull to declare that euery triangle that hath no ryght angle as those whyche are called (as in the boke of practise is declared) sharp cornered triangles, and blunt cornered triangles, yet may they be brought to haue a ryght angle, eyther by partyng them into two lesser triangles, [g.iii.v] or els by addyng an other triangle vnto them, whiche may be a great helpe for the ayde of measuryng, as more largely shall be sette foorthe in the boke of measuryng. But for this present place, this forme wyll I vse, (whiche Theon also vseth) to adde one triangle vnto an other, to bryng the blunt cornered triangle into a ryght angled triangle, whereby the proportion of the squares of the sides in suche a blunt cornered triangle may the better bee knowen.
Fyrst therfore I sette foorth the triangle A.B.C, whose corner by C. is a blunt corner as you maye well iudge, than to make an other triangle of yt with a ryght angle, I must drawe forth the side B.C. vnto D, and frõ the sharp corner by A. I brynge a plumbe lyne or perpẽdicular on D. And so is there nowe a newe triangle A.B.D. whose angle by D. is a right angle. Nowe accordyng to the meanyng of the Theoreme, I saie, that in the first triangle A.B.C, because it hath a blunt corner at C, the square of the line A.B. whiche lieth against the said blunte corner, is more [g.iiii.] then the square of the line A.C, and also of the lyne B.C, (whiche inclose the blunte corner) by as muche as will amount twise of the line B.C, and that portion D.C. whiche lieth betwene the blunt angle by C, and the perpendicular line A.D.
The square of the line A.B, is the great square marked with E. The square of A.C, is the meane square marked with F. The square of B.C, is the least square marked with G. And the long square marked with K, is sette in steede of two squares made of B.C, and C.D. For as the shorter side is the iuste lengthe of C.D, so the other longer side is iust twise so longe as B.C, Wherfore I saie now accordyng to the Theoreme, that the greatte square E, is more then the other two squares F. and G, by the quantitee of the longe square K, wherof I reserue the profe to a more conuenient place, where I will also teache the reason howe to fynde the lengthe of all suche perpendicular lynes, and also of the line that is drawen betweene the blunte angle and the perpendicular line, with sundrie other very pleasant conclusions.
Labeling of rectangle K is conjectural. Other configurations of B, C and D will also fit, but the printed illustration (B and D on the right, nothing on the left) will not. The text requires a rectangle with BC as one side and CD as the other, doubled as in the next illustration (H.K).
The .xlvi. Theoreme.
In sharpe cornered triangles, the square of anie side that lieth against a sharpe corner, is lesser then the two squares of the other two sides, by as muche as is comprised twise in the long square of that side, on whiche the perpendicular line falleth, and the portion of that same line, liyng betweene the perpendicular, and the foresaid sharpe corner.
Example.
[g.iiii.v]
Fyrst I sette foorth the triangle A.B.C, and in yt I draw a plũbe line from the angle C. vnto the line A.B, and it lighteth in D. Nowe by the theoreme the square of B.C. is not so muche as the square of the other two sydes, that of B.A. and of A.C. by as muche as is twise conteyned in the lõg square made of A.B, and A.D, A.B. beyng the line or syde on which the perpendicular line falleth, and A.D. beeyng that portion of the same line whiche doth lye betwene the perpendicular line, and the sayd sharpe angle limitted, whiche angle is by A.
For declaration of the figures, the square marked with E. is the square of B.C, whiche is the syde that lieth agaynst the sharpe angle, the square marked with G. is the square of A.B, and the square marked with F. is the square of A.C, and the two longe squares marked with H.K, are made of the hole line A.B, and one of his portions A.D. And truthe it is that the square E. is lesser than the other two squares C. and F. by the quantitee of those two long squares H. and K. Wherby you may consyder agayn, an other proportion of equalitee, h.i. that is to saye, that the square E. with the twoo longsquares H.K, are iuste equall to the other twoo squares C. and F. And so maye you make, as it were an other theoreme. That in al sharpe cornered triangles, where a perpendicular line is drawen frome one angle to the side that lyeth againste it, the square of anye one side, with the ij. longesquares made at that hole line, whereon the perpendicular line doth lighte, and of that portion of it, which ioyneth to that side whose square is all ready taken, those thre figures, I say, are equall to the ij. squares, of the other ij. sides of the triangle. In whiche you muste vnderstand, that the side on which the perpendiculare falleth, is thrise vsed, yet is his square but ones mencioned, for twise he is taken for one side of the two long squares. And as I haue thus made as it were an other theoreme out of this fourty and sixe theoreme, so mighte I out of it, and the other that goeth nexte before, make as manny as woulde suffice for a whole booke, so that when they shall bee applyed to practise, and consequently to expresse their benefite, no manne that hathe not well wayde their wonderfull commoditee, would credite the possibilitie of their wonderfull vse, and large ayde in knowledge. But all this wyll I remitte to a place conuenient.
The xlvij. Theoreme.
If ij. points be marked in the circumferẽce of a circle, and a right line drawen frome the one to the other, that line must needes fal within the circle.
Example.
The circle is A.B.C.D, the ij. poinctes are A.B, the righte [h.i.v] line that is drawenne frome the one to the other, is the line A.B, which as you see, must needes lyghte within the circle. So if you putte the pointes to be A.D, or D.C, or A.C, other B.C, or B.D, in any of these cases you see, that the line that is drawen from the one pricke to the other dothe euermore run within the edge of the circle, els canne it be no right line. How be it, that a croked line, especially being more croked then the portion of the circumference, maye bee drawen from pointe to pointe withoute the circle. But the theoreme speaketh only of right lines, and not of croked lines.
The xlviij. Theoreme.
If a righte line passinge by the centre of a circle, doo crosse an other right line within the same circle, passinge beside the centre, if he deuide the saide line into twoo equal partes, then doo they make all their angles righte. And contrarie waies, if they make all their angles righte, then doth the longer line cutte the shorter in twoo partes.
Example.
The circle is A.B.C.D, the line that passeth by the centre, is A.E.C, the line that goeth beside the centre is D.B. Nowe h.ij. saye I, that the line A.E.C, dothe cutte that other line D.B. into twoo iuste partes, and therefore all their four angles ar righte angles. And contrarye wayes, bicause all their angles are righte angles, therfore it muste be true, that the greater cutteth the lesser into two equal partes, accordinge as the Theoreme would.
The xlix. Theoreme.
If twoo right lines drawen in a circle doo crosse one an other, and doo not passe by the centre, euery of them dothe not deuide the other into equall partions.
Example.
The circle is A.B.C.D, and the centre is E, the one line A.C, and the other is B.D, which two lines crosse one an other, but yet they go not by the centre, wherefore accordinge to the woordes of the theoreme, eche of theim doth cuytte the other into equall portions. For as you may easily iudge, A.C. hath one portiõ lõger and an other shorter, and so like wise B.D. Howbeit, it is not so to be vnderstãd, but one of them may be deuided into ij. euẽ parts, [h.ii.v] but bothe to bee cutte equally in the middle, is not possible, onles both passe through the cẽtre, therfore much rather whẽ bothe go beside the centre, it can not be that eche of theym shoulde be iustely parted into ij. euen partes.
The L. Theoreme.
If two circles crosse and cut one an other, then haue not they both one centre.
Example.
This theoreme seemeth of it selfe so manifest, that it neadeth nother demonstration nother declaraciõ. Yet for the plaine vnderstanding of it, I haue sette forthe a figure here, where ij. circles be drawẽ, so that one of them doth crosse the other (as you see) in the pointes B. and G, and their centres appear at the firste sighte to bee diuers. For the centre of the one is F, and the centre of the other is E, which diffre as farre asondre as the edges of the circles, where they bee most distaunte in sonder.
The Li. Theoreme.
If two circles be so drawen, that one of them do touche the other, then haue they not one centre.
h.iij.
Example.
There are two circles made, as you see, the one is A.B.C, and hath his centre by G, the other is B.D.E, and his centre is by F, so that it is easy enough to perceaue that their centres doe dyffer as muche a sonder, as the halfe diameter of the greater circle is lõger then the half diameter of the lesser circle. And so must it needes be thought and said of all other circles in lyke kinde.
The .lij. theoreme.
If a certaine pointe be assigned in the diameter of a circle, distant from the centre of the said circle, and from that pointe diuerse lynes drawen to the edge and circumference of the same circle, the longest line is that whiche passeth by the centre, and the shortest is the residew of the same line. And of al the other lines that is euer the greatest, that is nighest to the line, which passeth by the centre. And cõtrary waies, that is the shortest, that is farthest from it. And amongest thẽ all there can be but onely .ij. equall together, and they must nedes be so placed, that the shortest line shall be in the iust middle betwixte them.
[h.iii.v]Example.
The circle is A.B.C.D.E.H, and his centre is F, the diameter is A.E, in whiche diameter I haue taken a certain point distaunt from the centre, and that pointe is G, from which I haue drawen .iiij. lines to the circumference, beside the two partes of the diameter, whiche maketh vp vi. lynes in all. Nowe for the diuersitee in quantitie of these lynes, I saie accordyng to the Theoreme, that the line whiche goeth by the centre is the longest line, that is to saie, A.G, and the residewe of the same diameter beeyng G.E, is the shortest lyne. And of all the other that lyne is longest, that is neerest vnto that parte of the diameter whiche gooeth by the centre, and that is shortest, that is farthest distant from it, wherefore I saie, that G.B, is longer then G.C, and therfore muche more longer then G.D, sith G.C, also is longer then G.D, and by this maie you soone perceiue, that it is not possible to drawe .ij. lynes on any one side of the diameter, whiche might be equall in lengthe together, but on the one side of the diameter maie you easylie make one lyne equall to an other, on the other side of the same diameter, as you see in this example G.H, to bee equall to G.D, betweene whiche the lyne G.E, (as the shortest in all the circle) doothe stande euen distaunte from eche of them, and it is the precise knoweledge of their equalitee, if they be equally distaunt from one halfe of the diameter. Where as contrary waies if the one be neerer to any one halfe of the diameter then the other is, it is not possible that they two may be equall in lengthe, namely if they dooe ende bothe in the circumference of the [h.iiii.] circle, and be bothe drawen from one poynte in the diameter, so that the saide poynte be (as the Theoreme doeth suppose) somewhat distaunt from the centre of the said circle. For if they be drawen from the centre, then must they of necessitee be all equall, howe many so euer they bee, as the definition of a circle dooeth importe, withoute any regarde how neere so euer they be to the diameter, or how distante from it. And here is to be noted, that in this Theoreme, by neerenesse and distaunce is vnderstand the nereness and distaunce of the extreeme partes of those lynes where they touche the circumference. For at the other end they do all meete and touche.
The .liij. Theoreme.
If a pointe bee marked without a circle, and from it diuerse lines drawen crosse the circle, to the circumference on the other side, so that one of them passe by the centre, then that line whiche passeth by the centre shall be the loongest of them all that crosse the circle. And of the other lines those are longest, that be nexte vnto it that passeth by the centre. And those ar shortest, that be farthest distant from it. But among those partes of those lines, whiche ende in the outewarde circumference, that is most shortest, whiche is parte of the line that passeth by the centre, and amongeste the [h.iiii.v] othere eche, of thẽ, the nerer they are vnto it, the shorter they are, and the farther from it, the longer they be. And amongest them all there can not be more then .ij. of any one lẽgth, and they two muste be on the two contrarie sides of the shortest line.
Example.
Take the circle to be A.B.C, and the point assigned without it to be D. Now say I, that if there be drawen sundrie lines from D, and crosse the circle, endyng in the circumference on the cõtrary side, as here you see, D.A, D.E, D.F, and D.B, then of all these lines the longest must needes be D.A, which goeth by the centre of the circle, and the nexte vnto it, that is D.E, is the longest amongest the rest. And contrarie waies, D.B, is the shorteste, because it is farthest distaunt from D.A. And so maie you iudge of D.F, because it is nerer vnto D.A, then is D.B, therefore is it longer then D.B. And likewaies because it is farther of from D.A, then is D.E, therfore is it shorter then D.E. Now for those partes of the lines whiche bee withoute the circle (as you see) D.C, is the shortest. because it is the parte of that line which passeth by the centre, And D.K, is next to it in distance, and therefore also in shortnes, so D.G, is farthest from it in distance, and therfore is the longest of them. Now D.H, beyng nerer then D.G, is also shorter i.i. then it, and beynge farther of, then D.K, is longer then it. So that for this parte of the theoreme (as I think) you do plainly perceaue the truthe thereof, so the residue hathe no difficulte. For seing that the nearer any line is to D.C, (which ioyneth with the diameter) the shorter it is and the farther of from it, the longer it is. And seyng two lynes can not be of like distaunce beinge bothe on one side, therefore if they shal be of one lengthe, and consequently of one distaunce, they must needes bee on contrary sides of the saide line D.C. And so appeareth the meaning of the whole Theoreme.
And of this Theoreme dothe there folowe an other lyke. whiche you maye calle other a theoreme by it selfe, or else a Corollary vnto this laste theoreme, I passe not so muche for the name. But his sentence is this: when so euer any lynes be drawen frome any pointe, withoute a circle, whether they crosse the circle, or eande in the utter edge of his circumference, those two lines that bee equally distaunt from the least line are equal togither, and contrary waies, if they be equall togither, they ar also equally distant from that least line.
For the declaracion of this proposition, it shall not need to vse any other example, then that which is brought for the explication of this laste theoreme, by whiche you may without any teachinge easyly perceaue both the meanyng and also the truth of this proposition.
The Liiij. Theoreme.
If a point be set forthe in a circle, and frõ that pointe vnto the circumference many lines drawen, of which more then two are equal togither, then is that point the centre of that circle.
[i.i.v]Example.
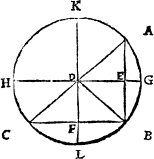
The circle is A.B.C, and within it I haue sette fourth for an example three prickes, which are D.E. and F, from euery one of them I haue drawẽ (at the leaste) iiij. lines vnto the circumference of the circle but frome D, I haue drawen more, yet maye it appear readily vnto your eye, that of all the lines whiche be drawen from E. and F, vnto the circumference, there are but twoo equall, and more can not bee, for G.E. nor E.H. hath none other equal to theim, nor canne not haue any beinge drawen from the same point E. No more can L.F, or F.K, haue anye line equall to either of theim, beinge drawen from the same pointe F. And yet from either of those two poinctes are there drawen twoo lines equall togither, as A.E, is equall to E.B, and B.F, is equall to F.C, but there can no third line be drawen equall to either of these two couples, and that is by reason that they be drawen from a pointe distaunte from the centre of the circle. But from D, althoughe there be seuen lines drawen, to the circumference, yet all bee equall, bicause it is the centre of the circle. And therefore if you drawe neuer so mannye more from it vnto the circumference, all shall be equal, so that this is the priuilege (as it were of the centre) and therfore no other point can haue aboue two equal lines drawen from it vnto the circumference. And from all pointes you maye drawe ij. equall lines to the circumference of the circle, whether that pointe be within the circle or without it.
The lv. Theoreme.
No circle canne cut an other circle in more i.ij. pointes then two.
Example.
The first circle is A.B.F.E, the second circle is B.C.D.E, and they crosse one an other in B. and in E, and in no more pointes. Nother is it possible that they should, but other figures ther be, which maye cutte a circle in foure partes, as you se in this exãple. Where I haue set forthe one tunne forme, and one eye forme, and eche of them cutteth euery of their two circles into foure partes. But as they be irregulare formes, that is to saye, suche formes as haue no precise measure nother proportion in their draughte, so can there scarcely be made any certaine theorem of them. But circles are regulare formes, that is to say, such formes as haue in their protracture a iuste and certaine proportion, so that certain and determinate truths may be affirmed of them, sith they ar vniforme and vnchaungable.
The lvi. Theoreme.
If two circles be so drawen, that the one be within the other, and that they touche one an other: If a line bee drawen by bothe their centres, and so forthe in lengthe, that line shall runne to that pointe, where the circles do touche.
[i.ii.v]
Example.
The one circle, which is the greattest and vttermost is A.B.C, the other circle that is ye lesser, and is drawen within the firste, is A.D.E. The cẽtre of the greater circle is F, and the centre of the lesser circle is G, the pointe where they touche is A. And now you may see the truthe of the theoreme so plainely, that it needeth no farther declaracion. For you maye see, that drawinge a line from F. to G, and so forth in lengthe, vntill it come to the circumference, it wyll lighte in the very poincte A, where the circles touche one an other.
The Lvij. Theoreme.
If two circles bee drawen so one withoute an other, that their edges doo touche and a right line bee drawnenne frome the centre of the one to the centre of the other, that line shall passe by the place of their touching.
Example.
The firste circle is A.B.E, and his centre is K, The secõd circle is D.B.C, and his cẽtre is H, the point wher they do touch is B. Nowe doo you se that the line K.H, whiche is drawen i.iij. from K, that is centre of the firste circle, vnto H, beyng centre of the second circle, doth passe (as it must nedes by the pointe B,) whiche is the verye poynte wher they do to touche together.
The .lviij. theoreme.
One circle can not touche an other in more pointes then one, whether they touche within or without.
Example.
For the declaration of this Theoreme, I haue drawen iiij. circles, the first is A.B.C, and his centre H. the second is A.D.G, and his centre F. the third is L.M, and his centre K. the .iiij. is D.G.L.M, and his centre E. Nowe as you perceiue the second circle A.D.G, toucheth the first in the inner side, in so much as it is drawen within the other, and yet it toucheth him but in one point, that is to say in A, so lykewaies the third circle L.M, is drawen without the firste circle and toucheth [i.iii.v] hym, as you maie see, but in one place. And now as for the .iiij. circle, it is drawen to declare the diuersitie betwene touchyng and cuttyng, or crossyng. For one circle maie crosse and cutte a great many other circles, yet can be not cutte any one in more places then two, as the fiue and fiftie Theoreme affirmeth.
The .lix. Theoreme.
In euerie circle those lines are to be counted equall, whiche are in lyke distaunce from the centre, And contrarie waies they are in lyke distance from the centre, whiche be equall.
Example.
In this figure you see firste the circle drawen, whiche is A.B.C.D, and his centre is E. In this circle also there are drawen two lines equally distaunt from the centre, for the line A.B, and the line D.C, are iuste of one distaunce from the centre, whiche is E, and therfore are they of one length. Again thei are of one lengthe (as shall be proued in the boke of profes) and therefore their distaunce from the centre is all one.
The lx. Theoreme.
In euerie circle the longest line is the diameter, and of all the other lines, thei are still longest [i.iiii.] that be nexte vnto the centre, and they be the shortest, that be farthest distaunt from it.
Example.
In this circle A.B.C.D, I haue drawen first the diameter, whiche is A.D, whiche passeth (as it must) by the centre E, Then haue I drawen ij. other lines as M.N, whiche is neerer the centre, and F.G, that is farther from the centre. The fourth line also on the other side of the diameter, that is B.C, is neerer to the centre then the line F.G, for it is of lyke distance as is the lyne M.N. Nowe saie I, that A.D, beyng the diameter, is the longest of all those lynes, and also of any other that maie be drawen within that circle, And the other line M.N, is longer then F.G. Also the line F.G, is shorter then the line B.C, for because it is farther from the centre then is the lyne B.C. And thus maie you iudge of al lines drawen in any circle, how to know the proportion of their length, by the proportion of their distance, and contrary waies, howe to discerne the proportion of their distance by their lengthes, if you knowe the proportion of their length. And to speake of it by the waie, it is a maruaylouse thyng to consider, that a man maie knowe an exacte proportion betwene two thynges, and yet can not name nor attayne the precise quantitee of those two thynges, As for exaumple, If two squares be sette foorthe, whereof the one containeth in it fiue square feete, and the other contayneth fiue and fortie foote, of like square feete, I am not able to tell, no nor yet anye manne liuyng, what is the precyse measure [i.iiii.v] of the sides of any of those .ij. squares, and yet I can proue by vnfallible reason, that their sides be in a triple proportion, that is to saie, that the side of the greater square (whiche containeth .xlv. foote) is three tymes so long iuste as the side of the lesser square, that includeth but fiue foote. But this seemeth to be spoken out of ceason in this place, therfore I will omitte it now, reseruyng the exacter declaration therof to a more conuenient place and time, and will procede with the residew of the Theoremes appointed for this boke.
The .lxi. Theoreme.
If a right line be drawen at any end of a diameter in perpendicular forme, and do make a right angle with the diameter, that right line shall light without the circle, and yet so iointly knitte to it, that it is not possible to draw any other right line betwene that saide line and the circumferẽce of the circle. And the angle that is made in the semicircle is greater then any sharpe angle that may be made of right lines, but the other angle without, is lesser then any that can be made of right lines.
Example.
In this circle A.B.C, the diameter is A.C, the perpendicular line, which maketh a right angle with the diameter, is C.A, whiche line falleth without the circle, and yet ioyneth so exactly vnto it, that it is not possible to draw an other right line betwene the circumference of the circle and it, whiche thyng k.i. is so plainly seene of the eye, that it needeth no farther declaracion. For euery man wil easily consent, that betwene the croked line A.F, (whiche is a parte of the circumferẽce of the circle) and A.E (which is the said perpẽdicular line) there can none other line bee drawen in that place where they make the angle. Nowe for the residue of the theoreme. The angle D.A.B, which is made in the semicircle, is greater then anye sharpe angle that may bee made of ryghte lines. and yet is it a sharpe angle also, in as much as it is lesser then a right angle, which is the angle E.A.D, and the residue of that right angle, which lieth without the circle, that is to saye, E.A.B, is lesser then any sharpe angle that can be made of right lines also. For as it was before rehersed, there canne no right line be drawen to the angle, betwene the circumference and the right line E.A. Then must it needes folow, that there can be made no lesser angle of righte lines. And againe, if ther canne be no lesser then the one, then doth it sone appear, that there canne be no greater then the other, for they twoo doo make the whole right angle, so that if anye corner coulde be made greater then the one parte, then shoulde the residue bee lesser then the other parte, so that other bothe partes muste be false, or els bothe graunted to be true.
The lxij. Theoreme.
If a right line doo touche a circle, and an other right line drawen frome the centre of the circle to the pointe where they touche, that [k.i.v] line whiche is drawenne frome the centre, shall be a perpendicular line to the touch line.
Example.
The circle is A.B.C, and his centre is F. The touche line is D.E, and the point wher they touch is C. Now by reason that a right line is drawen frome the centre F. vnto C, which is the point of the touche, therefore saith the theoreme, that the sayde line F.C, muste needes bee a perpendicular line vnto the touche line D.E.
The lxiij. Theoreme.
If a righte line doo touche a circle, and an other right line be drawen from the pointe of their touchinge, so that it doo make righte corners with the touche line, then shal the centre of the circle bee in that same line, so drawen.
Example.
The circle is A.B.C, and the centre of it is G. The touche line is D.C.E, and the pointe where it toucheth, is C. Nowe k.ij. it appeareth manifest, that if a righte line be drawen from the pointe where the touch line doth ioine with the circle, and that the said lyne doo make righte corners with the touche line, then muste it needes go by the centre of the circle, and then consequently it must haue the sayde cẽtre in him. For if the saide line shoulde go beside the centre, as F.C. doth, then dothe it not make righte angles with the touche line, which in the theoreme is supposed.
The lxiiij. Theoreme.
If an angle be made on the centre of a circle, and an other angle made on the circumference of the same circle, and their grounde line be one common portion of the circumference, then is the angle on the centre twise so great as the other angle on the circũferẽce.
Example.
The circle is A.B.C.D, and his centre is E: the angle on the centre is C.E.D, and the angle on the circumference is C.A.D t their commen ground line, is C.F.D. Now say I that the angle C.E.D, whiche is on the centre, is twise so greate as the angle C.A.D, which is on the circumference.
[k.ii.v]The lxv. Theoreme.
Those angles whiche be made in one cantle of a circle, must needes be equal togither.
Example.
Before I declare this theoreme by example, it shall bee needefull to declare, what is it to be vnderstande by the wordes in this theoreme. For the sentence canne not be knowen, onles the uery meaning of the wordes be firste vnderstand. Therefore when it speaketh of angles made in one cantle of a circle, it is this to be vnderstand, that the angle muste touch the circumference: and the lines that doo inclose that angle, muste be drawen to the extremities of that line, which maketh the cantle of the circle. So that if any angle do not touch the circumference, or if the lines that inclose that angle, doo not ende in the extremities of the corde line, but ende other in some other part of the said corde, or in the circumference, or that any one of them do so eande, then is not that angle accompted to be drawen in the said cantle of the circle. And this promised, nowe will I cumme to the meaninge of the theoreme. I sette forthe a circle whiche is A.B.C.D, and his centre E, in this circle I drawe a line D.C, whereby there ar made two cantels, a more and a lesser. The lesser is D.E.C, and the geater is D.A.B.C. In this greater cantle I drawe two angles, the firste is D.A.C, and the second is D.B.C which two angles by reason they are made bothe in one cantle of a circle (that is the cantle D.A.B.C) therefore are they both equall. k.iij. Now doth there appere an other triangle, whose angle lighteth on the centre of the circle, and that triangle is D.E.C, whose angle is double to the other angles, as is declared in the lxiiij. Theoreme, whiche maie stande well enough with this Theoreme, for it is not made in this cantle of the circle, as the other are, by reason that his angle doth not light in the circumference of the circle, but on the centre of it.
The .lxvi. theoreme.
Euerie figure of foure sides, drawen in a circle, hath his two contrarie angles equall vnto two right angles.
Example.
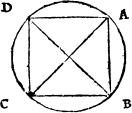
The circle is A.B.C.D, and the figure of foure sides in it, is made of the sides B.C, and C.D, and D.A, and A.B. Now if you take any two angles that be contrary, as the angle by A, and the angle by C, I saie that those .ij. be equall to .ij. right angles. Also if you take the angle by B, and the angle by D, whiche two are also contray, those two angles are like waies equall to two right angles. But if any man will take the angle by A, with the angle by B, or D, they can not be accompted contrary, no more is not the angle by C. estemed contray to the angle by B, or yet to the angle by D, for they onely be accompted contrary angles, whiche haue no one line common to them bothe. Suche is the angle by A, in respect of the angle by C, for there both lynes be distinct, where as the angle by A, and the angle by D, haue one common line A.D, and therfore can not be accompted contrary angles, So the angle by D, and the angle by C, [k.iii.v] haue D.C, as a common line, and therefore be not contrary angles. And this maie you iudge of the residewe, by like reason.
The lxvij. Theoreme.
Vpon one right lyne there can not be made two cantles of circles, like and vnequall, and drawen towarde one parte.
Example.
Cantles of circles be then called like, when the angles that are made in them be equall. But now for the Theoreme, let the right line be A.E.C, on whiche I draw a cantle of a circle, whiche is A.B.C. Now saieth the Theoreme, that it is not possible to draw an other cantle of a circle, whiche shall be vnequall vnto this first cantle, that is to say, other greatter or lesser then it, and yet be lyke it also, that is to say, that the angle in the one shall be equall to the angle in the other. For as in this example you see a lesser cantle drawen also, that is A.D.C, so if an angle were made in it, that angle would be greatter then the angle made in the cantle A.B.C, and therfore can not they be called lyke cantels, but and if any other cantle were made greater then the first, then would the angle in it be lesser then that in the firste, and so nother a lesser nother a greater cantle can be made vpon one line with an other, but it will be vnlike to it also.
The .lxviij. Theoreme.
Lyke cantelles of circles made on equal [k.iiii.] righte lynes, are equall together.
Example.
What is ment by like cantles you haue heard before. and it is easie to vnderstand, that suche figures a called equall, that be of one bygnesse, so that the one is nother greater nother lesser then the other. And in this kinde of comparison, they must so agree, that if the one be layed on the other, they shall exactly agree in all their boundes, so that nother shall excede other.
Nowe for the example of the Theoreme, I haue set forthe diuers varieties of cantles of circles, amongest which the first and seconde are made vpõ equall lines, and ar also both equall and like. The third couple ar ioyned in one, and be nother equall, nother like, but expressyng an absurde deformitee, whiche would folowe if this Theoreme wer not true. And so in the fourth couple you maie see, that because they are not equall cantles, therfore can not they be like cantles, for necessarily it goeth together, that all cantles of circles made vpon equall right lines, if they be like they must be equall also.
The lxix. Theoreme.
In equall circles, suche angles as be equall are made vpon equall arch lines of the circumference, whether the angle light on the circumference, or on the centre.
Example.
Firste I haue sette for an exaumple twoo equall circles, that [k.iiii.v] is A.B.C.D, whose centre is K, and the second circle E.F.G.H, and his centre L, and in eche of thẽ is there made two angles, one on the circumference, and the other on the centre of eche circle, and they be all made on two equall arche lines, that is B.C.D. the one, and F.G.H. the other. Now saieth the Theoreme, that if the angle B.A.D, be equall to the angle F.E.H, then are they made in equall circles, and on equall arch lines of their circumference. Also if the angle B.K.D, be equal to the angle F.L.H, then be they made on the centres of equall circles, and on equall arche lines, so that you muste compare those angles together, whiche are made both on the centres, or both on the circumference, and maie not conferre those angles, wherof one is drawen on the circumference, and the other on the centre. For euermore the angle on the centre in suche sorte shall be double to the angle on the circumference, as is declared in the three score and foure Theoreme.
The .lxx. Theoreme.
In equall circles, those angles whiche bee made on equall arche lynes, are euer equall together, whether they be made on the centre, or on the circumference.
Example.
This Theoreme doth but conuert the sentence of the last Theoreme l.i. before, and therfore is to be vnderstande by the same examples, for as that saith, that equall angles occupie equall archelynes, so this saith, that equal arche lines causeth equal angles, consideringe all other circumstances, as was taughte in the laste theoreme before, so that this theoreme dooeth affirming speake of the equalitie of those angles, of which the laste theoreme spake conditionally. And where the laste theoreme spake affirmatiuely of the arche lines, this theoreme speaketh conditionally of them, as thus: If the arche line B.C.D. be equall to the other arche line F.G.H, then is that angle B.A.D. equall to the other angle F.E.H. Or els thus may you declare it causally: Bicause the arche line B.C.D, is equal to the other arche line F.G.H, therefore is the angle B.K.D. equall to the angle F.L.H, consideringe that they are made on the centres of equall circles. And so of the other angles, bicause those two arche lines aforesaid ar equal, therfore the angle D.A.B, is equall to the angle F.E.H, for as muche as they are made on those equall arche lines, and also on the circumference of equall circles. And thus these theoremes doo one declare an other, and one verifie the other.
The lxxi. Theoreme.
In equal circles, equall right lines beinge drawen, doo cutte awaye equalle arche lines frome their circumferences, so that the greater arche line of the one is equall to the greater arche line of the other, and the lesser to the lesser.
[l.i.v]Example.
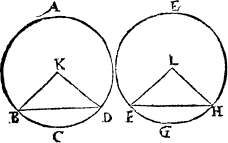
The circle A.B.C.D, is made equall to the circle E.F.G.H, and the right line B.D. is equal to the righte line F.H, wherfore it foloweth, that the ij. arche lines of the circle A.B.D, whiche are cut from his circumference by the right line B.D, are equall to two other arche lines of the circle E.F.H, being cutte frome his circumference, by the right line F.H. that is to saye, that the arche line B.A.D, beinge the greater arch line of the firste circle, is equall to the arche line F.E.H, beynge the greater arche line of the other circle. And so in like manner the lesser arche line of the firste circle, beynge B.C.D, is equal to the lesser arche line of the seconde circle, that is F.G.H.
The lxxij. Theoreme.
In equall circles, vnder equall arche lines the right lines that bee drawen are equall togither.
Example.
This Theoreme is none other, but the conuersion of the laste Theoreme beefore, and therefore needeth none other example. For as that did declare the equalitie of the arche lines, by the equalitie of the righte lines, so dothe this Theoreme l.ij. declare the equalnes of the right lines to ensue of the equalnes of the arche lines, and therefore declareth that right lyne B.D, to be equal to the other right line F.H, bicause they both are drawen vnder equall arche lines, that is to saye, the one vnder B.A.D, and thother vnder F.E.H, and those two arch lines are estimed equall by the theoreme laste before, and shal be proued in the booke of proofes.
The lxxiij. Theoreme.
In euery circle, the angle that is made in the halfe circle, is a iuste righte angle, and the angle that is made in a cantle greater then the halfe circle, is lesser thanne a righte angle, but that angle that is made in a cantle, lesser then the halfe circle, is greatter then a right angle. And moreouer the angle of the greater cantle is greater then a righte angle and the angle of the lesser cantle is lesser then a right angle.
Example.
In this proposition, it shal be meete to note, that there is a greate diuersite betwene an angle of a cantle, and an angle made in a cantle, and also betwene the angle of a semicircle, and ye angle made in a semicircle. Also it is meet to note yt al angles that be made in ye part of a circle, ar made other in a semicircle, (which is the iuste half circle) or els in a cantle of the circle, which cantle is other greater or lesser then the semicircle is, as in this figure annexed you maye perceaue euerye one of the thinges seuerallye.
[l.ii.v]
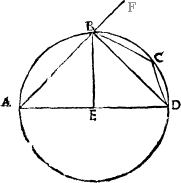
Firste the circle is, as you see, A.B.C.D, and his centre E, his diameter is A.D, Then is ther a line drawẽ from A. to B, and so forth vnto F, which is without the circle: and an other line also frome B. to D, whiche maketh two cantles of the whole circle. The greater cantle is D.A.B, and the lesser cantle is B.C.D, In whiche lesser cantle also there are two lines that make an angle, the one line is B.C, and the other line is C.D. Now to showe the difference of an angle in a cantle, and an angle of a cantle, first for an example I take the greter cãtle B.A.D, in which is but one angle made, and that is the angle by A, which is made of a line A.B, and the line A.D, And this angle is therfore called an angle in a cantle. But now the same cantle hathe two other angles, which be called the angles of that cantle, so the twoo angles made of the righte line D.B, and the arche line D.A.B, are the twoo angles of this cantle, whereof the one is by D, and the other is by B. Wher you must remẽbre, that the ãgle by D. is made of the right line B.D, and the arche line D.A. And this angle is diuided by an other right line A.E.D, which in this case must be omitted as no line. Also the ãgle by B. is made of the right line D.B, and of the arch line .B.A, & although it be deuided with ij. other right lines, of wch the one is the right line B.A, & thother the right line B.E, yet in this case they ar not to be cõsidered. And by this may you perceaue also which be the angles of the lesser cantle, the first of thẽ is made of ye right line B.D, & of ye arch line B.C, the secõd is made of the right line .D.B, & of the arch line D.C. Then ar ther ij. other lines, wch deuide those ij. corners, yt is the line B.C, & the line C.D, wch ij. lines do meet l.iij. in the poynte C, and there make an angle, whiche is called an angle made in that lesser cantle, but yet is not any angle of that cantle. And so haue you heard the difference betweene an angle in a cantle, and an angle of a cantle. And in lyke sorte shall you iudg of the ãgle made in a semicircle, whiche is distinct frõ the angles of the semicircle. For in this figure, the angles of the semicircle are those angles which be by A. and D, and be made of the right line A.D, beeyng the diameter, and of the halfe circumference of the circle, but by the angle made in the semicircle is that angle by B, whiche is made of the righte line A.B, and that other right line B.D, whiche as they mete in the circumference, and make an angle, so they ende with their other extremities at the endes of the diameter. These thynges premised, now saie I touchyng the Theoreme, that euerye angle that is made in a semicircle, is a right angle, and if it be made in any cãtle of a circle, thẽ must it neds be other a blũt ãgle, or els a sharpe angle, and in no wise a righte angle. For if the cantle wherein the angle is made, be greater then the halfe circle, then is that angle a sharpe angle. And generally the greater the cãtle is, the lesser is the angle comprised in that cantle: and contrary waies, the lesser any cantle is, the greater is the angle that is made in it. Wherfore it must nedes folowe, that the angle made in a cantle lesse then a semicircle, must nedes be greater then a right angle. So the angle by B, beyng made at the right line A.B, and the righte line B.D, is a iuste righte angle, because it is made in a semicircle. But the angle made by A, which is made of the right line A.B, and of the right line A.D, is lesser then a righte angle, and is named a sharpe angle, for as muche as it is made in a cantle of a circle, greater then a semicircle. And contrary waies, the angle by C, beyng made of the righte line B.C, and of the right line C.D, is greater then a right angle, and is named a blunte angle, because it is made in a cantle of a circle, lesser then a semicircle. But now touchyng the other angles of the cantles, I saie accordyng to the Theoreme, that the .ij. angles of the greater cantle, which are by B. and D, as is before declared, are greatter eche of them then a right angle. And the [l.iii.v] angles of the lesser cantle, whiche are by the same letters B, and D, but be on the other side of the corde, are lesser eche of them then a right angle, and be therfore sharpe corners.
The lxxiiij. Theoreme.
If a right line do touche a circle, and from the pointe where they touche, a righte lyne be drawen crosse the circle, and deuide it, the angles that the saied lyne dooeth make with the touche line, are equall to the angles whiche are made in the cantles of the same circle, on the contrarie sides of the lyne aforesaid.
Example.
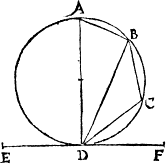
The circle is A.B.C.D, and the touche line is E.F. The pointe of the touchyng is D, from which point I suppose the line D.B, to be drawen crosse the circle, and to diuide it into .ij. cantles, wherof the greater is B.A.D, and the lesser is B.C.D, and in ech of them an angle is drawen, for in the greater cantle the angle is by A, and is made of the right lines B.A, and A.D, in the lesser cantle the angle is by C, and is made of ye right lines B.C, and C.D. Now saith the Theoreme that the angle B.D.F, is equall to the angle made in the cantle on the other side of the said line, that is to saie, in the cantle B.A.D, so that the angle B.D.F, is equall to the angle B.A.D, because the angle B.D.F, is on the one side of the line B.D, (whiche is according [l.iiii.] to the supposition of the Theoreme drawen crosse the circle) and the angle B.A.D, is in the cãtle on the other side. Likewaies the angle B.D.E, beyng on the one side of the line B.D, must be equall to the angle B.C.D, (that is the ãgle by C,) whiche is made in the cãtle on the other side of the right line B.D. The profe of all these I do reserue, as I haue often saide, to a conuenient boke, wherein they shall be all set at large.
The .lxxv. Theoreme.
In any circle when .ij. right lines do crosse one an other, the likeiamme that is made of the portions of the one line, shall be equall to the lykeiamme made of the partes of the other lyne.
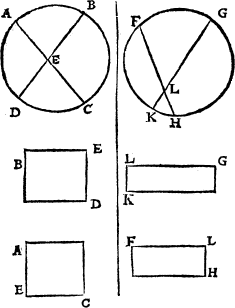
Because this Theoreme doth serue to many vses, and wold be wel vnderstande, I haue set forth .ij. examples of it. In the firste, the lines by their crossyng do make their portions somewhat toward an equalitie. In the second the portiõs of the lynes be very far frõ an equalitie, and yet in bothe these and in all other ye Theoreme is true. In the first exãple the circle is A.B.C.D, in which thone line A.C, doth crosse thother line B.D, in ye point E. Now if you do make one likeiãme or lõgsquare of D.E, & E.B, being ye .ij. [l.iiii.v] portions of the line D.B, that longsquare shall be equall to the other longsquare made of A.E, and E.C, beyng the portions of the other line A.C. Lykewaies in the second example, the circle is F.G.H.K, in whiche the line F.H, doth crosse the other line G.K, in the pointe L. Wherfore if you make a lykeiamme or longsquare of the two partes of the line F.H, that is to saye, of F.L, and L.H, that longsquare will be equall to an other longsquare made of the two partes of the line G.K. which partes are G.L, and L.K. Those longsquares haue I set foorth vnder the circles containyng their sides, that you maie somewhat whet your own wit in practisyng this Theoreme, accordyng to the doctrine of the nineteenth conclusion.
The .lxxvi. Theoreme.
If a pointe be marked without a circle, and from that pointe two right lines drawen to the circle, so that the one of them doe runne crosse the circle, and the other doe touche the circle onely, the long square that is made of that whole lyne which crosseth the circle, and the portion of it, that lyeth betwene the vtter circumference of the circle and the pointe, shall be equall to the full square of the other lyne, that onely toucheth the circle.
Example.
The circle is D.B.C, and the pointe without the circle is A, from whiche pointe there is drawen one line crosse the circle, and that is A.D.C, and an other lyne is drawn from the said m.i. pricke to the marge or edge of the circumference of the circle, and doeth only touche it, that is the line A.B. And of that first line A.D.C, you maie perceiue one part of it, whiche is A.D, to lie without the circle, betweene the vtter circumference of it, and the pointe assigned, whiche was A. Nowe concernyng the meanyng of the Theoreme, if you make a longsquare of the whole line A.C, and of that parte of it that lyeth betwene the circumference and the point, (whiche is A.D,) that longesquare shall be equall to the full square of the touche line A.B, accordyng not onely as this figure sheweth, but also the saied nyneteenth conclusion dooeth proue, if you lyste to examyne the one by the other.
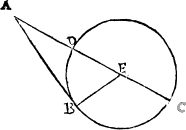 |
 |
 |
The lxxvii. Theoreme.
If a pointe be assigned without a circle, and from that pointe .ij. right lynes be drawen to the circle, so that the one doe crosse the circle, and the other dooe ende at the circumference, and that the longsquare of the line which crosseth [m.i.v] the circle made with the portiõ of the same line beyng without the circle betweene the vtter circumference and the pointe assigned, doe equally agree with the iuste square of that line that endeth at the circumference, then is that lyne so endyng on the circumference a touche line vnto that circle.
Example.
In as muche as this Theoreme is nothyng els but the sentence of the last Theoreme before conuerted, therfore it shall not be nedefull to vse any other example then the same, for as in that other Theoreme because the one line is a touche lyne, therfore it maketh a square iust equal with the longsquare made of that whole line, whiche crosseth the circle, and his portion liyng without the same circle. So saith this Theoreme: that if the iust square of the line that endeth on the circumference, be equall to that longsquare whiche is made as for his longer sides of the whole line, which commeth from the pointt assigned, and crosseth the circle, and for his other shorter sides is made of the portion of the same line, liyng betwene the circumference of the circle and the pointe assigned, then is that line whiche endeth on the circumference a right touche line, that is to saie, yf the full square of the right line A.B, be equall to the longsquare made of the whole line A.C, as one of his lines, and of his portion A.D, as his other line, then must it nedes be, that the lyne A.B, is a right touche lyne vnto the circle D.B.C. And thus for this tyme I make an ende of the Theoremes.
FINIS,
[m.ii.]
IMPRINTED at London in Poules
churcheyarde, at the signe of the Bra-
senserpent, by Reynold Wolfe.
Cum priuilegio ad imprimen-
dum solum.
ANNO DOMINI .M.D.L.I.
[m.ii.v]
Title page:
The pathway to
KNOWLEDG,
CONTAI-
NING THE FIRST PRIN-
ciples of Geometrie, as they
may moste aptly be applied vn-
to practice, bothe for vse of
instrumentes Geome-
tricall, and astrono-
micall and
also for proiection of plattes in euerye
kinde, and therfore much ne-
cessary for all sortes of
men.
Dedication:
TO THE MOST NO-
ble and puissaunt prince Edwarde the
sixte by the grace of God, of En-
gland Fraunce and Ireland kynge, de-
fendour of the faithe, and of the
Churche of England and Ire-
lande in earth the su-
preme head.
Title page of Second Book:
THE SECOND BOOKE
OF THE PRINCIPLES
of Geometry, containing certaine
Theoremes, whiche may be cal-
led Approued truthes. And be as
it were the moste certaine
groundes, wheron the
practike cõclusions
of Geometry ar
founded.
[Leaf]
Whervnto are annexed certaine declarations by
examples, for the right vnderstanding of the
same, to the ende that the simple reader
might not iustly cõplain of hardnes
or obscuritee, and for the same
cause ar the demonstra-
tions and iust profes
omitted, vntill a
more conueni-
ent time.
1551.
“Theorems of Geometry”:
The Theoremes of Geometry, before
WHICHE ARE SET FORTHE
certaine grauntable requestes
which serue for demonstrations
Mathematicall.
Transcriber’s Notes
Terminology
Corrections
Illustrations
Notes
Greek
Language and Typography
This information is for readers who know more about geometry than about mid-16th-century English.
The letters u and v follow the conventional “initial v, non-initial u” pattern except in numbers (xv, iv). The lower-case j form occurs only as the last digit of a number (ij, xxj); upper-case I and J share a form, always read as I. Italic double s was printed as an ſ+s ligature, similar to the German ß; it is shown as simple “ss”. Capital and lower-case w were often used interchangeably. Words split across line breaks may or may not have a hyphen.
The word “other” is used interchangeably with both “or” and “either”; similarly, “nother” is used in place of “nor” and “neither”. The expression “an other” is almost always written as two words.
The spellings “then(ne)” and “than(ne)” are used interchangeably; “than(ne)” is rare. The spelling “liyng”, both by itself and as the end of a longer word, is used consistently.
Terminology
Explanations of these terms are scattered through the book. They are grouped here for convenience.
| right line | straight line |
| gemow (line) | parallel |
square |
quadrilateral |
| likeiamme | parallelogram |
| longsquare | rectangle |
| touch line | tangent |
| cantle | segment of a circle |
Corrections
Unless otherwise noted, spelling, punctuation and capitalization are unchanged. Forms were regularized only where there was a very large disparity between the expected form and the apparent errors (for example, a thousand “A.B” against a dozen “A,B”), or a flagrant misprint such as “cnt” for “cut”.
Number forms such as “those. ij. last” or “line. A.B.” were silently regularized to “those .ij. last” and “line .A.B.” Missing sentence-final periods at the end of a printed line were silently supplied.
Unusual forms or combinations—especially phrase breaks where a comma is followed by a capital letter, or a period by a lower-case letter—are unchanged but noted with popups.
Illustrations
A number of illustrations contain errors such as unmarked or mislabeled points (“circle B.C.D” where only C and D are labeled). Labels added by the transcriber are shown in grey; moved or transposed labels are shown in red, with mouse-hover explanation.
Notes
1) if they can with their wysedome ouercome all vyces. Of the firste of those three sortes
Text reads “... their rwysedome ... / ... those th ee sortes ...” on consecutive lines:

2) Pagination as shown by signature numbers demands another leaf (two pages) between the end of the Preface and the beginning of the body text. But no text is missing, and the facsimile has no blank pages.
3) and yet the ij. lesser sides togither ar greater then it.
Text reads “... yet thr / ... ar greate” at consecutive line-ends:

Greek
All Greek is shown as printed. Errors or anomalies include missing, misplaced or incorrect diacritics; the letterform σ for ς; and word-final μ (mu) for ν (nu).
ἐίπερ γὰρ ἀδικεῖμ χρὴ, τυραννΐδος περῒ κάλλιστομ ἀδικεῖμ, τ’ ἄλλα δ’ ἐυσεβεῖμ χρεῶμ
eiper gar adikeim chrê, turannidos peri kallistom adikeim, t’ alla d’ eusebeim chreôm.
Φΐλιππος Αριστοτέλει χαίρειμ.
ἔσθι μοι γεγονότα ὑομ. πολλὴμ οὖμ τοῖσ θεοῖσ χάριμ ἔχω, ὀυχ ὅυτωσ ἐπῒ τῆ γεννήσει του παιδόσ, ὡσ ἐπῒ τῷ κατὰ τὴμ σὴμ ἡλικῒαμ αὐτόμ γεγονέναι ἐλπΐζω γὰρ αὐτὸμ ὑπὸ σοῦ γραφέντα καὶ παιδευθέντα ἄξιομ ἔσεσθαι καὶ ἑιμῶμ καὶ τῆς τῶμ τραγμάτωμ διαδοχῆσ.
Philippos Aristotelei chaireim.
esthi moi gegonota huom. pollêm oum tois theois charim echô, ouch houtôs epi tê gennêsei tou paidos, hôs epi tô kata têm sêm hêlikiam autom gegonenai elpizô gar autom hupo sou graphenta kai paideuthenta axiom esesthai kai heimôm kai tês tôm pragmatôm diadochês.
Ἄλέζανδρος Αρισοτέλει εὖ πράττειμ.
Ὂυκ ὀρθῶσ ἐπόιησασ ἐκδοὺσ τοὺσ ἀκροαματικόυσ τῶμ λόγωμ, τΐνι γὰρ διοισομην ἡμεῖσ τῶμ ἄλλωμ, ἐι καθ’ οὕσ ἐπαιδεύθημεν λόγουσ, ὅυτοι πάντωμ ἔσονταιν κοινόι, ἐγὼ δὲ βουλοί μημ ἅμ ταῖσ περι τὰ ἄριστα ἐμπειρΐαισ, ἢ τὰισ δυνάμεσι διαφέριμ. ἔρρωσο.
Alezandros Arisotelei eu pratteim.
Ouk orthôs epoiêsas ekdous tous akroamatikous tôm logôm, tini gar dioisomên hêmeis tôm allôm, ei kath’ hous epaideuthêmen logous, houtoi pantôm esontai koinoi, egô de bouloi mêm am tais peri ta arista empeiriais, ê tais dunamesi diapherim. errôso.


