

STELLAR ATMOSPHERES
HARVARD OBSERVATORY MONOGRAPHS
HARLOW SHAPLEY, EDITOR
No. 1
A CONTRIBUTION TO THE OBSERVATIONAL STUDY OF HIGH TEMPERATURE IN THE REVERSING LAYERS OF STARS
BY
CECILIA H. PAYNE
PUBLISHED BY THE OBSERVATORY
CAMBRIDGE, MASSACHUSETTS
1925
COPYRIGHT, 1925
BY HARVARD OBSERVATORY
PRINTED AT THE HARVARD UNIVERSITY PRESS
CAMBRIDGE, MASS., U.S.A.
[Pg v]
THE most effective way of publishing the results of astronomical investigations is clearly dependent on the nature and scope of each particular research. The Harvard Observatory has used various forms. Nearly a hundred volumes of Annals contain, for the most part, tabular material presenting observational results on the positions, photometry, and spectroscopy of stars, nebulae, and planets. Shorter investigations have been reported in Circulars, Bulletins, and in current scientific journals from which Reprints are obtained and issued serially.
It now appears that a few extensive investigations of a somewhat monographic nature can be most conveniently presented as books, the first of which is the present special analysis of stellar spectra by Miss Payne. Other volumes in this series, it is hoped, will be issued during the next few years, each dealing with a subject in which a large amount of original investigation is being carried on at this observatory.
The Monographs will differ in another respect from all the publications previously issued from the Harvard Observatory—they cannot be distributed gratis to observatories and other interested scientific institutions. It is planned, however, to cover a part of the expenses of publication with special funds and to sell the volumes at less than the cost of production.
The varied problems of stellar atmospheres are particularly suited to the comprehensive treatment here given. They involve investigations of critical potentials, spectral classification, stellar temperatures, the abundance of elements, and the far-reaching theories of thermal ionization as developed in the last few years by Saha and by Fowler and Milne. Some problems of special interest to chemists and physicists are considered, and subjects intimately bound up with inquiries concerning stellar evolution come under discussion.
[Pg vi]
The work is believed to be fairly complete from the bibliographic standpoint, for Miss Payne has endeavored throughout to give a synopsis of the relevant contributions by various investigators. Her own contributions enter all chapters and form a considerable portion of Parts II and III.
It should be remembered that the interpretation of stellar spectra from the standpoint of thermal-ionization is new and the methods employed are as yet relatively primitive. We are only at the beginning of the astronomical application of the methods arising from the newer analyses of atoms. Hence we must expect (and endeavor to provide) that a study such as is presented here will promptly need revision and extension in many places. Nevertheless, as it stands, it shows the current state of the general problem, and will also serve, we hope, as a summary of past investigations and an indication of the direction to go in the immediate future.
In the course of her investigation of stellar atmospheres, Miss Payne has had the advantage of conferences with Professors Russell and Stewart of Princeton University and Professor Saunders of Harvard University, as well as with various members of the Harvard Observatory staff.
The book has been accepted as a thesis fulfilling the requirements for the degree of Doctor of Philosophy in Radcliffe College.
H. S.
MAY 1, 1925.
[Pg vii]
| PART I | |
| THE PHYSICAL GROUNDWORK | |
| I. THE LABORATORY BASIS OF ASTROPHYSICS | 3 |
| Relation of physics to astrophysics. Properties of matter associated with nuclear structure. Arrangement of extra-nuclear electrons. Critical potentials. Duration of atomic states. Relative probabilities of atomic states. Effect on the spectrum of conditions at the source. (a) Temperature class. (b) Pressure effects. (c) Zeemann effect. (d) Stark effect. |
|
| II. THE STELLAR TEMPERATURE SCALE | 27 |
| Definitions. The mean temperature scale. Temperatures of individual stars. Differences in temperature between giants and dwarfs The temperature scale based on ionization. |
|
| III. PRESSURES IN STELLAR ATMOSPHERES | 34 |
| Range in stellar pressures. Measures of pressure in the reversing layer. (a) Pressure shifts of spectral lines. (b) Sharpness of lines. (c) Widths of lines. (d) Flash spectrum. (e) Equilibrium of outer layers of the sun. (f) Observed limit of the Balmer series. (g) Ionization phenomena. |
|
| IV. THE SOURCE AND COMPOSITION OF THE STELLAR SPECTRUM | 46 |
| General appearance of the stellar spectrum. Descriptive definitions. The continuous background. The reversing layer. Emission lines. |
|
| V. ELEMENTS AND COMPOUNDS IN STELLAR ATMOSPHERES | 55 |
| Identifications with laboratory spectra. Occurrence and behavior of known lines in stellar spectra. [Pg viii] |
|
| PART II | |
| THEORY OF THERMAL IONIZATION | |
| VI. THE HIGH-TEMPERATURE ABSORPTION SPECTRUM OF A GAS | 91 |
| The schematic reversing layer. The absorption of radiation. Low temperature conditions. Ultimate lines. Ionization. Production of subordinate lines. Lines of ionized atoms. Summary. |
|
| VII. CRITICAL DISCUSSION OF IONIZATION THEORY | 105 |
| Saha’s treatment—marginal appearance. Theoretical formulae. Physical constants required by the formulae. Assumptions necessary for the application. Laboratory evidence bearing on the theory. (a) Ultimate lines. (b) Temperature classes. (c) Furnace experiments. (d) Conductivity of flames. Solar intensities as a test of ionization theory. |
|
| VIII. OBSERVATIONAL MATERIAL FOR THE TEST OF IONIZATION THEORY | 116 |
| Measurement of line intensity. Method of standardization. Summary of results. Consistency of results. |
|
| IX. THE IONIZATION TEMPERATURE SCALE | 133 |
| Consistency of the preliminary scale. Effect of pressure. Levels of origin of ultimate and subordinate lines. Influence of relative abundance. Method of determining effective partial pressure. The corrected temperature scale. [Pg ix] |
|
| X. THE IONIZATION TEMPERATURE SCALE | 133 |
| PART III | |
| ADDITIONAL DEDUCTIONS FROM IONIZATION THEORY | |
| XI. THE ASTROPHYSICAL EVALUATION OF PHYSICAL CONSTANTS | 155 |
| Spectroscopic constants (Plaskett). Critical potentials (Payne). Duration of atomic states (Milne). |
|
| XII. SPECIAL PROBLEMS IN STELLAR ATMOSPHERES | 161 |
| Class Class The Balmer lines. Classification of Silicon and Strontium stars. Peculiar Class c-stars. |
|
| XIII. THE RELATIVE ABUNDANCE OF THE ELEMENTS | 177 |
| Terrestrial data. Astrophysical data. Uniformity of composition of stellar atmospheres. Marginal appearance. Comparison of stellar and terrestrial estimates. |
|
| XIV. THE MEANING OF STELLAR CLASSIFICATION | 190 |
| Principles of classification. Object of the Draper Classification. Method of classifying. Finer Subdivisions of the Draper Classes. Implications of the Draper system. Homogeneity of the classes. Spectral differences between giants and dwarfs. |
|
| XV. ON THE FUTURE OF THE PROBLEM | 199 |
| APPENDICES | |
| I. INDEX TO DEFINITIONS | 203 |
| II. SERIES RELATIONS IN LINE SPECTRA | 203 |
| III. LIST OF STARS USED IN CHAPTER VIII | 205 |
| IV. INTENSITY CHANGES OF LINES WITH UNKNOWN SERIES RELATIONS | 207 |
| V. MATERIAL ON A STARS, QUOTED IN CHAPTER XII | 208 |
| SUBJECT INDEX | 211 |
| NAME INDEX | 214 |
[Pg 3]
THE application of physics in the domain of astronomy constitutes a line of investigation that seems to possess almost unbounded possibilities. In the stars we examine matter in quantities and under conditions unattainable in the laboratory. The increase in scope is counterbalanced, however, by a serious limitation—the stars are not accessible to experiment, only to observation, and there is no very direct way to establish the validity of laws, deduced in the laboratory, when they are extrapolated to stellar conditions.
The verification of physical laws is not, however, the primary object of the application of physics to the stars. The astrophysicist is generally obliged to assume their validity in applying them to stellar conditions. Ultimately it may be that the consistency of the findings in different branches of astrophysics will form a basis for a more general verification of physical laws than can be attained in the laboratory; but at present, terrestrial physics must be the groundwork of the study of stellar conditions. Hence it is necessary for the astrophysicist to have ready for application the latest data in every relevant branch of physical science, realizing which parts of modern physical theory are still in a tentative stage, and exercising due caution in applying these to cosmical problems.
The recent advance of astrophysics has been greatly assisted by the development, during the last decade, of atomic and radiation theory. The claim that it would have been possible to predict the existence, masses, temperatures, and luminosities of the stars from the laws of radiation, without recourse to stellar observations, represents the triumph of the theory of radiation. It is equally true that the main features of the spectra of the stars could be predicted from a knowledge of atomic structure and the origin of spectra. The theory of [Pg 4] radiation has permitted an analysis of the central conditions of stars, while atomic theory enables us to analyze the only portion of the star that can be directly observed—the exceedingly tenuous atmosphere.
The present book is concerned with the second of these two problems, the analysis of the superficial layers, and it approaches the subject of the physical chemistry of stellar atmospheres by treating terrestrial physics as the basis of cosmical physics. From a brief working summary of useful physical data (Chapter I) and a synopsis of the conditions under which the application is to be made (Chapters II and Chapter III), we shall pass to an analysis of stellar atmospheres by means of modern spectrum theory. The standpoint adopted is primarily observational, and new data obtained by the writer in the course of the investigation will be presented as part of the discussion.
The first chapter contains a synopsis of the chief data which bear on atomic structure—the nuclear properties, and the disposition of the electrons around the nucleus. The origin of line spectra is discussed, and the ionization potentials corresponding to different atoms are tabulated. Lastly a brief summary is made of the effect of external conditions, such as temperature, pressure, and magnetic or electric fields, upon a line spectrum.
ATOMIC PROPERTIES ASSOCIATED WITH THE NUCLEUS
The properties determined by the atomic nucleus are the mass, and the isotopic and radioactive properties. The astrophysical study of these factors is as yet in an elementary stage, but it seems that all three have a bearing on the frequency of atomic species, and that future theory may also relate them to the problem of the source and fate of stellar energy. Moreover, up to the present no general formulation of the theory of the formation and stability of the elements has been possible, and it is well to keep in mind the data which are apparently most relevant to the problem—the observational facts relating to the nucleus. Probably the study of the nucleus involves the most fundamental[Pg 5] of all cosmical problems—a problem, moreover, which is largely in the hands of the laboratory physicist.
The chief nuclear data are summarized in Table I. Successive columns contain the atomic number, the element and its chemical symbol, the atomic weight[1] and the mass numbers of the known isotopes,[2] the percentage terrestrial abundance,[3] expressed in atoms, and the recorded stellar occurrence. Presence in the stars is indicated by an asterisk, absence by a dash.
| No. | Element | Atomic Weight |
Isotopes | Percentage Terrestrial Abundance (Atoms) |
Stellar Occurrences |
|
|---|---|---|---|---|---|---|
| 1 | Hydrogen | H | 1.008 | 1.008 | 15.459 | * |
| 2 | Helium | He | 4.00 | 4 | .. | * |
| 3 | Lithium | Li | 6.94 | 7, 6 | 0.0129 | * |
| 4 | Beryllium | Be | 9.01 | 9 | 0.0020 | — |
| 5 | Boron | B | 11.0 | 11, 10 | 0.0016 | — |
| 6 | Carbon | C | 12.005 | 12 | 0.2069 | * |
| 7 | Nitrogen | N | 14.01 | 14 | 0.0383 | * |
| 8 | Oxygen | O | 16.00 | 16 | 59.940 | * |
| 9 | Fluorine | F | 19.0 | 19 | 0.0282 | — |
| 10 | Neon | Ne | 20.0 | 20, 22, (21) | .. | — |
| 11 | Sodium | Na | 23.00 | 23 | 2.028 | * |
| 12 | Magnesium | Mg | 24.32 | 24, 25, 26 | 1.426 | * |
| 13 | Aluminium | Al | 27.1 | 4.946 | * | |
| 14 | Silicon | Si | 28.3 | 28, 29, 30 | 16.235 | * |
| 15 | Phosphorus | P | 31.04 | 31 | 0.0818 | — |
| 16 | Sulphur | S | 32.06 | 32 | 0.0518 | * |
| 17 | Chlorine | Cl | 35.46 | 35, 37, (39) | 0.1149 | — |
| 18 | Argon | A | 39.88 | 40, 36 | .. | — |
| 19 | Potassium | K | 39.10 | 39, 41 | 1.088 | * |
| 20 | Calcium | Ca | 40.07 | (40, 44) | 1.503 | * |
| 21 | Scandium | Sc | 44.1 | 45 | .. | * |
| 22 | Titanium | Ti | 48.1 | 48 | 0.2407 | * |
| 23 | Vanadium | V | 51.0 | 51 | 0.0133 | * [Pg 6] |
| 24 | Chromium | Cr | 52.0 | 52 | 0.0213 | * |
| 25 | Manganese | Mn | 54.93 | 55 | 0.0351 | * |
| 26 | Iron | Fe | 55.84 | 54, 56 | 1.485 | * |
| 27 | Cobalt | Co | 58.97 | 59 | 0.0009 | * |
| 28 | Nickel | Ni | 58.68 | 58, 60 | 0.0091 | * |
| 29 | Copper | Cu | 63.57 | 63, 65 | 0.0028 | * |
| 30 | Zinc | Zn | 65.37 | (64, 66, 68, 70) | 0.0011 | * |
| 31 | Gallium | Ga | 69.9 | 69, 71 | .. | — |
| 32 | Germanium | Ge | 72.5 | 74, 72, 70 | .. | — |
| 33 | Arsenic | As | 74.96 | 75 | .. | — |
| 34 | Selenium | Se | 79.2 | .. | — | |
| 35 | Bromine | Br | 79.92 | 79, 81 | .. | — |
| 36 | Krypton | Kr | 82.92 | 84, 86, 82, 83, 70, 78 |
.. | — |
| 37 | Rubidium | Rb | 85.45 | 85, 87 | .. | * |
| 38 | Strontium | Sr | 87.63 | 88, 86 | 0.0065 | * |
| 39 | Yttrium | Y | 88.7 | 89 | 0.0030 (with Ce) |
* |
| 40 | Zirconium | Z | 90.6 | 90, 92, 94 | 0.0095 | * |
| 41 | Niobium | Nb | 93.1 | .. | ? | |
| 42 | Molybdenum | Mo | 96 | .. | * | |
| 43 | .. | .. | .. | |||
| 44 | Ruthenium | Ru | 101.7 | .. | * | |
| 45 | Rhodium | Rh | 102.9 | .. | * | |
| 46 | Palladium | Pd | 106.7 | .. | * | |
| 47 | Silver | Ag | 107.88 | 107, 109 | .. | * |
| 48 | Cadmium | Cd | 112.40 | 110, 111, 112, 113, 114, 116 |
.. | — |
| 49 | Indium | In | 114.8 | .. | — | |
| 50 | Tin | Sn | 118.7 | .. | ? | |
| 51 | Antimony | Sb | 120.2 | .. | — | |
| 52 | Tellurium | Te | 127.5 | 126, 128, 130 | .. | — |
| 53 | Iodine | I | 126.92 | 127 | .. | — |
| 54 | Xenon | Xe | 130.2 | 129, 132, 131, 134, 136, (128, 130) |
.. | — |
| 55 | Caesium | Cs | 132.81 | 133 | .. | * |
| 56 | Barium | Ba | 137.37 | 138 | 0.0098 | * |
| 57 | Lanthanum | La | 139.0 | 139 | .. | * |
| 58 | Cerium | Ce | 140.25 | 140, 142 | 0.0030 (with Y) |
* |
| 59 | Praseodymium | Pr | 140.9 | 141 | .. | —[Pg 7] |
| 60 | Neodymium | Nd | 144.3 | 142-150 | .. | — |
| 61 | .. | .. | .. | .. | ||
| 62 | Samarium | Sa | 150.4 | .. | — | |
| 63 | Europium | Eu | 152.0 | .. | * | |
| 64 | Gadolinium | Gd | 157.3 | .. | — | |
| 65 | Terbium | Tb | 159.2 | .. | * | |
| 66 | Dysprosium | Dy | 162.5 | .. | — | |
| 67 | Holmium | Ho | 163.5 | .. | — | |
| 68 | Erbium | Er | 167.7 | .. | — | |
| 69 | Thulium | Tm | 168.5 | .. | — | |
| 70 | Ytterbium | Yb | 173.5 | .. | — | |
| 71 | Lutecium | Lu | 175.0 | .. | — | |
| 72 | Hafnium | Hf | .. | — | ||
| 73 | Tantalum | Ta | 181.5 | .. | — | |
| 74 | Tungsten | W | 184.0 | .. | — | |
| 75 | .. | .. | — | |||
| 76 | Osmium | Os | 190.9 | .. | — | |
| 77 | Iridium | Ir | 193.1 | .. | — | |
| 78 | Platinum | Pt | 195.2 | .. | — | |
| 79 | Gold | Au | 197.2 | .. | — | |
| 80 | Mercury | Hg | 200.6 | (197, 198, 199, 200) 202, 204 |
.. | — |
| 81 | Thallium | Tl | 204.0 | .. | — | |
| 82 | Lead | Pb | 207.2 | 0.0002 | * | |
| 83 | Bismuth | Bi | 208.0 | .. | — | |
| 84 | .. | .. | .. | .. | ||
| 85 | .. | .. | .. | .. | ||
| 86 | Radon | Rd | 222.4 | .. | — | |
| 87 | .. | .. | .. | .. | ||
| 88 | Radium | Ra | 226.0 | .. | — | |
| 89 | .. | .. | .. | .. | ||
| 90 | Thorium | Th | 232.4 | .. | — | |
| 91 | .. | .. | .. | .. | ||
| 92 | Uranium | U | 238.2 | .. | [Pg 8]— | |
ARRANGEMENT OF EXTRA-NUCLEAR ELECTRONS
Logically a description of the analysis of spectra should precede the discussion of electron arrangement, for our knowledge of the extra-nuclear electrons is very largely based on spectroscopic evidence. The established conceptions of atomic structure, however, are useful in classifying mentally the general outlines of the origin of line spectra, and therefore, for convenience of reference, Bohr’s table[4] of the arrangement of extra-nuclear electrons is here prefixed to our brief discussion of spectroscopic data. The chemical elements are given in order of atomic number, and successive columns contain, for the atom in its normal state, the numbers of electrons in the various quantum orbits.
Figure 1
Arrangement of electron orbits for the atom of neutral sodium.
Orbits consisting partly of broken lines are circular orbits seen in
perspective. The numbers and quantum relations of the orbits are as
follows: inner shell, two orbits; next shell, four
orbits and four
orbits; outer electron
orbit.
In accordance with the notation of Bohr and Kramers,[5] the first figure in the orbit-designation that stands at the head of a column denotes the total quantum number, which determines the length of the major axis of the corresponding orbit. The subscript is the so-called azimuthal quantum number, which determines the ellipticity of the orbit; the orbits with the smallest azimuthal quantum numbers are the most eccentric, and those for which the azimuthal quantum number is [Pg 9] equal to the total quantum number are circular. The diagram (Figure 1) represents the normal arrangement of electrons around the nucleus of the sodium atom, which possesses eleven extra-nuclear electrons.
| No. | Elt. | 1₁ | 2₁ | 2₂ | 3₁ | 3₂ | 3₃ | 4₁ | 4₂ | 4₃ | 4₄ | 5₁ | 5₂ | 5₃ | 5₄ | 5₅ | 6₁ | 6₂ | 6₃ | 6₄ | 6₅ | 6₆ | 7₁ | 7₂ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | H | 1 | ||||||||||||||||||||||
| 2 | He | 2 | ||||||||||||||||||||||
| 3 | Li | 2 | 1 | |||||||||||||||||||||
| 4 | Be | 2 | 2 | |||||||||||||||||||||
| 5 | B | 2 | 2 | (1) | ||||||||||||||||||||
| 6 | C | 2 | 2 | 2 | ||||||||||||||||||||
| 7 | N | 2 | 4 | 1 | ||||||||||||||||||||
| 8 | O | 2 | 4 | 2 | ||||||||||||||||||||
| 9 | F | 2 | 4 | 3 | ||||||||||||||||||||
| 10 | Ne | 2 | 4 | 4 | ||||||||||||||||||||
| 11 | Na | 2 | 4 | 4 | 1 | |||||||||||||||||||
| 12 | Mg | 2 | 4 | 4 | 2 | |||||||||||||||||||
| 13 | Al | 2 | 4 | 4 | 2 | 1 | ||||||||||||||||||
| 14 | Si | 2 | 4 | 4 | (2) | (2) | ||||||||||||||||||
| 15 | P | 2 | 4 | 4 | 4 | 1 | ||||||||||||||||||
| 16 | S | 2 | 4 | 4 | 4 | 2 | ||||||||||||||||||
| 17 | Cl | 2 | 4 | 4 | 4 | 3 | ||||||||||||||||||
| 18 | A | 2 | 4 | 4 | 4 | 4 | ||||||||||||||||||
| 19 | K | 2 | 4 | 4 | 4 | 4 | - | 1 | ||||||||||||||||
| 20 | Ca | 2 | 4 | 4 | 4 | 4 | - | 2 | ||||||||||||||||
| 21 | Sc | 2 | 4 | 4 | 4 | 4 | 1 | (2) | ||||||||||||||||
| 22 | Ti | 2 | 4 | 4 | 4 | 4 | 2 | (2) | ||||||||||||||||
| 29 | Cu | 2 | 4 | 4 | 6 | 6 | 6 | 1 | ||||||||||||||||
| 30 | Zn | 2 | 4 | 4 | 6 | 6 | 6 | 2 | ||||||||||||||||
| 31 | Ga | 2 | 4 | 4 | 6 | 6 | 6 | 2 | 1 | |||||||||||||||
| 32 | Ge | 2 | 4 | 4 | 6 | 6 | 6 | 4 | ||||||||||||||||
| 33 | As | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 1 | |||||||||||||||
| 34 | Se | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 2 | |||||||||||||||
| 36 | Kr | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 3 | |||||||||||||||
| 37 | Rb | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 4 | - | - | 1 | ||||||||||||
| 38 | Sr | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 4 | - | - | 2 | ||||||||||||
| 39 | Y | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 4 | 1 | - | (2) | ||||||||||||
| 40 | Zr | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 4 | 2 | - | (2) | [Pg 10] | |||||||||||
| 47 | Ag | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 1 | ||||||||||||
| 48 | Cd | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 2 | ||||||||||||
| 49 | In | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 2 | 1 | |||||||||||
| 50 | Sn | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | ||||||||||||
| 51 | Sb | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 1 | |||||||||||
| 52 | Te | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 2 | |||||||||||
| 53 | I | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 3 | |||||||||||
| 54 | Xe | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 4 | |||||||||||
| 55 | Cs | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 4 | - | - | - | 1 | |||||||
| 56 | Ba | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 4 | - | - | - | 2 | |||||||
| 57 | La | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 4 | 1 | - | - | (2) | |||||||
| 58 | Ce | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - | 4 | 4 | 2 | - | - | (2) | |||||||
| 59 | Pr | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 2 | 4 | 4 | 3 | - | - | 1 | |||||||
| 71 | Lu | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 4 | 4 | 1 | - | - | (2) | |||||||
| 72 | Hf | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 4 | 4 | 2 | - | - | (2) | |||||||
| 79 | Au | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 1 | |||||||
| 80 | Hg | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 2 | |||||||
| 81 | Ti | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 2 | 1 | ||||||
| 82 | Pb | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | (4) | |||||||
| 83 | Bi | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 4 | 1 | ||||||
| 86 | Rd | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 4 | 4 | ||||||
| 88 | Ra | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 4 | 4 | - | - | - | - | 2 | |
| 89 | Ac | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 4 | 4 | 1 | - | - | - | (2) | |
| 90 | Th | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | - | - | 4 | 4 | 2 | - | - | - | (2) | |
| 118 | ? | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | - | 6 | 6 | 6 | - | - | - | 4 | 4 |
The table also gives the number of spectroscopic valency electrons, a quantity which is required by the theory of thermal ionization. The spectroscopic valency electrons are those in equivalent outer orbits (outer orbits of equal total quantum number which have the same azimuthal quantum number). The number is not necessarily the same as the number of chemical valencies (the number of orbits with the same total quantum number) although the two values coincide for the alkali metals and for the alkaline earths. For carbon,[6] on the other [Pg 11] hand, the number of spectroscopic valency electrons is two (the number of 22 orbits), while the chemical valency, corresponding to the total number of 2-quantum orbits, is four.
THE PRODUCTION OF LINE SPECTRA
It is not proposed to discuss the theory of the origin of line spectra here in any detail. What is important from the astrophysical point of view is the association of known lines in the spectrum with different levels of energy in the atom, these levels representing definite electron orbits. Absorption and emission of energy take place in an atom by the transfer of an electron from an orbit associated with low energy to an orbit associated with high energy, and vice versa. The frequency of the light which is thus absorbed or emitted is expressed by the familiar quantum relation:
where
and
are the initial and final energies,
, and
is the frequency of the light absorbed or given out.
The atom absorbs from its environment the quanta relevant to the particular electron transfers of which it is capable at the time. These transfers are, of course, governed by the number and arrangement of the spectroscopic valency electrons, or in other words, by the state of ionization or excitation of the atom.
The unionized (or neutral) atom in the unexcited state absorbs the ultimate lines by the removal of one electron from its normal stationary state to some other which can be reached from that state, and re-emits them by the return of the electron to that state. The electron may, of course, leave the state to which it was carried by the ultimate absorption and pass to some state other than the normal one. If this final state is a state of higher energy than the previous state, the line produced by the process will be an absorption line; if [Pg 12] it is of lower energy the result will be the production of an emission line. In either case the line produced by the transfer of an electron from a stationary state other than the normal state is known as a subordinate line. The distinction between series of ultimate and subordinate lines is of great importance in the astrophysical applications of the theory of ionization.
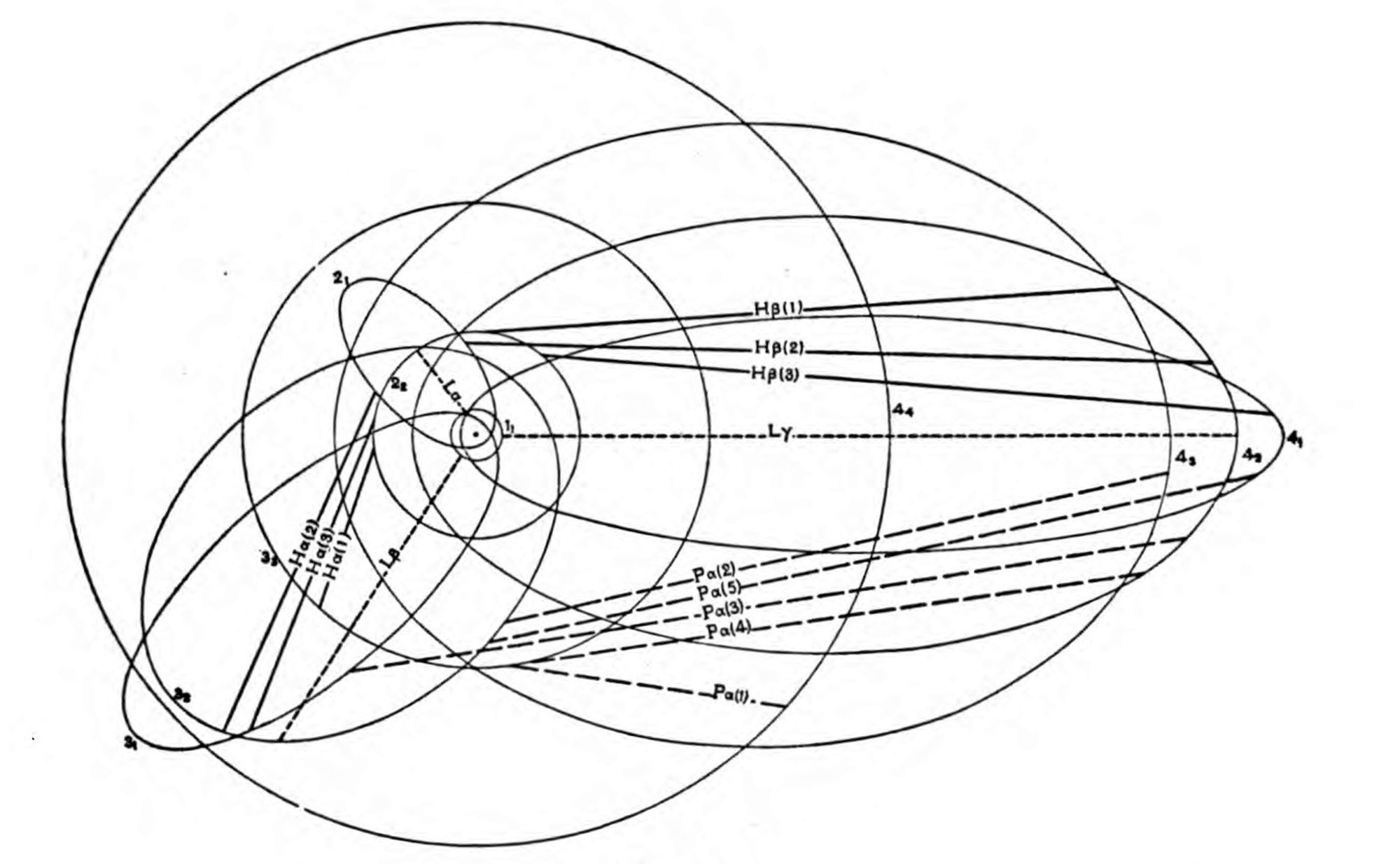
Figure 2
The hydrogen atom. The ten innermost orbits possible for the single electron of the atom of hydrogen are diagrammatically represented. All possible quantum transitions between the orbits are indicated as follows:—short dashes, Lyman series, terminating at a 1-quantum orbit; full lines, Balmer series, terminating at a 2-quantum orbit; long dashes, Paschen series, terminating at a 3-quantum orbit. Transfers are only possible between orbits with azimuthal quantum numbers differing by ±1.
When the energy supply from the environment is great enough,
the “outermost” (or most easily detachable) valency electron is
entirely removed by the energy absorbed. In consequence the atom is
superficially transformed, giving rise to a totally new spectrum,
which strongly resembles the spectrum of the atom next preceding in
the periodic system. Bohr’s table embodies the interpretation of
[Pg 13]
this resemblance—the so-called Displacement Rule of Kossell and
Sommerfeld[7]—which has recently been strikingly confirmed by a very
complete investigation of the arc and spark (neutral and ionized)
spectra of the atoms in the first long period.[8] It may be seen at
once, for instance, that the removal of the outermost (or )
electron from the atom of aluminum (
) produces an arrangement
of external electrons identical with that for magnesium (
). The
ionized atom produced by the complete removal of one electron gives,
like the neutral atom, two kinds of line spectrum—the ultimate lines
and the subordinate lines.
[Pg 14]
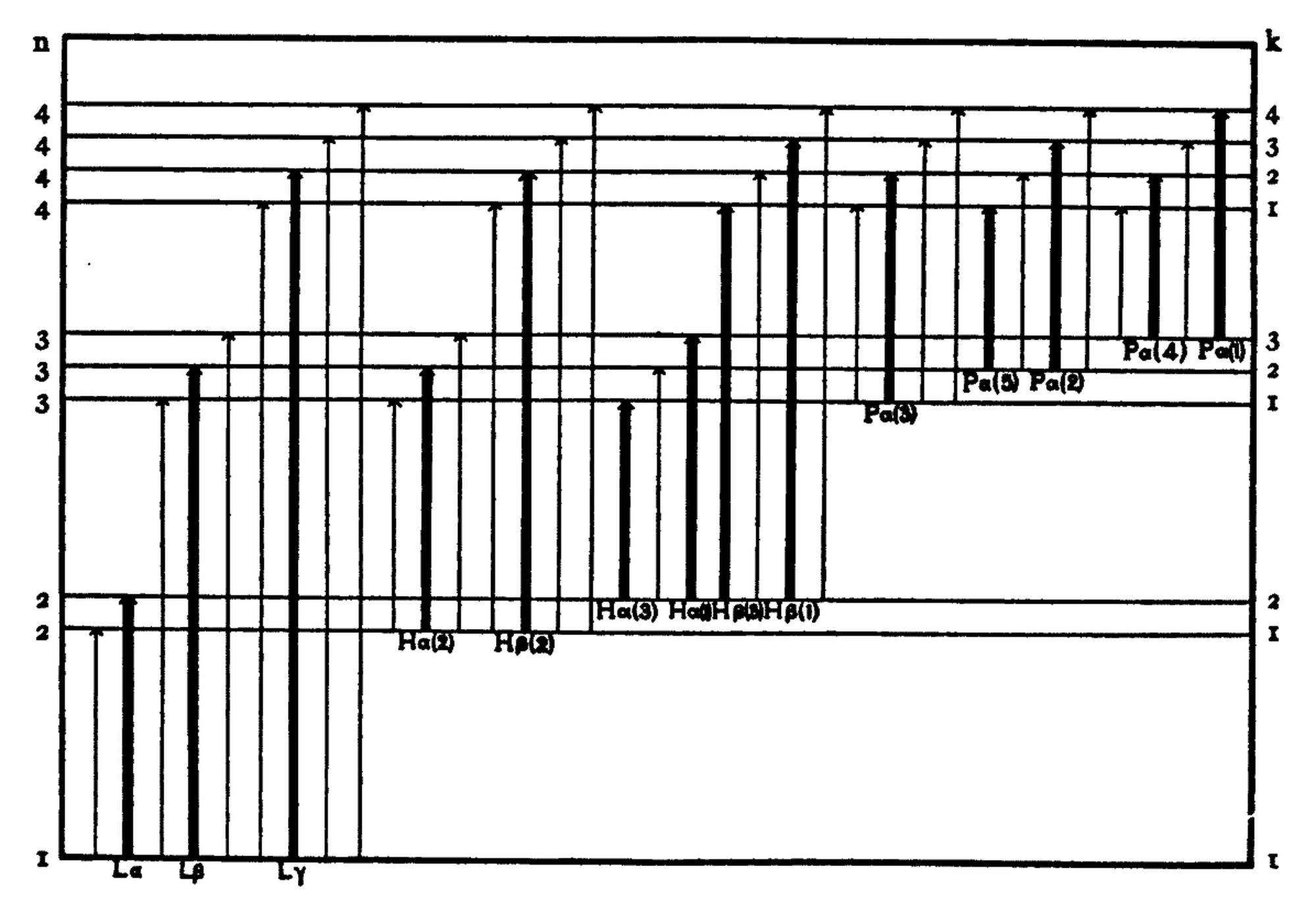
Figure 3
Energy levels for the hydrogen atom. Horizontal lines represent diagrammatically the levels of energy corresponding to all the possible electron orbits up to and including those of total quantum number four. Total quantum numbers are indicated on the left margin, azimuthal quantum numbers on the right margin. Transitions are only possible between orbits which differ by ±1 in azimuthal quantum number. All such possible transitions are indicated in the diagram by heavy lines. “Forbidden jumps,” for which the difference in azimuthal quantum number is zero or greater than 1, are indicated by light lines. This diagram embodies the same relations as Figure 2, the levels representing the various orbits in that figure.
Effectively, the ionized atom may be regarded as a new atom altogether.
It reproduces the spectrum of the atom of preceding atomic number,
in cases which have been fully investigated, with great fidelity,
excepting that the Rydberg constant in the series formula is multiplied
by four. For the twice and thrice ionized atoms the same is true, the
Rydberg constant being multiplied by nine and by sixteen in the two
cases. It is scarcely necessary to mention the beautiful confirmation
of the theory that has been furnished by the analyses[9][10] of the
spectra of Na, Mg, and Mg+, Al, Al+, and Al++, and Si, Si+, Si++,
and Si+++. The attribution of the Pickering series (first observed
in the spectrum of Puppis) to ionized helium was the first
established example of the displacement rule, and constituted one
of the earliest triumphs of the Bohr theory.[11] The detection and
resolution of the alternate components of that series, which fall very
near to the Balmer lines of hydrogen in the spectra of the hottest
stars, and the consequent derivation of the Rydberg constant for
helium,[12] represents an astrophysical contribution to pure physics
which is of the highest importance.
IONIZATION AND EXCITATION
The ionization potential of an atom is the energy in volts that is required in order to remove the outermost electron to infinity. The excitation potential corresponding to any particular spectral series is the energy in volts that must be imparted to the atom in the normal state in order that there may be an electron in a suitable electron orbit for the absorption or emission of that series. Several different excitation potentials are usually associated with one atom. The ionization potential and the excitation potentials are collectively termed the critical potentials.
From the astrophysical point of view, ionization and excitation [Pg 15] potentials are important as forming the basic data for the Saha theory of thermal ionization, with which the greater part of this work is concerned. A list of the ionization potentials hitherto determined is therefore reproduced in the following table. The first two columns contain the values obtained by the physical and spectroscopic methods, respectively. The third column contains “astrophysical estimates,” which are inserted here to make the table more complete. The derivation of the astrophysical values will be discussed[13] in Chapter XI. Physical values result from the direct application of electrical potentials to the element in question, and spectroscopic values are derived from the values of the optical terms. (See Appendix.)
| Atomic Number |
Element | Ionization potential | Reference | ||
|---|---|---|---|---|---|
| Physical | Spectroscopic | Astrophysical | |||
| 1 | H | 14.4, 13.3 | 13.54 | 1, 2, 3 | |
| 2 | He | 25.4 | 24.47 | 5, 4 | |
| He+ | 54.3 | 54.18 | 3, 5 | ||
| 3 | Li | 5.37 | 3 | ||
| Li+ | 40 | 6 | |||
| 4 | Be | 9.6 | 7 | ||
| 5 | B | 8.3 | 7 | ||
| B+ | 19.0 | 7 | |||
| 6 | C+ | 24.3 | 8 | ||
| C++ | 45 | 9, 12 | |||
| 7 | N | 16.9 | 10 | ||
| N+ | 24 | 9, 12 | |||
| N++ | 45 | 9, 12 | |||
| 8 | O | 15.5 | 13.56 | 3, 11 | |
| O+ | 32 | 9, 12 | |||
| O++ | 50 | 45 | 12 | ||
| 10 | Ne | 16.7 | 13 | ||
| 11 | Na | 5.13 | 5.12 | 14, 3 | |
| Na+ | 30-35 | 15 | |||
| 12 | Mg | 7.75 | 7.61 | 16, 3 | |
| Mg+ | 14.97 | 3 | |||
| 13 | Al | 5.96 | 3 | ||
| Al+ | 18.18 | 17 | |||
| Al++ | 28.32 | 17 | |||
| 14 | Si | 10.6 | 8.5 | 18, 19 | |
| Si+ | 16.27 | 18 | |||
| Si++ | 31.66 | 18 | |||
| Si+++ | 44.95 | 8.5 | 18 | ||
| 15 | P | 13.3, 10.3 | 20, 21 | ||
| P++ | 29.8 | 7 | |||
| P+++ | 45.3 | 7 | |||
| 16 | S | 12.2 | 10.31 | 20, 12 | |
| S+ | 20 | 9, 12 | |||
| S++ | 32 | 9, 12 | |||
| S+++ | 46.8 | 7 | |||
| 17 | Cl | 8.2 | 13 | ||
| 18 | A | 15.1 | 22 | ||
| A+ | 33, 34, 41.5 | 23, 22, 24 | |||
| 19 | K | 4.1 | 4.32 | 14, 3 | |
| K+ | 20-23 | 14 | |||
| 20 | Ca | 6.09 | 3 | ||
| Ca+ | 11.82 | 3 | |||
| 21 | Sc | 6-9 | 25 | ||
| Sc+ | 12.5 | 19 | |||
| 22 | Ti | 6.5 | 26 | ||
| Ti+ | 12.5 | 19 | |||
| 23 | V | 6-9 | 25 | ||
| 24 | Cr | 6.7 | 3 | ||
| 25 | Mn | 7.41 | 35 | ||
| 26 | Fe | 5.9, 8.15 | 7.5 | 28, 29, 19 | |
| Fe | 13 | 19 | |||
| 27 | Co | 6-9 | 25 | ||
| 28 | Ni | 6-9 | 25 | ||
| 29 | Cu | 7.69 | 3 | ||
| 30 | Zn | 9.35 | 3 | ||
| Zn+ | 19.59 | 7 | |||
| 31 | Ga | 5.97 | 3 | ||
| 33 | As | 11.5 | 30 | ||
| 34 | Se | 12-13, 11.7 | 31, 32 | ||
| 35 | Br | 1.00 | 13 | ||
| 36 | Kr | 14.5 | 33 | ||
| 37 | Rb | 4.1 | 4.16 | 34, 3 [Pg 16] | |
| 38 | Sr | 5.67 | 3 | ||
| Sr+ | 10.98 | 3 | |||
| 42 | Mo | 7.1, 7.35 | 35, 36 | ||
| 47 | Ag | 7.54 | 3 | ||
| 48 | Cd | 8.95 | 3 | ||
| Cd+ | 18.48 | 7 | |||
| 49 | In | 5.75 | 37 | ||
| 51 | Sb | 8.5 ± 1.0 | 26 | ||
| 53 | I | 10.1, 8.0 | 38, 39 | ||
| 56 | Ba | 5.19 | 3 | ||
| Ba+ | 9.96 | 3 | |||
| 80 | Hg | 10.4 | 40 | ||
| 81 | Tl | 6.94 | 41 | ||
| 82 | Pb | 7.93 | 7.38 | 42 | |
| 83 | Bi | 8.0 | 30 | ||
| Bi+ | 14.0 | 30 [Pg 17] | |||
1 Horton and Davies, Proc. Roy. Soc., 97A, 1, 1920.
2 Mohler and Foote, J. Op. Soc. Am., 4, 49, 1920.
3 A. Fowler, Report on Series in Line Spectra, 1922.
4 Lyman, Phys. Rev., 21, 202, 1923.
5 Horton and Davies, Proc. Roy. Soc., 95A, 408, 1919.
6 Mohler, Science, 58, 468, 1923.
7 D. R. Hartree, unpub.
8 A. Fowler, Proc. Roy. Soc., 105A, 299, 1924.
9 Payne, H. C. 256, 1924.
10 Brandt, Zeit. f. Phys., 8, 32, 1921.
11 Hopfield, Nature, 112, 437, 1923.
12 R. H. Fowler and Milne, M. N. R. A. S., 84, 499, 1924.
13 Horton and Davies, Proc. Roy. Soc., 98A, 121, 1920.
14 Tate and Foote, Phil. Mag., 36, 64, 1918.
15 Foote, Meggers, and Mohler, Ap. J., 55, 145, 1922.
16 Foote and Mohler, Phil. Mag., 37, 33, 1919.
17 Paschen, An. d. Phys., 71, 151 and 537, 1923.
18 A. Fowler, Bakerian Lecture, 1924.
19 Menzel, H. C. 258, 1924.
20 Mohler and Foote, Phys. Rev., 15, 321, 1920.
21 Duffendack and Huthsteiner, Amer. Phys. Soc., 1924.
22 Horton and Davies, Proc. Roy. Soc., 102A, 131, 1922.
23 Shaver, Trans. Roy. Soc. Can., 16, 135, 1922.
24 Smyth and Compton, Amer. Phys. Soc., 1925.
25 Russell, Ap. J., 55, 119, 1922.
26 Kiess and Kiess, J. Op. Soc. Am., 8, 609, 1924.
27 Catalan, Phil. Trans., 223A, 1922.
28 Sommerfeld, Physica, 4, 115, 1924.
29 Gieseler and Grotrian, Zeit. f. Phys., 25, 165, 1924.
30 Ruark, Mohler, Foote, and Chenault, Nature, 112, 831, 1923.
31 Foote and Mohler, The Origin of Spectra, 67, 1922.
32 Udden, Phys. Rev., 18, 385, 1921.
33 Sponer, Zeit. f. Phys., 18, 249, 1923.
34 Foote, Rognley and Mohler, Phys. Rev., 13, 61, 1919.
35 Catalan, C. R., 176, 1063, 1923.
36 Kiess, Bur. Stan. Sci. Pap. 474, 113, 1923.
37 McLennan, Br. A. Rep., 25, 1923.
38 Foote and Mohler, The Origin of Spectra, 67, 1922.
39 Smyth and Compton, Phys. Rev., 16, 502, 1920.
40 Eldridge, Phys. Rev., 20, 456, 1922.
41 Mohler and Ruark, J. Op. Soc. Am., 7, 819, 1923.
42 Grotrian, Zeit. f. Phys., 18, 169, 1923.
[Pg 18]
By the use of one or other of the available methods, the data for neutral atoms are complete as far as atomic number 38, with the exception of carbon (6), fluorine (9) and germanium (32). The data for ionized atoms are also increasing, at the present time, in a very gratifying manner. The “hot spark” investigations of Millikan and Bowen,[14] which permit the estimation of the fifth and sixth ionization potentials of certain light atoms, are not included in the table. Under the conditions hitherto investigated in the stellar atmosphere, ionization corresponding to a potential of about fifty volts is the highest encountered, and accordingly ionization potentials that greatly exceed this value have no place in the present tabulation of astrophysically useful data. A knowledge of the higher critical potentials[15] is, however, of great interest in connection with the theoretical problems of the far interior of the star.
There are conspicuous gaps in the table, and it is to be feared that many of them are likely to remain unfilled. The spectra of the neutral atoms of carbon, phosphorus, and nitrogen have hitherto defied analysis, and our knowledge of the corresponding ionization potentials must therefore depend on physical methods. For carbon, silicon, and similar refractory materials, such methods are difficult of application; the same applies to the metals. It is therefore probable that the ionization potentials of the neutral atoms of several of the lighter elements, of the platinum metals, and of the rare earths, will remain unknown or uncertain for some time to come. None of the atoms thus omitted is of immediate astrophysical importance.
As shown in the table, the values for the ionized and doubly ionized light atoms O+, O++, C++, N++, S+, and S++ are deduced only astrophysically. It may be hoped that the spectra of these atoms will soon be arranged in series, so that an accurate value of the ionization potential may be available, in place of the approximate one deduced from the stellar evidence, for the corresponding absorption lines are of importance in the spectra of the hotter stars.
[Pg 19]
The spectroscopic ionization potentials have an advantage over the
physical values, in that the corresponding state of the atom is
known with certainty, whereas physical methods can in general only
detect some critical potential, without assigning it definitely
to a particular transition. For example, it seems likely that in some
cases the first ionization, whether caused by incident radiation or
by electron impacts, corresponds to the loss of an electron by the
molecule:
where
represents the atom, and
the electron. The effect of
increased excitation would then be the decomposition
The first reaction would produce the ionized molecule, and the second
would produce the ionized and neutral atoms simultaneously. It
might thus happen that the
spectrum could appear without the
previous appearance of the
spectrum, since all of the element was
present in the form
before ionization.
The above is only a simple illustrative example of the possible complexity in the physical determination of ionization potentials. The interpretation of four successive critical potentials for hydrogen has been discussed by Franck, Knipping and Krüger,[16] while eight have been detected by Horton and Davies[17] for the same element. Similarly Smyth[18] discusses four critical voltages for nitrogen. No explicit attempt has yet been made to use these facts for the interpretation of astrophysical data, but they may account for the unexplained absence of some neutral elements from the cooler stars. The absence is generally to be attributed, as will be shown in Chapter V, to the non-occurrence of suitable lines in the part of the spectrum usually examined. But [Pg 20] it is possible that the persistence of the molecule has a definite significance in the case of nitrogen, where the ionization potential is as high as 16.9 volts.
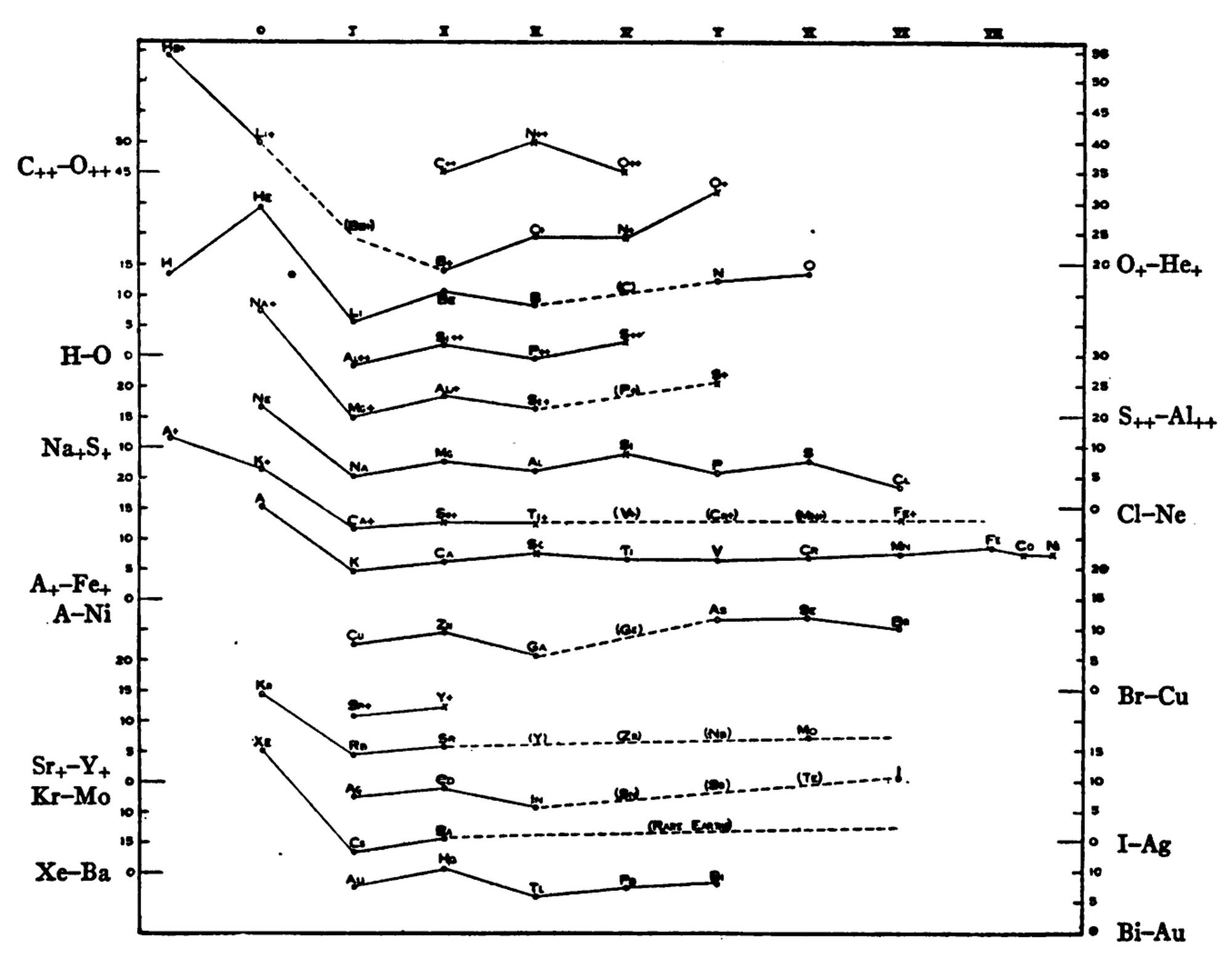
Figure 4
Relation between ionization potential and position in the periodic system. Ordinates are ionization potentials in volts, on the equal but shifted scales indicated alternately on left and right margins. Abscissae are columns of the periodic table. Physical determinations of ionization potential are indicated by open circles; dots give spectroscopic determinations, and crosses denote astrophysical estimates. Conjectural portions of the curve are indicated by broken lines, and atoms of unknown ionization potential are enclosed in parentheses.
The increasing completeness of the table of ionization potentials suggests a re-examination of the relation recently traced by the writer[19] between ionization potential and atomic number. The original diagram, in which columns of the periodic table are treated as abscissae, and the ordinates are ionization potentials on equal but shifted scales, so that analogous elements fall one below another, is here reproduced, with the addition of data more recently obtained.
[Pg 21]
The Displacement Rule of Kossell and Sommerfeld leads us to expect a pronounced similarity between the line drawn in the diagram from the point representing one element to that representing the next, and the corresponding line for the ionized atoms of the same elements, the latter being shifted one place to the left for each electron removed. The points for once and twice ionized atoms are inserted into the diagram on this principle, and the parallelism is found to exist. The regularities of the diagram and their possible significance (such, for example, as the pairing of the valency electrons, the second being harder to remove than the first) were discussed in the original paper. All the more recent data appear to confirm the conclusion there set forth, that the relation between ionization potential and atomic number is very closely the same in each period.
DURATION OF ATOMIC STATES
In addition to the critical potentials, which give a measure of the ease with which an atom is excited or ionized, astrophysical theory requires an estimate of the readiness with which an atom recovers after excitation or ionization. It appears probable that this factor, like the critical potentials, is independent of external conditions, and depends upon something that is intrinsic in the atomic structure. The “life” of the atom has been extensively investigated in the laboratory, and has been shown to be a small fraction of a second in duration. Probably this subject of “atomic lives” is still in an initial stage, and the accuracy of the results and the range of elements discussed will be greatly increased in the near future. A summary of the material obtained up to the present time is contained in the following table. Successive columns contain the atom discussed, the deduced atomic life in seconds, the authority, and the reference.
The data are practically confined to hydrogen and mercury, and for
both these elements the atomic life appears to be of the order
[Pg 22]
.
Astrophysical estimates of the life of the excited calcium atom
have been made by Milne,[20] who derives values of the order
. This is so near to the
values obtained in the laboratory that it seems permissible, in
the absence of further precise data, to assume an atomic life of
, as a working hypothesis,
for all atoms. The same value is unlikely to obtain for all atoms; in
particular it may be expected to differ for atoms in different states
of ionization. But here astrophysics must be entirely dependent on
further laboratory work for the determination of a quantity that is of
fundamental importance.
| Atom | Life | Authority | Reference |
|---|---|---|---|
| Wien | An. d. Phys., 60, 597, 1919 | ||
| Ibid. | Ibid. | ||
| Ibid. | Ibid. | ||
| Ibid. | Ibid. | ||
| Dempster | Phys. Rev., 15, 138, 1920 | ||
| Wood | Proc. Roy. Soc., 99A, 362, 1921 | ||
| Franck and Grotian | Zeit. f. Phys., 4, 89, 1921 | ||
| Mie | An. d. Phys., 66, 237, 1921 | ||
| Wien | An. d. Phys., 66, 232, 1921 | ||
| Ibid. | Ibid. | ||
| Ibid. | An. d. Phys., 73, 483, 1924 | ||
| Ibid. | Ibid. | ||
| Ibid. | Ibid. | ||
| Ibid. | Ibid. | ||
| Turner | Phys. Rev., 23, 464, 1924 | ||
| Webb | Phys. Rev., 21, 464, 1923 |
RELATIVE PROBABILITIES OF ATOMIC STATES
The relative intensities of lines in a spectrum must depend fundamentally upon the relative tendencies of the atom to be in the corresponding states. To a subject which, like astrophysics, depends [Pg 23] for its data largely upon the relative intensities of spectral lines, the theory of the relative probabilities of atomic states is of extreme importance. The question is obviously destined to become an important branch of spectrum theory. It has been discussed, from various aspects, by Füchtbauer and Hoffmann,[21] Einstein,[22] Füchtbauer,[23] Kramers,[24] Coster,[25] Fermi,[26] and Sommerfeld.[27] The comparison with observation has been made, up to the present, only for a few elements. The relative intensities of the fine-structure components of the Balmer series of hydrogen were examined by Sommerfeld,[28] and exhaustive work with the calcium spectrum has recently been carried out by Dorgelo.[29] The astrophysical application of the data bearing on relative intensities of lines in the spectrum of one and the same atom, while an essential branch of the subject, is a refinement which belongs to the future rather than to the present.
EFFECT ON THE SPECTRUM OF CONDITIONS AT THE SOURCE
(a) Temperature Class.—It is found experimentally that the relative intensities of the lines in the spectrum of a substance are altered when the temperature is changed. Some lines, notably the ultimate lines mentioned in a previous paragraph, predominate at low temperature. Other lines, which are weak under these conditions, become stronger if the temperature is raised, and lines which are the characteristic feature of the spectrum at the highest temperatures that can be attained in the furnace are often imperceptible at the outset. The effects are more conspicuous, and have been most widely studied, in the spectra of the metals, which are rich in lines and are amenable to furnace conditions. The results of such experiments, which [Pg 24] are chiefly the work of A. S. King, are expressed by the assignment of a “temperature class,” ranging from I to V, to each line; Class I represents the lines characteristic of the lowest temperatures, and Class V denotes the lines that require the greatest stimulation.
The temperature class of a line is intimately connected with the amount of energy required to excite the line. It may, indeed, be used as a rough criterion of excitation potential, high temperature class indicating high excitation energy. The temperature class is therefore useful in assigning series relations to unclassified lines, and is of value to the astrophysicist chiefly in this capacity of a classification criterion. King’s work on silicon shows, for instance, that 3906 is of Class II, and is therefore not an ultimate line—a fact which has considerable significance in studying the astrophysical behavior of the line.
The correlation of temperature class with excitation potential receives an immediate explanation in terms of the theory of thermal ionization. It furnishes a useful laboratory corroboration of the theory by showing that the thermal excitation of successive lines, with rising excitation potential, takes place in qualitative agreement with prediction.
The appended list shows the atoms for which the spectra have been analyzed by King on the basis of temperature class:
| Element | Reference | Element | Reference |
|---|---|---|---|
| Iron | Mt. W. Contr. 66, 1912 | Calcium | Mt. W. Contr. 150, 1918 |
| Titanium | Mt. W. Contr. 76, 1914 | Strontium | Ibid. |
| Vanadium | Mt. W. Contr. 94, 1914 | Barium | Ibid. |
| Chromium | Ibid. | Magnesium | Ibid. |
| Cobalt | Mt. W. Contr. 108, 1915 | Manganese | Mt. W. Contr. 198, 1920 |
| Nickel | Ibid. | Silicon | Pub. A. S. P., 22, 106, 1921 |
(b) Pressure.—In the laboratory the observed effects of pressure[30] are a widening and shifting of the lines in the spectrum—effects which differ in magnitude and direction for different lines. The phenomena are well marked under pressures of several atmospheres.
[Pg 25]
Recent developments of astrophysics, such as are summarized in Chapter III and Chapter IX, have shown that the pressures in stellar atmospheres are normally of the order of a hundred dynes per square centimeter, or less. At such pressures no appreciable pressure shifts will occur, and indeed one of the most direct methods by which these exceedingly low pressures in reversing layers have been established[31] is based on the absence of appreciable pressure effects.
(c) Zeemann Effect.—The magnetic resolution of spectral lines into polarized components[32] has, as yet, for the astrophysicist, chiefly a value as a criterion for classifying spectra. In the field of solar physics proper, a direct study of the Zeemann effect has led to important results.[33] The present study is not, however, explicitly concerned with the sun, except in comparing solar features with similar features that can also be examined in the stars.
The investigations of Landé on term structure and Zeemann effect[34] for multiplets have shown how the Zeemann pattern formed by the components into which a line is magnetically resolved can be related to the series attribution of the line. This provides a method of classifying spectra which are rich in multiplets, and which have previously defied analysis. The indirect astrophysical value of the Zeemann effect is, therefore, very great.
(d) Stark Effect.—The effect of an electric field in resolving spectral lines into polarized components was first pointed out by Stark[35] for hydrogen and helium. Several other investigators have since studied the effect for these two elements,[36] and for [Pg 26] various metals.[37][38] Unlike the temperature and magnetic effects, the Stark effect has not been used as a criterion for the series relations of unclassified lines.
The Stark effect has not been detected in the solar spectrum, presumably because the concentration of free electrons prevents the formation of large electrostatic fields.
Several investigators, however, have contemplated in the Stark effect a possible factor influencing the stellar spectrum.[39][40] It does not seem unlikely that nuclear fields could operate as a sensible general electrostatic field at the photospheric level, thus producing a widening and winging of certain lines. The question has been numerically discussed by Hulburt,[41] and Russell and Stewart,[42] in an examination of Hulburt’s work, concluded that the Stark effect might possibly make some contribution (probably not a preponderant one) to the observed widths of lines in the solar spectrum. The question is not definitely settled, but it appears well to keep so important a possibility in mind.
[1] International Atomic Weights, 1917.
[2] Aston, Isotopes, 1922; Phil. Mag., 47, 385, 1924; Nature, 113, 192, 856, 1924; Ibid., 114, 273, 716, 1924. Products of radioactive disintegration are omitted.
[3] Clarke and Washington, Proc. N. Ac. Sci., 8, 108, 1922.
[4] Bohr, Naturwiss., 11, 619, 1923.
[5] Sommerfeld, Atombau und Spektrallinien, 3d. edition, 286, 1922.
[6] A. Fowler, Proc. Roy. Soc., 105A, 299, 1924.
[7] Sommerfeld, Atombau und Spektrallinien, 3d edition, 457, 1922.
[8] Meggers, Kiess, and Walters, J. Op. Soc. Am., 9, 355, 1924.
[9] A. Fowler, Report on Series in Line Spectra, 1922; Bakerian Lecture, 1924.
[10] Paschen, An. d. Phys., 71, 151, 1923.
[11] Sommerfeld, Atombau und Spektrallinien, 3d. edition, 255, 1922; A. Fowler, Proc. Roy. Soc., 90A, 426, 1913; Paschen, An. d. Phys., 50, 901, 1919.
[12] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 348, 1922.
[14] Millikan and Bowen, Phys. Rev., 23, 1, 1924; Nature, 114, 380, 1924.
[15] Hartree, Proc. Camb. Phil. Soc., 22, 464, 1924; Thomas, Phys. Rev., 25, 322, 1925.
[16] Verh. d. Deutsch. Phys. Ges., 21, 728, 1919.
[17] Phil. Mag., 46, 872, 1923.
[18] Proc. Roy. Soc., 103A, 121, 1923.
[19] Proc. N. Ac. Sci., 10, 322, 1924.
[20] Proc. Phys. Soc. Lond., 36, 94, 1924.
[21] An. d. Phys., 43, 96, 1914.
[22] Phys. Zeit., 18, 121, 1917.
[23] Phys. Zeit., 21, 322, 1922.
[24] Proc. Copenhagen Ac., 1919.
[25] Physica, 4, 337, 1924.
[26] Physica, 4, 340, 1924.
[27] Zeit. f. Tech. Phys., 5, 2, 1925.
[28] Atombau und Spektrallinien, 3d edition, 588, 1922.
[29] Physica, 3, 188, 1923; Zeit. f. Phys., 13, 206, 1923; ibid., 22, 270, 1924; Dissertation, Utrecht, 1924; Physica, 5, 27, 1925.
[30] King, Mt. W. Contr. 53, 1911; ibid., 60, 1912.
[31] St. John and Babcock, Ap. J., 60, 32, 1924.
[32] Zeemann, Researches in Magneto-Optics, 1911.
[33] Hale, Mt. W. Contr. 30, 1908.
[34] Landé, Zeit. f. Phys., 15, 189, 1923.
[35] Stark, Elektrische Spektralanalyse Chemischer Atome, 1914.
[36] Merton, Proc. Roy. Soc., 92A, 322, 1915; ibid., 95A, 33, 1919.
[37] Anderson, Mt. W. Contr. 134, 1917.
[38] Takamine, Mt. W. Contr. 169, 1919.
[39] Evershed, Observatory, 45, 166, 1922; ibid., 45, 296, 1922.
[40] Lindemann, Observatory, 45, 167, 1922.
[41] Hulburt, Ap. J., 59, 177, 1924.
[42] Russell and Stewart, Ap. J., 59, 197, 1924.
[Pg 27]
IT is well to distinguish the different meanings that are to be associated with the term “stellar temperature.” The observed energy distribution in the spectrum, combined with the theory of black-body radiation, lead to a quantity known as the “effective temperature” of the star. This is the temperature of a hypothetical black body, the spectrum of which would have the observed energy distribution of the star in question. It has often been emphasized that the effective temperature is merely a label, for it is not the actual temperature of any specific portion of the star. Presumably the temperature of a star falls off, from the center outwards, according to the laws expressed by the theory of radiative equilibrium, and though it might thus be possible to specify, on certain assumptions, the depth in a star at which the effective temperature coincides with the actual temperature, no observational significance could attach to the information.
The theory of radiative equilibrium[43] enables us to specify the temperature gradient, and in particular to determine the central temperature, the effective temperature, and the boundary temperature, corresponding to a given energy output. These three quantities are essentially arbitrary, and the second is the only one susceptible of direct measurement, while none of them represents the actual temperature of any assignable region. In order to clarify ideas it is useful to regard the effective temperature as representing roughly the temperature of the photosphere, that is, of the region in the star that gives rise to the approximately black continuous background of the spectrum. It must, however, be remembered that “the theory provides a definite relation between temperature and optical depth, involving only one constant, the effective temperature. Suppose now ... [Pg 28] we arbitrarily select a certain temperature, and name it the photospheric temperature, and name the unknown depth at which it occurs the photospheric depth; this depth will be described by some unknown transmission coefficient, to be determined. If, taking account of absorption and emission, we proceed to calculate the transmission coefficient ... we shall simply recover the optical depth predicted by Schwarzschild’s theory.” (Milne.)[44] No method of measuring the effective temperatures of the stars by comparing their energy spectrum with that of a black body can remove the arbitrariness of the quantity thus measured.
The theory of thermal ionization permits estimates to be made of the temperatures in the reversing layers of stars. These temperatures refer to the average level at which are situated the absorbing atoms corresponding to the lines used. The differences of effective level[45] for different atoms render these “ionization temperatures” difficult to define consistently, but they represent actual temperatures of assignable regions in the star, and the extent of their agreement with the temperatures derived from the distribution of energy in the continuous spectrum is a matter of extreme interest. The material and theory from which the ionization temperatures are derived is the subject matter of Chapters VI to IX. The temperature scale used in calibration and in the discussion of the theory of thermal ionization is the scale derived from the measured effective temperatures.
The derivation of a definitive scale of effective temperatures from the numerous available observations is probably impossible at the present time. The methods employed differ widely, and the conditions for accurate intercomparison cannot be regarded as fully established. The material at present available, however, permits some general conclusions, and as the needs of astrophysics demand a working temperature scale, such conclusions are summarized in the present chapter.
[Pg 29]
In the discussion of the material a difficulty immediately arises. The scale to be derived must be based entirely, in the present stage of the observations, upon the apparently brighter stars, and it is notorious that they are not homogeneous in absolute magnitude. Theory predicts[46] that absolutely bright stars will have a lower effective temperature than stars of low luminosity belonging to the same spectral class, and this prediction is, on the whole, verified by observation. The material must therefore be selected on the basis of luminosity if a standard temperature scale is to be formed, and probably the temperature scale to be aimed at should refer to stars of some one absolute magnitude adopted as standard. Theoretically, standard mass might be preferable to standard luminosity, but, in the present state of the subject, so few masses are known that such a system would not be practicable. The ideal of referring to standard absolute magnitude was not attained by the earlier temperature scales, which were apparently based upon averages for all the available brighter stars.
The more comprehensive data for the study of the stellar temperature scale are the spectrophotometric measures of Wilsing and Scheiner,[47] of Wilsing,[48] of E. S. King,[49] and of Rosenberg.[50] The temperature scales derived by Wilsing and by Rosenberg differ by a linear factor; Rosenberg assigns higher temperatures to the hotter stars, and lower temperatures to the cooler stars. These temperature scales, and their intercomparison, have been very fully discussed by Brill,[51] who reduces all the measures to the scale given by Wilsing, and gives, for the principal Draper classes, the following comparative table for the corrected mean effective temperatures on the absolute centigrade scale.
In addition to the comprehensive data just quoted, there have been [Pg 30] numerous determinations of the temperatures of individual bright stars, chiefly by Abbot,[52] Coblentz,[53] Sampson,[54] and H. H. Plaskett.[55] In the main these values confirm the scale given in Table V, but sometimes considerable differences occur in the values given for individual stars by different investigators. At the same time, each observer is usually reasonably self-consistent, and the deviations must therefore be ascribed to differences of method. Some of the results are reproduced, for illustration, in Table VI.
| Class | Wilsing | Rosenberg | E.S. King Color Temperature |
E.S. King Total Radiation |
|---|---|---|---|---|
| 12300° | 30000° | 22700° | 22700° | |
| 11450 | 18000 | 15200 | 14900 | |
| 10250 | 1200 | 11600 | 11300 | |
| 9000 | 9000 | 8800 | 8600 | |
| 7950 | 7850 | 7900 | 7700 | |
| 6880 | 6930 | 7000 | 6800 | |
| 5980 | 6000 | 6040 | 5870 | |
| 5250 | 5200 | 5090 | 4950 | |
| 4570 | 4570 | 4570 | 4440 | |
| 3860 | 3840 | 3640 | 3550 | |
| 3550 | 3580 | 3430 | 3340 |
It is seen that the effective temperatures of individual hotter
stars vary widely among themselves. This is largely a result of the
difficulty of making the appropriate correction for atmospheric
extinction. It must, then, be supposed that the temperatures derived by
spectrophotometric methods are not trustworthy for stars hotter than
Class . The values determined by the earlier observers for the
and
classes are almost certainly too low. Rosenberg’s value
of 30,000° for
is, however, most probably too high, as will be
inferred later from the ionization temperature scale.
For the cooler stars small discrepancies also occur among the different observers. In the writer’s opinion, the lowest estimates for the [Pg 31] temperatures of the cooler stars are probably nearest to the truth.
| Star | Abott Radiometric |
Coblentz Thermoelectric |
Plaskett Wedge Method |
Sampson Photoelectric |
|
|---|---|---|---|---|---|
| Ori( |
13000° | 25000° | |||
| Cas( |
15000° | 30000 | |||
| Per( |
15000 | 14000 | |||
| Ori( |
16000° | 10000 | 14800 | ||
| Lyr( |
14000 | 8000 | 11600 | ||
| 11000 | 12800 | ||||
| ( |
Cyg( |
9000 | 9000 | 10900 | |
| Aql( |
8000 | ||||
| Cas( |
9000 | 10700 | |||
| 6000 | 8300 | ||||
| Aur( |
5800 | 6000 | 5500-6000 | 5500 * | |
| 4000 | 4200 | ||||
| Gem( |
5500 | 5000-5500 | 4200 | ||
| Tau( |
3000 | 3500 | 3400 | ||
| Ori( |
2600 | 3000 | 3400 | ||
| Peg( |
2850 | 3200 | |||
* Temperature assumed in calibration of scale.
It was mentioned at the outset that dwarf stars appear to be at a higher temperature than giants of the same spectral class. The following table summarizes the differences in temperature, as compiled by Seares.[56]
| Class | Effective Temperature | |
|---|---|---|
| Giant | Dwarf | |
| 6080° | 6080° | |
| 5300 | 5770 | |
| 4610 | 5500 | |
| 3860 | 4880 | |
| 3270 | 4120 | |
| 3080 | 3330 | |
[Pg 32]
A more detailed list of giant and dwarf temperatures was compiled
in 1922 by Hertzsprung[57] from all the material then available.
The tabulation that follows contains his values for
(the “reciprocal temperature,” where
is 14,600), and the
corresponding absolute temperature, in degrees centigrade.
| Mt. W. Class | Temperature Giant |
Temperature Dwarf |
||
|---|---|---|---|---|
| 2.00 | 7300° | |||
| 2.16 | 6770 | |||
| 2.08 | 6990 | |||
| 2.26 | 6460 | |||
| 2.30 | 6350 | |||
| 2.11 | 6920 | |||
| 2.30 | 6350 | |||
| 2.29 | 6370 | |||
| 2.34 | 6240 | |||
| 2.36 | 6190 | |||
| 2.48 | 5880 | |||
| 2.30 | 2.51 | 6340° | 5810 | |
| 2.45 | 5970 | |||
| 2.71 | 5100 | |||
| 2.83 | 2.62 | 5170 | 5580 | |
| 2.92 | 2.68 | 5020 | 5440 | |
| 2.92 | 2.64 | 5020 | 5530 | |
| 3.15 | 4730 | |||
| 3.09 | 4820 | |||
| 3.15 | 4730 | |||
| 3.25 | 2.76 | 4480 | 5300 | |
| 3.20 | 4560 | |||
| 3.29 | 4430 | |||
| 3.39 | 3.03 | 4300 | 4840 | |
| 3.48 | 3.11 | 4180 | 4700 | |
| 3.50 | 3.05 | 4160 | 4790 | |
| 3.54 | 4130 | |||
| 3.83 | 3810 | |||
| 3.86 | 3870 | |||
| 4.14 | 3530 | |||
| 4.33 | 3370 | |||
| 4.36 | 3350 | |||
| 4.35 | 3360 | |||
| 4.49 | 3250 | |||
| 4.45 | 3280 | |||
| 3.93 | 3720 |
[Pg 33]
The difference in temperature between giant and dwarf stars of the same spectral class is clearly shown in the foregoing tables. The relation of absolute magnitude to effective temperature within a given class must be regarded as definitely established by observation.
The temperatures for the cooler giant stars in both these lists are
somewhat lower than those given for the corresponding classes in Table V.
The temperature of , for instance, is placed nearer to 4000°
than to 4500°. The fact that the sun, a typical
dwarf, has an
effective temperature of 5600° seems to favor these lower values.
| Class | Temperature | Class | Temperature |
|---|---|---|---|
| 3000° | 9000° | ||
| 3000 | 10000 | ||
| 3500 | 13500 | ||
| 4000 | 15000 | ||
| 5000 | 17000 | ||
| 5600 | 18000 | ||
| 7000 | 20000 | ||
| 7500 | 25000 | ||
| 8400 | 35000 |
In concluding the summary of stellar temperatures, the ionization temperature scale is given in the foregoing table. The discussion on which the table is based is contained in Chapters VI to IX, and it is merely placed here for comparison with the preceding tabulations.
[43] Eddington, Zeit. f. Phys., 7, 351, 1921.
[44] Phil. Trans., 223A, 201, 1922.
[47] Wilsing and Scheiner, Pots. Pub., 24, No. 74, 1919.
[48] Pots. Pub., 24, No. 76, 1920.
[49] H. A., 76, 107, 1916.
[50] A.N., 193, 356, 1912.
[51] A. N., 218, 210, 1923; ibid., 219, 22 and 354, 1923; Die Strahlung der Sterne, Berlin, 1924.
[52] Rep., Smithsonian Ap. Obs., 1924.
[53] Pop. Ast., 21, 105, 1923.
[54] M. N. R. A. S., 85, 212, 1925.
[55] Pub. Dom. Ap. Obs., 2, 12, 1923.
[56] Ap. J., 55, 202, 1922.
[57] Lei. An., 14, 1, 1922.
[Pg 34]
THE theory of thermal ionization enables us to make an analysis of the spectrum of the stellar reversing layer by predicting the number of atoms of any given kind that will be effective in absorbing light from the interior of the star, under given conditions, and by comparing the predicted values with the observed intensities of the corresponding absorption lines. The results depend partly on definite physical constants associated with the atoms—the ionization and excitation potentials, and the arrangement of the electrons around the nucleus. The temperature and pressure of the region in which the atom is situated are also required before the theory can be applied. The scale of stellar temperatures was discussed in the preceding chapter, and the present chapter is devoted to a synopsis of the modern views as to pressures in the reversing layer.
Strictly speaking, we cannot refer to “the pressure in the reversing layer,” for, like the temperature, the pressure has a gradient throughout the star. This gradient, as derived from the theory of radiative equilibrium,[58] is steep in the far interior of the star, but towards the outside the rapid fall of pressure begins to decrease, and changes somewhat abruptly to a very small gradient in the photospheric region, where radiation pressure and gravitation are of the same order of magnitude. Outside this layer of transition between the region dominated by radiation pressure and the region dominated by gravitation, the pressure gradient is very shallow, and decreases until, in the tenuous outer regions of the star, there is no appreciable pressure gradient, and atoms are practically floating freely.
[Pg 35]
The outermost regions of the atmosphere, at these exceedingly low pressures, make little or no contribution to the ordinary stellar spectrum; they can only be studied in the high-level chromosphere by means of the flash spectrum obtained at a total eclipse of the sun. The spectra that are ordinarily examined are from a region that is at an appreciable depth within the star—the depth from which the light of each individual wave-length can penetrate. The “layer” of which we can obtain a spectrum is therefore not at the same depth for all frequencies; it is most deep-seated in regions of continuous background, and nearest to the surface of the star at the centers of strong absorption lines. The pressures from which the different parts of the spectrum originate differ in the same way, and the idea of “pressure in the reversing layer” is not an easy one to define significantly.
For theoretical purposes it is usual to deal with the pressure at
a given “optical depth” (a measure of the amount of absorbing
matter traversed by the radiation in coming from the level
considered). The optical depth is connected with the density
, the mass coefficient of absorption for unit density,
,
and the vertical depth,
, in the star, by the relation[59]
The density gradient is thus eliminated. The optical depth is
furthermore related to the pressure
by the relations
where
is the value of gravity at the point in question, and
whence
In considering the stellar atmosphere we are dealing with a layer
so near the surface that the value of g involved is effectively the
“surface gravity” for the star. If is constant, a condition
[Pg 36]
probably approximately fulfilled,[60] the pressure at constant optical
depth is then directly proportional to the surface gravity, which
varies as the product of the mean density and the radius of the star.
Some idea of the range in pressure with which we shall be concerned in
the stellar atmosphere can therefore be obtained from stars of known
mean density and radius.
The data for eight such stars, all of the second type, are contained in Table X, which is adapted from tabulations given by Shapley.[61] Successive columns contain the name of the star, the spectral class, the mean densities of the two components in terms of the solar density, the hypothetical radii of the two components (on the assumption of solar mass) in terms of the sun’s radius, and the product of mean density and radius for each component.
| Star | Class | Mean density | Radius | Product | ||||
|---|---|---|---|---|---|---|---|---|
| SX | Cas | 0.0004 | 0.0002 | 15.3 | 18.6 | 0.006 | 0.004 | |
| RX | Cas | 0.0005 | 0.0004 | 14.3 | 14.3 | 0.007 | 0.006 | |
| RZ | Oph | 0.001 | 0.00003 | 10.1 | 33.5 | 0.010 | 0.001 | |
| RT | Lac | 0.0013 | 0.010 | 4.6 | 4.6 | 0.059 | 0.046 | |
| W | Cru | 0.00002 | 0.000025 | 94 | 36 | 0.00019 | 0.0009 | |
| U | Peg | 0.83 | 0.67 | 1.2 | 1.2 | 1.0 | 0.8 | |
| W | G | 1.8 | 1.8 | 0.9 | 0.9 | 1.6 | 1.6 | |
| Sun | 1.0 | 1.0 | 1.0 | |||||
In mean density these stars display a range of , while the
range in surface gravity is
, illustrating the significant fact
that the mean density varies far more widely than the surface gravity.
The latter quantity is the important one in determining the pressure
that may be assumed to exist in the reversing layer. If the masses of
the very luminous stars of low mean density, such as W Crucis, exceed
the solar mass, as they most probably do, the hypothetical radii are
[Pg 37]
increased, and the range in surface gravity becomes even smaller than
before.
The data for stars of known mean density and radius permit the
estimation of the range in surface gravity, and hence of the range
in pressure, encountered in the reversing layer. In the absence of
knowledge of the appropriate optical depth, however, the actual
pressure cannot be deduced from such considerations, and recourse
must be made to more indirect methods. The present view is based upon
a number of considerations, none of which would alone be of great
weight. All of the conclusions, taken together, however, indicate
that the upper limit of the pressure for the region in which the
Fraunhofer lines originate is of the order of
.
Attention was first called to the probability of an extremely low pressure in the reversing layer by R. H. Fowler and Milne,[62] in advancing the form of ionization theory which is to be analyzed in later chapters. The conclusion that the pressure in the reversing layer is exceedingly low was a direct outcome of their discussion, and they mentioned that the results from other methods converged in the same direction.
Russell and Stewart,[63] in a specific discussion of the pressures
at the surface of the sun, have established beyond question, and on
quite other grounds, that the pressure for the solar reversing layer
is indeed of the order suggested by Fowler and Milne. The value
need then no longer be
regarded as a result of the Fowler-Milne theory, and may be used
without redundancy in deriving a stellar temperature scale from that
theory.
METHODS OF ESTIMATING REVERSING LAYER PRESSURES
Russell and Stewart examined the evidence for reversing layer pressures derived from the following sources: (a) Shifts of spectral lines due to pressure, (b) Sharpness of lines, (c) Widths of lines, (d) Flash spectrum, (e) Equilibrium of outer layers, (g) Ionization and chemical equilibrium in the solar [Pg 38] atmosphere. In addition to these we have (f) the observed limit of the Balmer series in the hotter stars, where the hydrogen lines are at or near their maximum. These sources of evidence will now be briefly discussed.
(a) Shifts of Spectral Lines.—It was at one time supposed that displacements of spectral lines, corresponding to pressures of several atmospheres, could be found in stellar spectra. More recent work,[64] however, has shown conclusively that the pressure shifts that occur are so small that it is impossible to estimate a pressure from them with any approach to accuracy. The estimated pressures are of the same order as their probable errors. This being so, the most that can be expected of the method based upon pressure effects is a demonstration of whether or no the pressure exceeds 0.1 atmosphere, and this question has now been satisfactorily answered in the negative.
[Pg 39]
(b) Sharpness of lines.—The occurrence, as sharp distinct
lines in the spectra of the stellar atmosphere, of lines that are
diffuse in the laboratory at atmospheric pressure, and only become
sharp when the pressure is very much reduced, indicates that the
pressure in the reversing layer must be extremely low. The mere
existence of distinct hydrogen lines points to a pressure of less
than half an atmosphere, as was shown by Evershed,[65] and the lines
4111, 4097, 3912 of chromium,[66] 3421, 3183 of barium,[67] and 4355,
4108, 3972 of calcium,[68] which are sharp and distinct in the solar
spectrum, but which only lose their diffuseness in the laboratory
under vacuum conditions, indicates pressures probably far lower than
0.1 atmospheres. The lines of doubly ionized nitrogen, which are seen
as sharp clear absorption lines in the early stars and the cooler
stars,[69] are also somewhat hazy under even the finest laboratory
conditions,[70] and probably arise in regions of very low pressure in
the stellar atmosphere.
(c) Widths of lines.—The width of an absorption line, produced
by “Rayleigh Scattering” close to resonance conditions, is given by
Stewart[71] as
where
is the observed width of the line,
the
wave-length expressed in the same units, and
the number of
molecules per square centimeter column in the line of sight.
It is unfortunate that the widths of Fraunhofer lines are hard to
measure and difficult to interpret. Results obtained from objective
prism spectra will probably differ from those derived with the aid of
a slit spectrograph, and moreover, in estimating a line with wings it
is hard to judge what should be regarded as the “true” line width.
Russell and Stewart[72] estimate for the
lines in the solar spectrum. Then, on the
assumption that the reversing layer has a thickness of a hundred
kilometers, the partial pressure of neutral sodium in the reversing
layer, as derived by Russell and Stewart from the formula just quoted,
is of the order
. At
the solar temperature, 5600°, about 99 per cent of the sodium present
is in the ionized condition,[73] and thus the total partial pressure
of sodium atoms may be of the order
.
If it be assumed that sodium constitutes about 5 per cent of the total
material present, the total pressure thus derived is of the
order
.
[Pg 40]
The lines are of course the ultimate lines of neutral sodium.
It will be shown[74] in Chapter IX that the partial electron pressure
in the region from which ultimate lines originate is probably between
at maximum. When 99 per cent of the atoms are ionized, the
pressure rises by a factor of about 100, and the corresponding
partial electron pressure becomes between
.
As the total pressure is probably, at the solar temperature, about
twice the partial electron pressure, the total pressure should be nearer
to
.
The total pressure derived in Chapter IX is the pressure corresponding
to the median frequency of the sodium atoms that send out light to
the exterior—it may be regarded as the average pressure for the
visible sodium. The total pressure derived from the line width, on
the other hand, is the pressure at the bottom of the layer of visible
sodium, and might therefore be expected slightly to exceed the average
pressure for the visible sodium atoms. The difference encountered,
partial electron pressure, the total pressure should be nearer to
for the average
pressure, and partial electron pressure, the total pressure should be
nearer to
for the total
absorption pressure, is in the direction that would be anticipated,
although it is larger than might have been expected. Neither value
is, however, of very high accuracy, and probably the agreement can be
regarded as quite satisfactory.
If the same formula be applied to the hydrogen lines, which may have a width[75] of the order of 5Å, high values for the partial pressure of hydrogen are obtained. The behavior of hydrogen in the spectra of the cooler stars,[76] and the abnormally high abundance[77] derived for it in Chapter XIII, suggest that here, again, a definite abnormality of the behavior of hydrogen is involved.
(d) Flash Spectrum.—It was pointed out by Russell and
Stewart[78] that the density in the region that gives the flash
spectrum must be exceedingly low. If this were not the case, the
intensity of the scattered sunlight would be great enough, as
compared to the flash itself, to register on the plate as continuous
background in the time required to photograph the flash. The pressure
thus estimated, from the minimum amount of material required to give
scattered sunlight strong enough to be registered, is less than
.
(e) Radiative Equilibrium of the Outer Layers.—At the edge of a star, where radiation pressure and gravitation no longer balance, and in consequence the existence of temperature and pressure gradients, [Pg 41] such as we observe in the reversing layer, becomes possible, the equations given by Eddington[79] for the equilibrium of the interior no longer hold. The outer layers fall off more steeply than the equations predict, and in consequence it is not possible to use the equations in deriving values for the pressure or density corresponding to a layer near the boundary at a given temperature. It is certain, however, that the density deduced from the equations will be far too high, and so the predicted density at a given temperature may be used to indicate that the pressures at the boundary of a giant star are indeed very low.
The following table is adapted from the one given by Eddington for the
relation between distance, , from the center, density
, and
temperature
, for a typical giant star of Class
, effective
temperature 6500°. The distance from the center is expressed in terms
of the solar radius, the density in grams per cubic centimeter, and
the temperature in absolute units. The last entry in the first column
represents the total radius of the star.
| |
|
|
|
|
|
|---|---|---|---|---|---|
| 0 | 0.1085 | 6,590,000° | 4 | 0.0010 | 1,380,000° |
| 1 | 0.0678 | 5,640,000 | 5 | 0.00015 | 730,000 |
| 2 | 0.0215 | 3,840,000 | 6 | 0.0000093 | 290,000 |
| 3 | 0.0050 | 2,370,000 | 6.9 | 0.000000 | ...... |
At a depth where the temperature is 290,000°, ten times the temperature
in the reversing layer of any known star, the density given is about
. An
atmosphere a hundred kilometers in thickness (the supposed approximate
depth of the reversing layer) and of this density would contain only
a hundred grams per square centimeter of surface. In order to bring
the density into harmony with the densities derived for the reversing
layer it is necessary to suppose that the value[80] of
falls to 0.4
per cent of its value at 290,000° as the temperature falls, from
[Pg 42]
290,000° to 29,000°, to 10 per cent of its value. The fall of density
displayed in the table appears to be rapid enough to warrant this
supposition; and in any case, as was pointed out earlier, the actual
fall is probably greater than the formula predicts. The general theory
of stellar equilibrium is, then, consistent with very low pressures in
the reversing layer. More than this cannot be said, as the formulae are
not directly applicable.
(f) Observed Limit of the Balmer Series.—The earlier members of
the Balmer series of hydrogen are produced by the transfer of electrons
from 2-quantum orbits to 3-quantum orbits (), 4-quantum
orbits (
), and so forth. The later members of the series
are associated with orbits of higher and higher quantum numbers. The
major axis of the orbit varies as the square of the quantum number, and
therefore a hydrogen atom which is producing, say,
, is
effectively much larger than one which is giving rise to
.
As was early suggested by Bohr,[81] the production of the higher
members of the series must depend upon the possibility of existence of
the corresponding outer orbits. As a preliminary assumption it appears
probable that the existence of the larger orbits will depend on the
proximity of neighboring atoms, and hence on the pressure.
The theoretical questions involved are very complex, and the present discussion is merely tentative. When the idea that the maximum number of lines that could be produced was a function of the pressure was first set forth, the available laboratory evidence appeared all to be in its favor. The maximum number of Balmer lines that had been produced in the vacuum tube was five, while it was well known that over twenty could be traced in absorption in some stellar atmospheres. Since that time, however, the work of R. W. Wood[82] has produced forty-seven lines of the Balmer absorption series of sodium in the laboratory at considerable pressures, and evidently the simple theory, relying on the mutual distances of the atoms to determine the number of lines that [Pg 43] can be produced, cannot be applied in this case. The matter has been discussed by Franck,[83] who points out that the outermost effective orbit in the sodium atom that gives the forty-seventh line must embrace large numbers of other atoms. He suggests that collisions are chiefly responsible for the production of the absorption lines.
Even though the simple theory is inapplicable to the laboratory
conditions, it is not necessarily invalid in the stellar atmosphere,
where conditions are far more simple, and where, in particular, the
effects of collisions are negligible. There appears, moreover, to be
a distinct observational correlation between the pressure and the
number of observable hydrogen lines. The importance of the wave-length
of the beginning of the continuous absorption, which lies just to the
red of the last Balmer line observed, and extends toward the violet,
was first indicated by Wright,[84] who recorded that the absorption
head was farther to the red in Lyrae than in
Cygni. This fact is obviously reflated to the difference in pressure
in the atmospheres of the two stars, one of which is a normal
star,
while the other is a super-giant. The observational and theoretical
importance of the question has also been discussed by Saha,[85] and by
Nicholson.[86]
The observational data in the hands of the writers just quoted were
very meagre, and the present writer and Miss Howe[87] have recently
attempted to obtain information on the number of observed Balmer
lines in a large number of stars, and to examine the correlation with
absolute magnitude. A distinct correlation is found between the number
of lines observed and the reduced proper motion, which is chosen as the
best available criterion of absolute magnitude for the numerous stars
involved (Class brighter than the fifth magnitude). It therefore
appears that the pressure, and hence the proximity of the atoms, has
some influence upon the possibility of the production of a line. The
[Pg 44]
application of Bohr’s original suggestion is hence of considerable
interest, and the resulting pressures may profitably be compared with
the pressures otherwise derived for the reversing layer.
The maximum number of lines seen, while quite consistent for plates
made with the same dispersion, is somewhat increased when the
dispersion is made much greater. The number of lines seen in the
spectra of various stars with strong hydrogen lines, made with a
dispersion of about 40 mm. between and
,
varies between thirteen and twenty. The corresponding pressures,
derived from Bohr’s estimate that a pressure of about 0.02 mm. would be
required for the production of thirty-three Balmer lines, and
on the assumption that the pressure varies as the sixth power
of the quantum number, lie between
and
.
These pressures are of course to be regarded as upper limits, for it
is possible to miss several lines at the violet end of the series, and
Wright, with larger dispersion, does indeed record twenty-four Balmer
lines in
Cygni; on the other hand it is not likely that the
estimated number will exceed the actual number of lines.
The pressures in the reversing layer, as derived from the observed limit of the Balmer series, are then of the same order as the pressures derived by the other methods outlined above. This is of especial interest because the method, if applicable, is a direct one, and gives results for individual stars, whereas all the other methods, excepting the one based on pressure shifts, are essentially indirect.
(g) Ionization and Chemical Equilibrium.—The evidence adduced by Russell and Stewart[88] has been greatly amplified by Fowler and Milne,[89] and by the data bearing on their theory which were subsequently published by the writer[90] and by Menzel.[91] It is not intended to present the evidence from ionization theory here in support of the low pressures inferred by the other methods for [Pg 45] the reversing layer. The pressure derived in the present chapter, and considered as independently established, will be used in Chapters VII ff. to derive a stellar temperature scale, for the reversing layer, from the line-intensity data presented.
SUMMARY
The following tabulation contains a synopsis of the reversing layer pressures derived by the methods that have been outlined.
The extreme tenuity of the stellar atmosphere appears to be
unquestionably established by the data set forth above, and a maximum
effective pressure of
may therefore be assumed in a discussion of the spectra of reversing
layers.
| Pressure Shifts | less than |
| Line Sharpness | less than |
| Line Width | |
| Flash Spectrum | |
| Radiative Equilibrium | order of |
| Limit of Balmer Series | |
| (Ionization | |
[58] Eddington, Zeit. f. Phys., 7, 731, 1921.
[59] Pannekoek, B. A. N., 19, 1922.
[60] Milne, Phil. Mag., 47, 217, 1924.
[61] Ap. J., 42, 271, 1915; Princeton Contr. No. 3, 82, 1915.
[62] M. N. R. A. S., 83, 403, 1923.
[63] Ap. J., 59, 197, 1924.
[64] St. John and Babcock, Ap. J., 60, 32, 1924.
[65] M. N. R. A. S., 82, 394, 1922.
[66] King, Ap. J., 41, 110, 1915.
[67] King, Ap. J., 48, 32, 1918.
[68] Saunders, quoted by Russell and Stewart, Ap. J., 59, 197, 1924.
[69] Payne, H. C. 256, 1924.
[70] A. Fowler, M. N. R. A. S., 80, 692, 1920.
[71] Stewart, Ap. J., in press.
[72] Ap. J., 59, 197, 1924.
[75] Shapley, H. B. 805, 1924.
[78] Ap. J., 59, 197, 1924.
[79] Eddington, Zeit. f. Phys., 7, 371, 1921.
[80] Russell and Stewart (loc. cit.) show that there are about 0.4 grams of matter above the photosphere per square centimeter of surface.
[81] Phil. Mag., 26, 9, 1913.
[82] Phil. Mag., 37, 456, 1919.
[83] Zeit. f. Phys., 1, 1, 1920.
[84] Wright, Nature, 109, 810, 1920.
[85] Saha, Nature, 114, 155, 1924.
[86] Nicholson, M. N. R. A. S., 85, 253, 1925.
[87] Unpublished.
[88] Ap. J., 59, 197, 1924.
[89] M. N. R. A. S., 83, 403, 1923; 84, 499, 1924.
[90] H. C. 256, 1924.
[91] H. C. 258, 1924.
[Pg 46]
THE spectrum of a laboratory source offers a somewhat inadequate comparison with the spectrum of a star. Matter can be studied terrestrially in small quantities only, and when a laboratory source is used in obtaining a spectrum, all the contributing material is collected into a very small region. With the stellar source it is quite otherwise. An enormous mass of matter, spread over a very large region, gives rise to the spectrum, and probably widely different physical conditions prevail at the origin of light of different wave-lengths. The present chapter contains a brief survey of the chief components which go to make up the stellar spectrum.
The spectrum of a star nearly always consists of a continuous background, in which the energy distribution corresponds more or less to that of a black body, and of absorption and emission lines and bands. The observed stellar spectrum is the integrated contribution from all parts of the disc, the unlined portion representing radiation that passes undisturbed from the photosphere through the reversing layer, and the light within any individual absorption line coming from the greatest depth in the reversing layer that can be penetrated by light of the corresponding frequency. This depth, which is a function of the monochromatic coefficient of absorption for the wave-length considered, is negligible when compared with the radius of the star.
DESCRIPTIVE DEFINITIONS
The solar atmosphere is probably qualitatively representative of all
normal stellar atmospheres. It has been satisfactorily described
[Pg 47]
by Russell and Stewart:[92] “At the top is a deep layer, the
chromosphere, in which the gases are held up by radiation pressure,
acting on individual atoms. The pressure and density in this layer
increase slowly downwards (as gravity somewhat overbalances radiation
pressure) and the pressure at its base may be of the order of
, or 0.0001 mm. of
mercury. Below this level, gravity is predominant in the equilibrium,
and the pressure increases rapidly with depth—the temperature
remaining nearly constant, and not far from 5000°, so long as the gases
are transparent. This region is the reversing layer. When the
pressure reaches 0.01 atmosphere, the general absorption by electron
collisions begins to render the gas hazy. This opacity increases
greatly with the pressure, and the reversing layer passes, by a fairly
rapid transition, into the photosphere, which on the scale on
which we have to study it resembles an opaque mass. As soon as the
opacity becomes important the temperature rises in accordance with
the theory of radiative equilibrium developed by Schwarzschild and
Eddington. The observed effective photospheric temperature is a mean
value for the layers from which radiation escapes to us.”
[Pg 48]
The photosphere, as has been stated, is at an extremely small depth
compared with the radius of the star. Taking the sun as an example,
it is estimated by Russell and Stewart[93] that the reversing layer,
which, with the chromosphere, is responsible for all the solar
phenomena that can be spectroscopically studied, consists of about four
tenths of a gram of matter per square centimeter of surface, and is
only a few hundred kilometers in thickness. As this embraces only about
of the mass and
of the volume of the sun, it
is clear that the features that can be studied spectroscopically are
purely superficial, and that the larger aspects of stellar composition
and constitution are left essentially untouched.
THE CONTINUOUS BACKGROUND
The continuous background of the spectrum represents the photosphere—the deepest layers from which we receive light. The energy that produces it is practically the total energy output of the star. While the actual distribution of energy in the spectrum probably conforms, in general, to that of a black body, the observed distribution naturally deviates considerably. But when corrections have been applied for atmospheric absorption, the resulting energy curves so far obtained do not appear to furnish certain evidence of serious deviation from blackness, although several investigators have suggested that their measures lead to this conclusion.[94][95][96]
If it is admitted that the energy distribution in the continuous background is sensibly black, the application of the Planck and Wien formulae furnishes methods of deriving the effective temperatures of stars from the energy distribution and the position of maximum intensity, respectively. The energy curve has therefore been extensively studied, both photographically and photometrically, and our present knowledge of stellar temperatures rests primarily upon work of this nature. The solar spectrum has been the subject of exhaustive photometric researches by Abbot[97] and Wilsing,[98] and the theory of the energy distribution, and its relation to the law of darkening, have been discussed by Lindblad,[99] and by Milne.[100] In a discussion of the solar energy curve, Milne[101] shows that the continuous spectrum can be regarded as that of a black body displaced to the violet, and that the displacement can be ascribed to the distortion of a normal black body curve by the presence of strong absorption.
H. H. Plaskett,[102] in applying the wedge method of spectrophotometry [Pg 49] to the same problem, took care to measure continuous background intensities in spectral regions free from absorption lines stronger than 0 per Angstrom, as measured on Rowland’s scale of intensities. In this way he obtained a series of measures which should give a distribution sensibly free from distortion. His result for the solar temperature agrees more nearly with that derived from the solar constant than do the results of previous observers, and therefore the idea that the continuous background approximates to blackness is borne out by observations made with the proper precautions. R. H. Fowler[103] has remarked that “there is no longer any large discrepancy between the solar constant and the color temperatures, and one may hope that further more accurate work will leave them in full agreement.”
[Pg 50]
The position of maximum intensity governs the color of the star, which is quite unrelated to the colors absorbed and radiated by the atoms in the reversing layer. In some of the Wolf-Rayet stars, apparently at very high temperatures and with atmospheres under special conditions of excitation, the continuous spectrum appears extremely faint, although there seems to be no reason for supposing that this is not merely an effect of contrast with the powerful emission “bands.” The writer believes that long exposures would demonstrate the presence of continuous background for all such stars.[104] In the spectra of some gaseous nebulae, however, no continuous background has as yet been observed,[105] nor would any be expected, if our conception of the tenuity of these bodies is correct, unless they shine partly by pure reflection. (For example, the presence of some reflected starlight is inferred from the existence of a continuous background for the Orion nebula.) The transparency of gaseous nebulae to the light of stars indicates that their general opacity is extremely low, and it is this general opacity that is operative in producing the continuous background of a photosphere.
THE REVERSING LAYER
The reversing layer, comprising the layers above the photosphere, where the general opacity has greatly decreased and selective opacity begins to be appreciable, is responsible for the lines in the spectrum, which form the major part of the material of stellar spectroscopy. When the energy flowing out through the reversing layer in any specified wave-length is less than the energy in the neighboring continuous background, an absorption line is produced in the spectrum.
Roughly speaking, if an atom absorbs the whole of the light of any given frequency that reaches it from below, it will re-emit all the energy so absorbed, and will in general do so in a random direction.[106] The intensity of the absorption line so formed will then be about 50 per cent of the intensity in the neighboring continuous background. This argument is merely illustrative; it must suffice to point out that if pure selective absorption is operative the spectrum will be crossed by lines that are considerably less intense than the background. If, on the other hand, the energy leaving the atmosphere with any wave-length is greater than the energy in the neighboring continuous background, a bright line or “emission” line appears in the spectrum. Actually, of course, it is no more an emission line than is an ordinary Fraunhofer line, for the difference between stellar absorption and emission is merely a matter of contrast with the continuous background. Both kinds of line are “full of light.”
ABSORPTION LINES
The absorption lines vary greatly among themselves and from star to star, both in intensity and in general appearance. The metallic lines, more particularly those of ionized atoms, are often extremely narrow and sharp—a feature difficult to reproduce in the laboratory, and referable to the very low pressures in the stellar atmosphere.[107] Other lines, such as those of the Balmer series of hydrogen, may be [Pg 51] of considerable width, and spread out into wings that extend as much as thirty Angstrom units on each side of the center of the line. Many other lines are probably winged, but are not of sufficient strength for the feature to be seen. The form of the wings and the general shape of the line are of high significance, and should ultimately give much information bearing on the structure of the stellar atmosphere.
Although the absorption lines are commonly regarded as “dark,” the
foregoing section indicates that they should always have an appreciable
intensity even at their centers. Measures of the central intensities of
strong absorption lines have been published by various investigators,
and the results are not all in agreement. Schwarzschild[108] gives
from a single measurement of the and
lines in the solar spectrum
(center of disc) with the Hartmann microphotometer, wings ten Angstrom
units in width on either side of the line center, and a weakening of
the intensity of the light, from the continuous background to the
center of the line, of about two and a half magnitudes. Bottlinger’s
curves[109] appear to lead to considerable intensities at the centers
of the hydrogen lines in the
stars. Others have suggested that the
central intensities are considerably lower. Abbot[110] quotes estimates
ranging from one fifth to one tenth of the continuous background for
solar lines, and H. H. Plaskett[111] states that the faintest stellar
lines have about one tenth the intensity of the continuous background,
as measured by his wedge method.[112]
Determinations of central intensity by means of precise photometry
have been made by Kohlschütter[113] and by Shapley,[114] objective
prism spectra being used in both cases. Kohlschütter gives the results
of the analysis of the spectra of twenty-one stars of Classes and
[Pg 52]
by means of the Hartmann microphotometer. The darkening from the
continuous background to the center of the line is tabulated in his
paper for
,
,
,
, and
; it ranges for
from 1.14 magnitudes for a Lyrae
to 0.42 magnitudes for
Cygni. The corresponding central
intensities are 35 and 68 per cent of the intensity of the continuous
background. The method used by Shapley employed a special set of
apertures to obtain a graded series of images for a comparison of the
central intensity with that of the adjacent background. Although it
is not certain that all the very complex photographic and photometric
difficulties involved were overcome by this method, its results are
presumably entitled to greater weight than any other determinations
of central intensity hitherto made. The intensity in the hydrogen
absorption lines of Vega was ascertained to be about 25 per cent of
that of the background.
SATURATION OF ABSORPTION LINES
The discussion outlined above presupposes that the substance producing the absorption line in the reversing layer is present in quantities great enough to absorb all the light of the appropriate wave-length, subsequently re-emitting it and giving rise to an absorption line with considerable central intensity. If the atom in question is present in quantities too small for complete absorption to take place, the central intensity of the line produced will of course be higher still. Such atoms are designated “unsaturated.” Saturation has been described by Russell[115] as follows:—“For the strong lines ... the absorption in the reversing layer is so great that a large increase in the number of absorbing atoms present alters the strength of the line very little. For the weak components ... absorption under ordinary conditions is incomplete, and the strengthening (in the spectra of sunspots) is noteworthy”—an increase in the amount of available material produces an increase in the strength of the line. The strong components are [Pg 53] saturated, the weak ones are not. It should be noted that here there is an excess of atoms for the radiation. “Saturation” is used in another sense when the word is applied to the conditions at the center of a star,[116] where there is an excess of radiation for the atoms present.
EMISSION LINES
The emission lines observed in stellar spectra differ more widely among themselves than do the absorption lines, and theory has so far been less successful in suggesting the physical conditions under which they may arise.[117] The appearance of the bright-line flash spectrum of the sun, from a region that gives no appreciable continuous spectrum, is of interest in comparing emission and absorption lines. It is fairly obvious that if the source of the flash spectrum had the photosphere behind it, the bright line would appear as absorption lines—which is indeed the case when the sun is ordinarily observed. Russell assigns both the Fraunhofer lines and part of the flash spectrum to the same region, namely the upper reversing layer. The high-level flash is, of course, assigned to the lower chromosphere. The difference between absorption and narrow emission is, as was pointed out in an earlier paragraph, purely a matter of contrast. There has, however, been no satisfactory explanation of how the phenomenon displayed by an ordinary emission line can be produced—an atom that re-emits in some wave-length more light than it receives in that wave-length. Some form of “fluorescent” emission would seem to be involved, and the question is evidently an important one for spectrum theory.
The chief types of emission are found in (a) the long period
variables at maximum, (b) the emission stars, (c) the
stars, including the Wolf-Rayet stars. All these stars are apparently
very luminous.[118] Emission is also found in some late dwarfs—for
example the
and
lines are reversed in the spectrum of
[Pg 54]
61 Cygni,[119] and doubly reversed in the solar spectrum. Furthermore the
spectra of gaseous nebulae are almost entirely composed of emission
lines; and completely abnormal types of stars, with spectra partly or
wholly composed of emission lines, might also be mentioned, notably
the novae,[120]
Carinae,[121]
Merrill’s “iron star,”[122] Z
Andromedae,[123] and[124] B. D.+11°4673. The conditions under which
bright lines appear vary so widely that a single theory is manifestly
inadequate to account for the phenomenon in every case.
[92] Ap. J., 59, 197, 1924.
[93] Ibid.
[94] H. H. Plaskett, Pub. Dom. Ap. Obs., 2, 258, 1923.
[95] C. G. Abbot, Ap. J., 60, 87, 1924.
[96] Baillaud, C. R., 178, 1604, 1923.
[97] The Sun, 1911.
[98] Potsdam Pub., 66, 1913.
[99] Lindblad, Upps. Univ. Arsskr., 1, 1920.
[100] Milne, Phil. Trans., 223A, 201, 1922.
[101] Milne, M. N. R. A. S., 81, 362 and 381, 1921.
[102] H. H. Plaskett, Pub. Dom. Ap. Obs., 2, 213, 1923.
[103] Observatory, 47, 160, 1924.
[104] H. C. 263, 1924.
[105] Hubble, Mt. W. Contr. 241, 1922.
[106] Milne, M. N. R. A. S., 84, 354, 1924.
[108] Sitz. d. Pr. Ak. d. Wiss., 47, 1183, 1914.
[109] A. N., 195, 117, 1913.
[110] The Sun, 251, 1911.
[111] Pub. Dom. Ap. Obs., 1, 325, 1922.
[112] Pub. Dom. Ap. Obs., 2, 213, 1923.
[113] A. N., 220, 326, 1924.
[114] H. B. 805, 1924.
[115] Am. Ast. Soc. Rep., 190, 1923.
[116] Eddington, Ap. J., 48, 205, 1918.
[117] M. C. Johnson, M. N. R. A. S., 85, 56, 1924.
[118] Ibid.
[119] Adams and Joy, Pub. A. S. P., 36, 142, 1924.
[121] H. A., 28, 175, 1901.
[122] Pub. A. S. P. 36, 225, 1924.
[123] Br. A. Rep., 1924.
[124] A. J. Cannon, H. B. 762, 1924.
[Pg 55]
THE identification of stellar lines and bands with those observed in the laboratory has furnished a rich source of data for astrophysics. About 25 per cent of the observed solar lines are assigned to elements in Rowland’s Table of Solar Spectrum Wave-lengths. The majority of the solar lines which are still unidentified are faint. Notwithstanding practical difficulties of identification caused by blending, and the consequent uncertainty of wave-length, most of the observed lines, at least in the cooler stars, have been satisfactorily accounted for. There remain some important strong lines and bands of unknown origin, which have been usefully summarized by Baxandall.[125]
The present chapter contains a summary of the stellar occurrence and astrophysical behavior of the chief spectrum lines which are of known origin and series relations. A few other lines, such as those of C++, N++, and O+ are included, as their series relations will probably be forthcoming in the near future. The observed chemical elements are arranged in order of atomic number. At the conclusion of the chapter the elements which have not been detected in stellar spectra are enumerated. The series notation employed follows the system advocated by Russell and Saunders,[126] which appears to meet, more fully than any other, the practical needs of modern spectroscopy.
HYDROGEN (1)
Hydrogen is represented in stellar spectra by the Balmer series
(); the ultimate lines are those of the Lyman series
(
) in the far ultra-violet, and cannot therefore be
[Pg 56]
traced in the stellar spectrum. The occurrence of the secondary
spectrum of hydrogen, ascribed to the hydrogen molecule H₂, has been
suspected,[127] but not definitely established. Only one of the lines
has been recorded, and this should almost certainly be attributed[128]
to N++. The familiar Balmer series appear as emission lines in the
Wolf-Rayet stars, but normally they are absorption lines in all
succeeding classes.
The intensity of the hydrogen lines is at a maximum[129] in the
neighborhood of Class . They vary greatly in width, however,
within a given spectral class,[130] and it is difficult to find a
method of photometry applicable to the comparison of lines of very
different widths. The maximum of the Balmer lines has been placed by
Menzel[131] at
. The writer is inclined to believe that no
significant maximum can in fact be derived for the Balmer lines; beyond
, however, their intensity falls off rapidly.
It is peculiar to the Balmer series to appear in every class of the normal stellar sequence, and its lines at maximum exceed in strength the lines of every other element which appears in stellar spectra, excepting those of ionized calcium.
Although hydrogen is presumably unable to give rise to an “enhanced”
spectrum, as the atom only possesses one extra-nuclear electron, the
lines of the Balmer series share with those of neutral helium the
peculiarity of behaving like the lines of an ionized atom.[132] They
are weakened in dwarf stars, and greatly strengthened in the
cooler super-giants, such as
Orionis. The peculiarity of
the astrophysical behavior of the hydrogen atom also appears in the
impossibly high value that is assigned by ionization theory to the
relative abundance of this element.[133] An explanation, in terms
of metastability, has been suggested by Russell and Compton,[134]
but although the hypothesis appears very satisfactory in the case
[Pg 57]
of hydrogen, it is not applicable to the similar problem of helium.
Russell[135] has remarked that “there seems to be a real tendency for
lines, for which both the ionization and excitation potentials are
large, to be much stronger than the elementary theory would indicate.”
The hydrogen lines are often conspicuously winged. Measures of the width and intensity-distribution of the wings are discussed elsewhere.[136] Wings are probably not peculiar to the hydrogen lines, but the hydrogen wings can be studied because of their strength. The feature is also seen in helium, calcium and iron lines, and wings of greater or less strength are probably universal.
The width of the hydrogen lines in stars has been correlated with
absolute magnitude, and used for the estimation of luminosities.[137]
It appears, however, that the line width may not furnish an accurate
measure of absolute magnitude, although it serves to discriminate stars
having the c-character from those of smaller luminosity.[138] The
occurrence of wings seems, moreover, to be independent of line width
and of absolute magnitude.[139] These questions are connected with
the problem of classifying the
stars, and are discussed in a later
chapter.[140]
The continuous spectrum of hydrogen, beyond the limit of the Balmer series, corresponding to the continuous radiation observed in the laboratory for sodium by Wood,[141] and for helium by Lyman,[142] was first noted in stellar spectra by Sir William Huggins.[143] The beginning of the band appears just to the red of the last Balmer line observed.[144] It appears, from work in progress at the Harvard Observatory,[145] that the limit is nearer to the violet, the higher the luminosity, and in a nebular spectrum quoted by Hubble,[146] it almost coincides with the theoretical limit of the series.
[Pg 58]
The largest number of hydrogen lines recorded is thirty-five,
measured by Mitchell[147] in the flash spectrum. Thirty-three were
observed in emission by Evershed[148] in the solar chromosphere,
and Deslandres[149] traced twenty-nine in the spectrum of a bright
solar prominence. Twenty-seven Balmer lines have been observed by
Curtiss[150] in the spectrum of Tauri—the greatest number
recorded for the spectrum of a star. The number of Balmer lines
observed is related in Chapter III to the pressure in the reversing
layer.
HELIUM (2)
Helium is represented in stellar spectra by the ,
,
,
, and possibly
the
series. Lines associated with these series appear almost
simultaneously as we progress through the
star sequence, attain
a maximum[151] at
, and have disappeared[152] in normal
stars. The ultimate lines are the
series,[153] in the far
ultra-violet, and cannot be traced in the stars.
The helium lines vary much in width and definition and are often
winged. Their intensity does not certainly appear to vary with absolute
magnitude within a given spectral class, and they cannot therefore be
used in the estimation of spectroscopic parallaxes.[154] The question
of absolute magnitude effects cannot be usefully pursued in the absence
of more reliable parallaxes, for the stars, than are at present
available.
[Pg 59]
Although the lines of helium do not appear in the normal star,
they are observed in the spectrum of the super-giant
Cygni,
where the pressure is presumably exceedingly low. The
lines also appear in the flash spectrum.[155]
IONIZED HELIUM
The lines of ionized helium appear only in the hottest stars, being
peculiar to the sequence. The
lines (the “Pickering,”
or “
Puppis” series) are well marked in the hotter
stars,
although all the lines usually available are probably blended.[156]
The alternate Pickering lines are practically superposed on the
Balmer lines, and the components were separated for several stars
of Class
by H. H. Plaskett.[157] The “4686” series (
)
appears in absorption in all the so-called “absorption
stars,” and
is even faintly seen in some
stars. The line at 4686 appears
very readily as an emission line, and the wide bright “band” at this
wave-length, which is a conspicuous feature of the Wolf-Rayet stars, of
gaseous nebulae, and of certain stages of a nova, is also presumably
due to ionized helium.
LITHIUM (3)
The element lithium is represented in the sunspot spectrum by the
(ultimate) doublet at 6707, which is not, however,
strong enough to be detected in stellar spectra. Russell[158] has
called attention to the fact that this line is fainter, in the sun,
than would be anticipated from the terrestrial abundance of the
element. Compton[159] has suggested that the faintness may be ascribed
to low atomic weight, and the consequent blurring of the line by a
Doppler effect, owing to the high velocity of thermal agitation.
CARBON (6)
There is no evidence of the presence of neutral carbon in stellar atmospheres. The apparent absence of the element is partly due to the fact that the ultimate[160] line is at 2478, too far in the ultra-violet to be detected. The spectrum of neutral carbon is as yet unclassified, and other lines cannot, therefore, be sought for in the stellar spectrum. The temperature at which the element vaporizes is [Pg 60] given by Kohn and Guckel[161] as 4000°, and by Violle[162] as 3800°. The heat of vaporization has been evaluated by de Forcrand.[163] At stellar temperatures, the carbon present is probably vaporized, but possibly it is largely in combination as cyanogen or as an oxide, since spectra associated with these compounds appear in low-temperature stars.
IONIZED CARBON
Ionized carbon[164] is represented in the stellar spectrum by the
fundamental doublet (), at 4267, and by the principal
doublet (
) at 6580. The occurrence of these lines
is of great interest. The line at 4267 is found in the
stars,[165]
reaches a maximum at
, and is last seen[166] at
. It also
occurs in the spectra of some gaseous nebulae.[167] In the stellar
spectra in which it occurs, the line is sharp and clear, and, apart
from appearing as an emission line in certain stars of Class
, it has
no abnormal stellar behavior.
The principal doublet at 6580 has been said to occur in the Wolf-Rayet
spectrum,[168][169][170] and to be much stronger than the fundamental
doublet. The identification has been discussed by Wright,[171] and does
not appear to be very probable. A knowledge of the behavior of the line
at 6580 in the late and early
stars is greatly to be desired.
DOUBLY IONIZED CARBON
Merton[172] has described a spectrum, produced under conditions of high excitation, which shows several correspondences with the emission bands of the Wolf-Rayet stars. His spectrum contains the [Pg 61] fundamental and principal doublets of C+, as well as a number of other lines, which have not as yet been assigned to series. Some of these lines are probably to be referred[173] to the atom of C++, and the writer[174] considers it unnecessary to assume the occurrence of a higher degree of excitation for the Wolf-Rayet spectrum. Some of the lines which are bright in the spectra of emission-line stars have been attributed to C+++ on astrophysical grounds,[175] and also from a discussion of frequency differences.[176] The four strongest groups in Merton’s spectrum, however, consist of triplets, and this points more probably to C++, as does also the ionization potential deduced astrophysically[177] from the behavior of the only group accessible in ordinary stellar spectra. When the doublets due to C+, and the triplets already mentioned, are accounted for in Merton’s spectrum, there remain only two lines at 5696 and 5592. A line[178] with the latter wave-length is attributed by Fowler and Brooksbank[179] to O++. The evidence for stellar C+++ appears, therefore, to be inconclusive.
COMPOUNDS OF CARBON
Cyanogen. The bands headed at 3885, 4215, have been attributed [180] to the CN or the C₂N₂ radical, or to the molecule of nitrogen. The assignment to a particular atom is essentially a question for the terrestrial physicist, and to discuss it here would be out of place.[181] The bands are universally known as the “cyanogen bands,” and this designation will therefore be adopted.
The 3885 and 4215 bands are conspicuous in and
stars of low
density,[182] and furnish a valuable method for the measurement
[Pg 62]
of absolute magnitude—a method which has been used both at Mount
Wilson[183] and at Harvard.[184] The band at 3885 is largely
responsible for cutting off the ultra-violet light of the cooler
stars.[185]
Cyanogen absorption has been reported as early[186] as ,
and according to Lindblad[187] it reaches a maximum at
.
The cyanogen bands reach great intensity in the
stars, and are
indeed the most conspicuous feature of these spectra. Shane[188]
places the maximum in Class
, and is doubtless correct in so
doing. The maximum given by Lindblad refers to the series
, and the
stars are notoriously not members of that
sequence.[189] Cyanogen is also a typical constituent of the comet-head
spectrum.[190][191][192]
Carbon Oxides. The band spectrum attributed to the CO
molecule,[193][194]
is a strong feature of the spectra of and
stars.[195][196] It is also the chief component of the spectrum of the
comet tail, which has been reproduced in the laboratory, at very low
pressures, by A. Fowler.[197]
Swan Spectrum. The bands of the Swan spectrum are clearly to be assigned to some compound of carbon,[198][199] but the source is not as yet certainly established. They are characteristic of the comet head.[200] Another band, presumably to be associated with the Swan spectrum, was identified in the heads of nine comets by Baldet.[201] [Pg 63] The ordinary Swan bands are also identified in the comet tail.[202]
Hydrocarbon. The identity of the “” band with the 4314
hydrocarbon group was pointed out by Newall, Baxandall and Butler.[203]
The strength of the band is increased, in the stellar spectrum, by the
superposition of the
lines of calcium, and by the
lines of titanium, as well as other metallic lines,
but the presence of the hydrocarbon band is certain, and is of the
highest interest. The “
” band is first seen in some spectra[204] of
Class
, and it attains a maximum at
or
.
The number of carbon compounds which occur lends plausibility to the suggestion that much of the stellar carbon is in combination at temperatures below 5000°.
NITROGEN (7)
The spectrum of neutral nitrogen has not as yet been satisfactorily analyzed into series.[205] It is quite possible that the first ionization that takes place is the ionization of the molecule,[206] which is accompanied by the production of the well known band spectrum. This spectrum has not been observed in the stars; presumably it would appear at lower temperatures than those involved in the coolest spectral classes. It is, however, stated to be a conspicuous feature of the spectrum of the aurora,[207][208] and it is found in the spectrum of the comet head.[209] These occurrences seem to point to very low temperature and pressure at the source. It is possible that much of the nitrogen present in cooler stars is in combination with carbon.[210]
The green Aurora line was thought by Vegard[211] to coincide [Pg 64] with a line emitted in the laboratory by solid nitrogen. The conclusion was questioned by McLennan and Shrum,[212] who failed to produce the line under similar conditions, and subsequently found a line, of the same wave-length as the aurora line, in the spectrum of a mixture of oxygen and helium.[213] Various previous attempts to identify the aurora line with a line produced in the laboratory had failed conspicuously.[214]
IONIZED NITROGEN
The spectrum of ionized nitrogen has recently been analyzed by A.
Fowler.[215] The line which is most conspicuous in stellar spectra is
the one at 3995 (), which appears[216] at
or earlier,
reaches maximum at
, and is last seen at
. Many of the
fainter lines[217] are not observed.
DOUBLY IONIZED NITROGEN
The lines of doubly ionized nitrogen were singled out by Lockyer[218]
as showing “abnormal behavior”—they do not appear in the same
classes as the N+ line. The early work on the subject is discussed by
Baxandall.[219] The most conspicuous lines are those at 4097, 4103,
and they attain great intensity in the stars;[220] they are,
for example, very conspicuous in 29 Canis Majoris. H. H.
Plaskett[221] places the maximum of the N++ lines in the Victoria class
. They are last seen in some
stars.
[Pg 65]
The occurrence and behavior of the N+ and more especially the N++ lines in the Nova spectrum has been the subject of numerous investigations.[222][223][224][225][226][227]
OXYGEN (8)
The ultimate lines of neutral oxygen occur[228] at a wave-length of
about 1300, and accordingly cannot be observed in the spectra of
stars. It was long supposed that neutral oxygen was entirely absent,
but the triplet at 7700 is observed in the solar
spectrum,[229] is strengthened in sunspots, and is strong in the high
level chromosphere.[230] The ionization and excitation potentials
corresponding to the production of these lines are of the same order
as those for the Balmer series of hydrogen, and the astrophysical
behavior of the triplet should therefore be similar to that of the
hydrogen lines, with a maximum at or near
. Special work in the
red is, however, required to trace the behavior of the series. The
second member, the triplet at 3947, is not certainly present in the
solar spectrum, and is not recorded for any star of Class
. In the
laboratory, the second triplet is about as powerful as the first,[231]
and its apparent weakness at the theoretical maximum is difficult to
explain.
IONIZED OXYGEN
The spectrum of ionized oxygen should consist of pairs, and numerous
lines have been tabulated as belonging to this atom.[232] The lines are
found in stars, as seems first to have been noticed by Lunt.[233]
According to the present writer,[234] they are first seen at
,
although H. H. Plaskett, working with slit spectra, records[235] some
O+ lines in Class
. The maximum of the O+ lines falls between
and
, and their disappearance is mentioned[236] as a criterion
of Class
.
[Pg 66]
The lines at 4069, 4072, 4076, appear to form a triplet, but are more
probably two pairs with two of the lines coalesced. Some stronger lines
(page 207) persist in Class .
DOUBLY IONIZED OXYGEN
The spectrum of O++ has been tabulated by A. Fowler and
Brooksbank,[237] but not analyzed into series. The lines of this
atom are certainly present[238][239] in the stars of Class . The
astrophysical behavior of the lines of doubly ionized oxygen has led to
the estimation of an ionization potential,[240][241] of 45 volts for
the corresponding atom.
COMPOUNDS OF OXYGEN
Oxides.—Numerous oxides, such as carbon monoxide CO, titanium
oxide TiO₂, zirconium oxide ZrO₂, and water H₂O, are present in the
cooler stars. The metallic oxides are discussed under the corresponding
metallic element. The occurrence of steam in the spectrum of the
sunspot was announced by Cortie,[242] who supported his argument,
originally based upon the widening, over sunspots, of telluric water
vapor bands, by the observation that the presence of water vapor is
essential, in the laboratory, to the production of the spectrum of
magnesium hydride, which also occurs in the sunspot spectrum.[243] It
is possible that the formation of oxides may account for the weakness
of the spectrum of neutral oxygen in the cooler stars, but this
explanation can hardly account for the absence of the second member of
the series from the spectra of the
stars, where the
lines should have their maximum intensity.
[Pg 67]
Ozone.—The ozone bands which appear in solar and stellar
spectra have been shown by Fowler and Strutt[244] to be of telluric
origin. The maximum thermal formation of ozone occurs [245] at
and 3500°, and thus its
presence in giant
and
stars might possibly be anticipated.
SODIUM (11)
The ultimate lines () of the neutral atom of sodium
are the
lines, which lie at 5889, 5895. These are the only sodium
lines which are certainly identified in stellar spectra.[246] They are
first seen in the later
classes, and appear to be strengthened in
cool stars, in accordance with theory.
Stationary sodium lines are observed[247] in Scorpii,
Orionis, and other Class
stars.[248]
The lines are said to show an absolute magnitude effect, being
strengthened in giant stars.[249]
No lines of ionized sodium are found in stellar spectra, presumably because they all lie in the far ultra-violet.
MAGNESIUM (12)
The neutral atom of magnesium is represented in the solar spectrum by
the , the
, and the
series,
and the first triplet of the latter series constitutes the conspicuous
“b” group in the green. The “b” group and the second member of the
series, the triplet near 3800, are first seen[250] at
, have a maximum near
or
, and are still strong
in the coolest stars examined. The
series, represented
in the solar spectrum by a line at 4571, are faint ultimate lines;
the strong ultimate lines[251] are the
lines beginning at
2852, and are therefore outside the range of observed solar and stellar
spectra.
IONIZED MAGNESIUM
The ionized magnesium atom gives rise to the important combination
doublet at 4481 (). These lines appear in the
sequence,[252] reach maximum[253] at
(not at
, as stated
by several investigators), and are lost in the increasing strength of
[Pg 68]
the iron line at the same wave-length, at about
. The doublet
varies with absolute magnitude, and may be found to furnish a useful
criterion of that quantity. It has been used by H. H. Plaskett[254] in
the estimation of the temperatures of some of the stars of Class
.
COMPOUNDS OF MAGNESIUM
Magnesium hydride.—The compound magnesium hydride, MgH₂, which has been studied in the laboratory by Brooks[255] and Fowler,[256] was detected by the latter in the sunspot spectrum.[257] It is perhaps significant that the only other hydride reported in celestial spectra is that of calcium, the next heavier alkaline earth after magnesium.
ALUMINUM (13)
Neutral aluminum is represented in the solar spectrum by the
lines, the series that constitutes the ultimate
lines in the third column elements of the periodic table.[258] The
two conspicuous lines of the series in aluminum are those at 3944,
3957, and they are strengthened in cool stars,[259] in accordance
with theory. They are especially mentioned as being strong in the
spectrum[260] of 61 Cygni, as might be expected for a dwarf
star. The
series is also traced in the solar
spectrum, but is too far in the ultra-violet to be studied effectively
in the stars.
The series lines[261] of Al+ and Al++, although they might be expected
in the stars, apparently have not yet been traced in stellar
spectra.
SILICON (14)
Four stages of the silicon atom are observed in stellar spectra.
The line at 3905 is found in the coolest stars, has an observed
[Pg 69]
maximum[262] at , and disappears at about
. This line is
regarded by A. Fowler[263] as the ultimate line of the neutral atom,
and on this basis an ionization potential of 10.6 volts was assigned to
silicon. In view of the fact that the line appears to have a maximum
within the stellar sequence, and is of temperature class II, according
to King,[264] while the true ultimate line[265] of silicon is at 2881,
it seems possible that 3905 is actually a subordinate line.
IONIZED SILICON
Ionized silicon is represented by the lines 4128, 4131, which appear
at , attain maximum[266] at
, and disappear at
.
These lines are of especial interest, as they form the characteristic
feature of the “silicon stars” which occur in the early
classes.
The silicon stars are specially discussed[267]
in Chapter XII.
DOUBLY IONIZED SILICON
The lines associated with the atom Si++ which appear in stellar spectra
are the three at the wave-lengths 4552, 4568, 4574. These lines
are first seen at , have a maximum[268] between
and
, and disappear at
. Fowler[269] regards these lines as
constituting a principal triplet; it might be expected, however, that
principal lines would show a more persistent maximum.
TRIPLY IONIZED SILICON
[Pg 70]
The atom of silicon which has lost three electrons is the most highly
ionized atom of which we have certain evidence in stellar spectra. The
lines at 4089, 4096, and 4116 are strong[270] among the cooler
stars, and are last seen at Class
. The hotter
stars, such
as H.D. 165052, do not display the lines of Si+++, and probably the
intensity of the lines has fallen, owing to the temperature, which is
above that required for the maximum of these lines.
SULPHUR (16)
The spectrum of neutral sulphur which has hitherto been analyzed is chiefly in the far ultra-violet,[271] and is therefore not traceable in the sun or stars.
Two sets of sulphur lines, differing in astrophysical behavior, were
noted by Lockyer[272] at 4163, 4174, 4815, and at 4253, 4285, 4295.
These lines have been attributed by the writer,[273] and by Fowler and
Milne,[274] to S+ and S++ respectively. The S+ lines appear to be in
pairs, and the S++ lines suggest a triplet, although one of the three
lines is extremely faint in stellar spectra, and it would be expected
that the once and twice ionized spectra of sulphur would display even
and odd multiplicities respectively. The two series have maxima at
and at
, but the stellar intensities of the lines are
small. An amplification of our knowledge of stellar sulphur is greatly
to be desired.
POTASSIUM (19)
The ultimate lines[275] of potassium () are at 7664
and 7699, and have been traced in the solar spectrum, although they
are very faint. They appear to be absent from the flash spectrum.[276]
Russell[277] expresses the opinion that they persist, with rising
temperature, as far as
in the stellar sequence.
CALCIUM (20)
The element calcium is extensively represented in stellar spectra.
The ultimate line of the neutral atom is at 4227 () and
appears at
. The line increases in strength in all cooler
stars, in accordance with theory, and has a distinct variation with
[Pg 71]
absolute magnitude. The
,
and
multiplets[278] are satisfactorily identified in the solar spectrum
and can be traced with certainty in the spectra of stars cooler than
. The
,
,
, and
lines
appear to be present with the appropriate intensities in the sun, but
are too faint to be seen with small dispersion. Thus all the classified
lines of calcium which are strong in laboratory spectra have been
traced in the spectra of the sun and stars.
IONIZED CALCIUM
The and
lines of ionized calcium are seen throughout the
stellar sequence, and reach a maximum within the
type,[279] where
their intensity is greater than that attained by any other line in any
class. They vary with absolute magnitude.[280] In the sun the lines
are doubly reversed, and they are probably singly reversed[281] in
61 Cygni.
Stationary calcium lines have long been known to occur in the
spectra of certain spectroscopic binaries, having first been noticed
by Hartmann[282] for Orionis. Various “calcium cloud”
hypotheses have been advanced to account for the phenomenon. It
appears, from several considerations, notably the apparent small
oscillation of the calcium lines with the same period as the star, that
there is some physical connection between the two. Lee[283] discussed
the idea that the system of 9 Camelopardalis was surrounded
by a cloud of calcium vapor, which, as he showed, could be made to
account for the behavior of the lines of ionized calcium. The same idea
was discussed by J. S. Plaskett, who suggested that we might “assume
that the absorbing material is near to or envelopes the stars, which is
probable from its wide distribution, and in this form it combines the
two original hypotheses of interstellar and surrounding clouds.”[284]
The
lines of sodium[285]
[Pg 72]
and possibly the hydrogen lines[286]
have been added to the list of stationary lines, and Plaskett[287] has
suggested that the ultimate lines of the ionized atoms of strontium and
barium should also show the effect, which has not yet, however, been
observed.
SCANDIUM (21)
The element scandium[288] is represented in the solar spectrum
by faint lines corresponding to the multiplets ,
,
. The multiplet
may possibly be present, but the lines are very weak. The element is
not recorded in the spectra of stars; most of the lines are unsuitably
placed in the green.
IONIZED SCANDIUM
Six multiplets of ionized scandium, out of the eight tabulated by Meggers, Kiess, and Walters[289] appear in the solar spectrum, and all the corresponding lines have been traced in Rowland’s tables. The intensity of two of the lines is great enough for their behavior to be traced through the stellar sequence, and they are greatly enhanced in the spectra of the c-stars. The ultimate lines are near 3600, but in the solar spectrum they are less powerful than the lines near 3500.
Table XI on page 73 contains, in successive columns, the series relations, the wave-length as determined in the laboratory, the intensity, the temperature class, and the attribution, solar intensity, and wave-length given by Rowland, for the six multiplets which lie within the observed range of the solar spectrum. Ultimate lines are designated by an asterisk.
TITANIUM (22)
[Pg 73]
The spectrum of titanium is so rich in lines, and is so largely represented in stellar spectra, that a tabulation would occupy an undue amount of space.
| Series | Wave-Lenght | Int. | Cl. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|---|
| 3613.84 | 60 | II | -, Sc | 4 | 3613.947 | |
| 3645.31 | 30 | III | Sc?, - | 3 | 3645.475 | |
| 3630.76 | 50 | II | 4 | 3630.876 | ||
| 3666.54 | 3 | III | 1 | 3666.676 | ||
| 3651.81 | 25 | III | -, Sc | 4 | 3651.940 | |
| 3642.79 | 40 | II | Sc | 2 | 3642.912 | |
| 3572.53 | 50 | II | -, Sc | 6 | 3572.71 | |
| 3558.55 | 20 | II | (Fe | 8 | 3558.672) | |
| 3590.48 | 20 | II | 2 | 3590.609 | ||
| 3576.35 | 35 | II | -, Sc? | 3 | 3576.527 | |
| 3567.70 | 20 | II | 4 | 3567.835 | ||
| 3589.64 | 20 | II | 5 | 3589.773 | ||
| 3580.94 | 30 | II | 5 | 3581.067 | ||
| 5657.89 | 25 | V E | Y, - | 2 | 5658.09 | |
| 5684.21 | 12 | V E | 1 | 5684.415 | ||
| 5640.99 | 15 | V E | 2 | 5641.206 | ||
| 5667.16 | 9 | V E | 0 | 5667.368 | ||
| 5658.35 | 8 | V E | 0 | 5658.561 | ||
| 5669.05 | 10 | V E | 1 | 5669.258 | ||
| 4374.46 | 40 | III E | Sc, Fe? | 3 | 3374.628 | |
| 4420.66 | 2 | 00 | 4420.832 | |||
| 4354.60 | 5 | V E | 1 | 4354.776 | ||
| 4400.38 | 30 | III E | Sc | 3 | 4400.555 | |
| 4431.35 | 3 | V E | 0 | 4431.525 | ||
| 4384.80 | 6 | IV E | 0 | 4384.986 | ||
| 4415.55 | 20 | III E | 2 | 4415.722 | ||
| 4314.09 | 60 | III E | Sc | 3 | 4314.248 | |
| 4294.77 | 8 | IV E | Zr | 2 | 4294.932 | |
| 4320.73 | 50 | III E | Sc | 3 | 4320.90 | |
| 4279.95 | 1 | - | - | ---- | ||
| 4305.70 | 10 | IV E | 2 | 4305.871 | ||
| 4325.00 | 40 | III E | Sc | 4 | 4325.152 |
From an examination of Rowland’s tables of the solar spectrum, it appears that the fainter components of the multiplets invariably accompany the stronger ones, thus making the identifications certain. [Pg 74] Only the stronger components are, however, powerful enough to appear in stellar spectra, with the dispersions ordinarily used.
The following multiplets, as analyzed by Russell[290] and Kiess,[291]
are definitely present: ,
,
,
,
,
,
,
,
,
,
. Doubtfully
present are:
,
.
The maximum of these lines is difficult to determine; they are not
well placed for measurement, many of the most important are seriously
blended, and all are rather faint, even at maximum. They are first
seen[292] at Class , and their maximum appears to be[293] at
or
.
The solar intensities of the lines of both neutral and ionized titanium fall off regularly with increasing excitation potential. The subject is discussed in Chapter VII, as part of the evidence for the validity of the Saha theory.[294]
IONIZED TITANIUM
The lines of ionized titanium are about as strong in the solar spectrum
as those of the neutral atom. Many of them appear, with the lines of
the ionized iron atom, with abnormal strength in the spectra of the
c-stars.[295] The following multiplets[296] are present in the solar
spectrum: ,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
. Doubtfully present are
,
,
,
. The lines
which are especially enhanced in the c-stars are:
,
,
,
,
,
,
,
.
The lines of ionized titanium come to a maximum at about Class ,
but a significant maximum is difficult to determine, for the lines are
[Pg 75]
extremely sensitive to absolute magnitude. Menzel,[297] using
Cassiopeiae (classed by him as
) for his typical star, found a
maximum development of lines in that star. The present writer,[298]
using the wider selection of stars enumerated in the appendix,
obtains
as the maximum for Ti+. A glance at the measures[299]
will indicate that the position of the maximum is in any case very
uncertain, as the intensity does not change smoothly in going from
class to class.
COMPOUNDS OF TITANIUM
The absorption bands of titanium oxide, TiO₂, are the characteristic
flutings[300][301]
of the stars of Class , and the strength of these
bands has been proposed[302] as a criterion of class for the stars
in which they are found. It is perhaps noteworthy that titanium,
zirconium, and carbon, the only elements which give oxides in stellar
spectra (hydrogen excepted) belong to the fourth group of the periodic
system.
VANADIUM (23)
The vanadium lines are best identified by intensity from Rowland’s
table. The following multiplets[303] are present in the solar
spectrum: ,
,
,
,
,
,
. The
multiplet is well seen in
stellar spectra from
onwards, and increases in strength as
cooler stars are approached.[304] Slipher[305] called attention to
the strength in
Ceti of the vanadium group near 4400,
presumably the two multiplets
,
,
with excitation potential 0.28 volts.
[Pg 76]
IONIZED VANADIUM
Three multiplets, all far in the ultra-violet, are tabulated for
ionized vanadium by Meggers, Kiess, and Walters,[306] and two of them
are within the range of Rowland’s table. All the lines of these, the
and
multiplets, have been satisfactorily
identified with solar lines. The strength of the ultimate lines of
ionized vanadium, which occur in the multiplet last named, is a little
greater, in the solar spectrum, than that of the strongest lines of the
neutral atom, at 4379, which are also ultimate lines.
The following tabulation contains, in the same form as Table XI, the data respecting the two multiplets which are identified in the solar spectrum.
| Series | Wave-Lenght | Int. | Cl. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|---|
| 3727.348 | 20 | - | 1 | 3727.488 | ||
| 3760.230 | 5 | - | 1 | 3760.364 | ||
| 3718.163 | 3 | - | 3718.291 | |||
| 3750.873 | 15 | - | 2 | 3751.015 | ||
| 3778.359 | 3 | - | (Fe | 3 | 3778.463) | |
| 3743.63 | 3 | - | (Cr | 1 | 37243.726) | |
| 3770.976 | 10 | 2 | 3771.116 | |||
| * |
3093.10 | 40 | III Er | 3093.229 | ||
| 3121.144 | 20 | IV E | V | 4 | 3121.270 | |
| * |
3102.301 | 40 | III Er | V | 3 | 3102.404 |
| 3145.35 | - | - | 3 | 3145.484 | ||
| 3126.221 | 25 | IV E | V, Fe | 5 | 3126.319 | |
| * |
3110.710 | 30 | III Er | Ti, V | 3110.810 | |
| 3145.979 | 5 | V Er | Zr | 1 | 3146.091 | |
| 3130.270 | 25 | III E | V | 3 | 3130.380 | |
| * |
3118.382 | 30 | III Er | V | 3 | 3118.498 |
| 3145.344 | 10 | IV E | 3 | 3145.484 | ||
| 3133.336 | 20 | III E | V | 2 | 3133.449 | |
| * |
3125.286 | 40 | III Er | 5 | 3125.399 |
[Pg 77]
CHROMIUM (24)
The lines of chromium were classified by Catalan,[307] and those which
occur in the sun are comprised in the following multiplets:[308]
,
,
,
,
,
,
,
,
,
,
,
.
The ultimate lines , at 4254, 4274, 4289 increase
with advancing type.[309] The maximum for subordinate lines[310] is at
.
IONIZED CHROMIUM
Of the six multiplets of ionized chromium tabulated by Meggers, Kiess, and Walters,[311] only two are within the measured range of the solar spectrum, but every line in these two multiplets accords satisfactorily in wave-length and intensity with a line in Rowland’s table. The ultimate lines are in the neighborhood of 2800, and are therefore unattainable. The lines, and the solar intensities, are contained in the appended table.
| Series | Wave-Lenght | Int. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|
| 3328.34 | 3 | 1 | 3328.487 | ||
| 3336.33 | 5 | Cr | 2 | 3336.477 | |
| 3324.06 | 3 | 3324.19 | |||
| 3339.80 | 10 | Co, Cr | 3 | 3339.932 | |
| 3347.83 | 6 | Cr | 3 | 3347.970 | |
| 3342.58 | 10 | Cr | 3 | 3342.717 | |
| 3358.50 | 10 | Ti, Cr | 4 | 3358.649 | |
| 3368.04 | 20 | Cr, - | 3368.193 | ||
| 3132.04 | 20 | -, Cr | 4 | 3132.169 | |
| 3124.97 | 20 | Cr | 4 | 3125.109 | |
| 3147.22 | 5 | Cr | 3 | 3147.350 | |
| 3120.36 | 15 | Cr, - | 3 | 3120.481 | |
| 3136.69 | 5 | Cr, Co | 3 | 3136.822 | |
| 3159.10 | 1 | 0 | 3159.225 | ||
| 3118.65 | 10 | Cr, - | 2 | 3118.764 | |
| 3128.68 | 5 | Cr, - | 2 | 3128.819 | |
| 3145.07 | 2 | 2 | 3145.251 |
[Pg 78]
MANGANESE (25)
The lines of manganese are conspicuous in stellar spectra, and all
the classified lines[312] within the range of Rowland’s table are
found in the solar spectrum, namely the multiplets ,
,
,
,
,
,
,
,
,
. The ultimate
lines
are at 4030, and constitute a conspicuous group
in the solar spectrum. They are well seen in the cooler stars, and are
progressively strengthened with advancing type.[313] They first appear
at
. The
multiplet, at 4018, 4041, 4055,
4084, etc., has a maximum, according to Menzel,[314] at
.
IONIZED MANGANESE
Meggers, Kiess, and Walters[315] give one multiplet of ionized
manganese, and this is within the range of Rowland’s table. The
multiplet was previously picked out by Catalan[316] as being analogous
to the arc multiplet . All the lines can be
satisfactorily identified with lines in the solar spectrum, as in the
following table.
| Series | Wave-Lenght | Int. | Cl. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|---|
| 3441.999 | 9 | V | Mn | 6 | 3442.118 | |
| 3474.050 | 7 | V | Mn | 2 | 3474.197 | |
| 3460.332 | 8 | V | Mn, - | 3460.460 | ||
| 3496.815 | 4 | V | Co, Mn | 3 | 3496.952 | |
| 3482.918 | 7 | V | Mn, - | 3483.047 | ||
| 3474.13 | 6 | V | Mn | 2 | 3474.287 | |
| 3497.540 | 6 | V | Mn | 3 | 3497.668 | |
| 3488.618 | 8 | V | Mn | 4 | 3488.817 | |
| 3495.810 | 8 | V | Mn | 2 | 3495.974 |
[Pg 79]
IRON (26)
The extensive occurrence of the arc lines of iron in the stellar
spectrum is well known. The following multiplets[317] have been
traced in the solar spectrum, and the corresponding lines are also
to be traced in the spectra of the cooler stars: ,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
. The iron lines
have, in general,[318] a maximum at
, but the only ultimate
lines which are well shown in stellar spectra, the
lines near 4480, increase with advancing type to the end of the
sequence.[319]
The following lines are used as criteria of absolute magnitude by
Harper and Young:[320] 4202, 4250, 4272 (), 4072
(
), 4482 (
).
IONIZED IRON
[Pg 80]
The lines of ionized iron are strong in F stars of high luminosity, and
are especially conspicuous in the stars which have the c-character.
Menzel[321] places the maximum at , and the writer[322] finds it
at
. The following multiplets, as classified by Russell,[323]
occur in the solar spectrum:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Doubtfully present are:
,
,
. The ionized iron lines are strengthened, as are
other enhanced lines, over sunspots, and many of the fainter components
of multiplets are observed only in the spot spectrum.
COBALT (27)
The series relations for the arc spectrum of cobalt[324] have been
published by Walters. Cobalt lines are frequent in the solar spectrum,
but as the strongest of them lie near 3500, they cannot be traced in
the spectra of stars. The following multiplets are certainly identified
in the spectrum of the sun: ,
,
,
,
,
,
,
,
,
, and
. The incompletely observed
multiplet
is apparently absent from the solar spectrum.
NICKEL (28)
The series relations for nickel are as yet unpublished. The lines
appear in great numbers in the solar spectrum, but they are not strong
enough to be conspicuous in the spectra of the stars. The line 5476
appears to have a maximum at , indicating either that it is
an enhanced line of nickel, or that it is blended with the enhanced
line of some other element. The lines 5081, 4714 are strengthened in
low temperature stars, and are probably due to neutral nickel. From
the solar behavior of the lines of this element,[325] the ionization
potential seems to be of the same order as that for cobalt, probably
about 8 volts.
COPPER (29)
Copper is represented in the solar spectrum by the ultimate doublet
3273, 3247 (), which is strong. The pair 5700, 5782
(
) is probably also present. The former lines are too far
in the ultra-violet to have been studied in the stars, and the latter
are too faint.
ZINC (30)
The principal singlet is at 2138, and has therefore not
been observed in stellar spectra. The
lines at 4722,
4810, are seen in the stellar sequence, where they appear at
,
and have a maximum[326] at
.
[Pg 81]
Two unclassified lines of ionized zinc are mentioned in Fowler’s Report as lying at 5894, 6214. Neither of these lines can be traced in solar or stellar spectra.
GALLIUM (31)
The occurrence of gallium in stellar spectra is confined to the
identification of two solar lines by Hartley and Ramage.[327] The
lines in question are at 4033, 4172, and are the ultimate lines of the
element (). They are too faint to be studied in the
stars.
RUBIDIUM (37)
The ultimate lines of rubidium have been detected in the sunspot spectrum,[328] but they are not found in the spectra of the sun or stars.
STRONTIUM (38)
The element strontium is of great astrophysical importance, owing to
the use of its enhanced lines in the estimation of absolute magnitudes.
The neutral atom is represented in the sun and stars by the ultimate
line () 4607, which is first clearly seen[329] at
,
and increases progressively in strength with advancing type. It varies
with absolute magnitude, being weakened in stars of high luminosity
later than
. Estimates for the intensity of this line are
difficult with small dispersions, as it is blended in cool stars.
IONIZED STRONTIUM
Ionized strontium is represented in stellar spectra by the
and the
series. The former contains
the important absolute magnitude lines 4215, 4077, which are first seen
at about
, and reach a maximum[330] near
. They appear
to have “abnormal” intensities in certain stars,[331] and in the
stars are often the finest and sharpest lines in the spectrum. This
behavior suggests a high-level origin, but “stationary Strontium,”
[Pg 82]
although suggested by Plaskett[332] as likely to occur, has not yet
been observed.
YTTRIUM (39)
Numerous lines of yttrium[333] are found in the solar spectrum. The lines of the ionized atom are somewhat stronger than the lines of the neutral atom. The lines of the neutral element which can be identified in the solar spectrum are contained in the following table.
| Series | Wave-Lenght | Int. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|
| 3620.94 | 20 | Y? | 00 | 3621.110 | |
| 3592.91 | 10 | Y | 0 | 3593.040 | |
| 3552.69 | 3 | - | - | ||
| 4128.32 | 30 | 00 | 4128.46 | ||
| 4039.83 | 5 | Y | 00 | 4040.013 | |
| 4047.65 | 8 | Y | 4047.823 | ||
| 4102.38 | 20 | Y | 0 | 4102.541 | |
| 4167.52 | 10 | 00 | 4167.737 | ||
| 4077.39 | 20 | La, Y | 4077.498 |
The multiplets at 4174, etc., and
at 4674,
etc., and the
multiplets, do not appear in the solar
spectrum. None of the above lines is strong enough to be seen in the
spectra of the stars.
IONIZED YTTRIUM
[Pg 83]
Four of the multiplets attributed to ionized yttrium[334] are satisfactorily identified in the solar spectrum. The wave-lengths and identifications are contained in Table XVI, p. 83. The arrangement is as in Table XI.
| Series | Wave-Lenght | Int. | Attribution | Int. | Wave-Lenght |
|---|---|---|---|---|---|
| * |
3710.30 | 100 | Y | 3 | 3710.431 |
| 3832.87 | 20 | 3833.026 | |||
| * |
3774.33 | 50 | Y | 3 | 3774.473 |
| 3878.27 | 4 | 1 | 3878.334 | ||
| 3818.37 | 10 | Y | 1 | 3818.487 | |
| * |
3788.69 | 30 | 2 | 3788.839 | |
| 3600.72 | 50 | Y | 3 | 3600.880 | |
| 3548.99 | 20 | Y? | 2 | 3549.151 | |
| 3664.59 | 20 | Y | 2 | 3664.760 | |
| 3611.05 | 30 | Y, Mg? | 2 | 3611.189 | |
| 3584.51 | 10 | Y | 2 | 3584.660 | |
| 3628.70 | 10 | Y, Mg? | 2 | 3628.847 | |
| 3601.91 | 20 | Y | 1 | 3602.060 | |
| 4309.61 | 20 | 1 | 4309.792 | ||
| 4235.71 | 6 | 0 | 4235.894 | ||
| 4199.283 | 3 | 00 | 4199.434 | ||
| 4398.03 | 15 | In zircon * | 1 | 4398.178 | |
| 4358.72 | 8 | Y-Zr | 0 | 4358.879 | |
| 4422.60 | 10 | Fe, Y | 3 | 4422.741 | |
| 5087.42 | 10 | Y? | 1 | 5087.601 | |
| 4982.12 | 3 | 000 | 4982.319 | ||
| 5320.77 | 1 | - | - | ||
| 5205.71 | 10 | Y | 0 | 5205.897 | |
| 5119.10 | 3 | 00 | 5119.292 | ||
| 5289.81 | 2 | 000 | 5289.988 | ||
| 5200.41 | 8 | V | 0 | 5200.590 |
* But not Zr.
ZIRCONIUM (40)
The ultimate lines of the zirconium atom[335] are all found in the solar spectrum, far into the ultra-violet.
The bands in the spectra of stars of Class are found to correspond
with those of ZrO₂, zirconium oxide.[336] A comparison
[Pg 84]
of the furnace spectrum of zirconium oxide with that of titanium oxide, which produces
the characteristic flutings in Class
, indicates that titanium oxide
persists to lower temperatures.[337] It is of interest to note that
the only oxides, other than water, which have been detected in stellar
spectra, are those of elements in the fourth column of the periodic
table, namely carbon, titanium and zirconium. Probably this has a
chemical interpretation. The presence of silicon dioxide SiO₂ has not
been detected, although it might be anticipated.
NIOBIUM (41)
Rowland identifies some of the lines associated with niobium in the solar spectrum. The series relations are unknown, and the lines are too faint to be detected in stellar spectra.
MOLYBDENUM (42)
All the ultimate lines of molybdenum are present in the solar spectrum. They are too faint to be detected in the stars. The spectrum has been analyzed into series by Kiess,[338] and by Catalan.[339]
RUTHENIUM (44) RHODIUM (45) PALLADIUM (46)
The strongest lines in the spectra of the three lighter platinum metals are all present in the solar spectrum,[340] but are too faint to be traced in the spectra of stars. Series relations are as yet unknown. The heavier platinum metals, osmium (76), iridium (77), and platinum (78), are not certainly found in the solar spectrum.
SILVER (47)
[Pg 85]
The ultimate () lines of silver are at 3281 and 3383.
They are both faintly present in the solar spectrum. The doublet at
4669, 4476 (
) is also probably present in the spectrum
of the sun. The lines cannot be traced in stellar spectra.
TIN (50)
A line of neutral tin was reported by Lunt[341] in the spectrum of
Scorpii. Series relations are as yet unknown. In view of the
absence of identifications of related lines, the attribution cannot be
regarded as very certain. The strongest line in the spectrum of ionized
tin is stated by the same investigator to lie at 4585.80. This line is
either absent from or exceedingly weak in the solar spectrum.
BARIUM (56)
Neutral barium is not certainly present in stellar spectra. The first
two ultimate lines () fall in the red and the ultra-violet
respectively, and would therefore escape notice in the stars. No lines
of corresponding wave-length appear in Rowland’s table, but they are
found in sunspots.[342] The
groups are also absent from the
solar spectrum.
The strength of the barium lines in the sun has been thought by Russell to be abnormal, and the question has been considered by several investigators.[343][344][345]
IONIZED BARIUM
Ionized barium is represented by the lines which are
present, though weak, in the sun, and by the
lines,
which appear[346] at
, and increase in intensity for all cooler
stars. The
line is at 4555, and its behavior is
difficult to trace, as it is much blended.
THE RARE EARTHS (57-71)
The spectra of the rare earths are so rich in lines that spurious
identifications with lines in stellar spectra are often likely to
occur. Numerous attributions to lanthanum (57), cerium (58), and
[Pg 86]
neodymium (60) are given in Rowland’s table. The occurrence of some of
these elements has also been definitely established in the spectra of
certain stars. Kiess[347] has demonstrated the presence of europium
(63) and of terbium (65) in Canum Venaticorum. Numerous
lines, identified with those of rare earth elements, are reported by
Mitchell[348]in the chromospheric spectrum.
If the lines in the chromosphere and the star are indeed derived
from the rare earths, the atoms concerned must be at least singly
ionized. No series relations have as yet been published for any rare
earth element, excepting a short list of relative term values for
lanthanum.[349] From analogy with the previous long period it would
seem unlikely that the first ionization potential of these atoms can be
as great as 13 volts, the value which would be required if the lines
have a maximum intensity at
.
LEAD (82)
A single line is attributed to lead in Rowland’s table.
RADIUM (88)
Giebeler and Küstner[350] suggested the occurrence of radium lines in the chromosphere. The identification was discussed by Dyson[351] and by Mitchell.[352] In the light of later knowledge it appears improbable that an element so heavy, and terrestrially so rare,[353] would be present in the sun at sufficient heights and in great enough quantity to appear in the flash spectrum. The identification is probably to be regarded as spurious.
ELEMENTS NOT DETECTED IN STELLAR SPECTRA
The table which follows contains a list of elements which are absent, or of doubtful occurrence. The rare earths are omitted from the list.
[Pg 87]
The elements marked “doubtful” in the list are those for which coincidences with very faint solar lines occur.[354] Twelve out of the twenty-nine elements enumerated are halogens, inert gases, or metalloids, and it is significant that all the elements of these groups are absent, with the sole exception of helium.
| At. No. | Element | Remark | At. No. | Element | Remark |
|---|---|---|---|---|---|
| 4 | Beryllium | Doubtful | 53 | Iodine | Absent |
| 5 | Boron | Absent | 54 | Xenon | Absent |
| 9 | Fluorine | Absent | 73 | Tantalum | Doubtful |
| 10 | Neon | Absent | 74 | Tungsten | Doubtful |
| 15 | Phosphorus | Absent | 76 | Osmium | Doubtful |
| 17 | Chlorine | Absent | 77 | Iridium | Doubtful |
| 18 | Argon | Absent | 78 | Platinum | Doubtful |
| 32 | Germanium | Doubtful | 79 | Gold | Absent |
| 33 | Arsenic | Absent | 80 | Mercury | Doubtful |
| 34 | Selenium | Absent | 81 | Thallium | Doubtful |
| 35 | Bromine | Absent | 83 | Bismuth | Doubtful |
| 36 | Krypton | Absent | 86 | Radon | Absent |
| 49 | Indium | Doubtful | 90 | Thorium | Doubtful |
| 51 | Antimony | Absent | 92 | Uranium | Doubtful |
| 52 | Tellurium | Absent |
[125] M. N. R. A. S., 83, 166, 1923; ibid., 84, 368, 1924.
[126] Ap. J., 61, 38, 1925.
[127] Wright, Lick Pub., 13, 242, 1918.
[128] A. Fowler, M. N. R. A. S., 80, 692, 1920.
[129] H. A., 91, 7, 1918.
[130] Fairfield, H. C. 264, 1924.
[131] H. C. 258, 1924.
[132] Ibid.
[134] Nature, 114, 86, 1924.
[135] Personal letter.
[137] Mt. W. Contr. 262, 1922.
[138] Fairfield, H. C. 264, 1924.
[139] Lindblad, Ap. J., 59, 305, 1924.
[141] Ap. J., 29, 100, 1909.
[142] Ap. J., 60, 1, 1924.
[143] Atlas, p. 85, 1892.
[144] Wright, Nature, 109, 810, 1920.
[146] Pub. A. S. P., 32, 155, 1920.
[147] Mitchell, Ap. J., 38, 431, 1913.
[148] Phil. Trans., 197A, 381, 1901.
[149] C. R., 114, 578, 1892.
[150] Pub. Obs. Mich., 3, 256, 1923.
[151] Payne, H. C. 256, 1924; ibid., 263, 1924.
[152] Henry Draper Catalogue; criterion of class.
[153] Lyman, Phys. Rev., 21, 202, 1923.
[154] Payne, Nature, 113, 783, 1924.
[155] Mitchell, Ap. J., 38, 407, 1913.
[156] H. C. 263, 1924.
[157] Pub. Dom. Ap. Obs., 1, 335, 1922.
[158] Mt. W. Contr. 236, 1922.
[159] Mt. W. Contr. p. 160, 236, 1922.
[160] De Gramont, C. R., 171, 1106, 1920.
[161] Naturwiss., 12, 139, 1924.
[162] Quoted by de Forcrand.
[163] C. R., 178, 1868, 1924.
[164] A. Fowler, Proc. Roy. Soc., 105A, 299, 1924.
[165] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 351, 1922.
[166] Payne, H. C. 256, 1924.
[167] Wright, Lick Pub., 13, 193, 1918.
[168] W. W. Campbell, Ast. and Ap., 13, 448, 1894.
[169] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 287, 1924.
[170] T. R. Merton, Proc. Roy. Soc., 91A, 498, 1915.
[171] Wright, Lick Pub., 13, 193, 1918.
[172] T. R. Merton, Proc. Roy. Soc., 91A, 498, 1915.
[173] A. Fowler, Proc. Roy. Soc., 105A, 299, 1924.
[174] H. C. 263, 1924.
[175] R. H. Fowler and Milne, M. N. R. A. S., 84, 502, 1924.
[176] D. R. Hartree, Proc. Camb. Phil. Soc., 22, 409, 1924.
[177] R. H. Fowler and Milne, M. N. R. A. S., 84, 502, 1924.
[178] M. N. R. A. S., 77, 511, 1917.
[179] Wright, Lick Pub., 13, 193, 1918.
[180] Mulliken, Nature, 114, 858, 1924; Birge, Phys. Rev. 23, 294, 1924; Freundlich and Hocheim, Zeit. f. Phys., 26, 102, 1924.
[181] Kayser, Handbuch der Spektroskopie, Vol. VII, 132, 1924.
[182] Evershed, Kod. Bul. 36, 1913.
[183] Lindblad, Mt. W. Contr. 228, 1922.
[184] Shapley and Lindblad, H. C. 228, 1921.
[185] Lindblad, Mt. W. Contr. 228, 1922.
[186] Shapley, H. B. 805, 1924.
[187] Mt. W. Contr. 228, 1922.
[188] L. O. B. 329, 1919.
[189] Rufus, Pub. Obs. Mich., 3, 257, 1923.
[190] A. Fowler, M. N. R. A. S., 70, 176, 1909.
[191] Evershed, M. N. R. A. S., 68, 16, 1907.
[192] Pluvinel and Baldet, Ap. J., 34, 89, 1907.
[193] Merton and Johnson, Proc. Roy. Soc., 103A, 383, 1923.
[194] A. Fowler, M. N. R. A. S., 70, 176, 1909.
[195] Hale, Ellerman, and Parkhurst, Yerkes Pub., 2, 253, 1903.
[196] Shane, L. O. B. 329, 1919.
[197] M. N. R. A. S., 70, 176 and 484, 1909.
[198] Strutt, Proc. Phys. Soc. Lond., 23, 147, 1911.
[199] Stead, Phil. Mag., 22, 727, 1911.
[200] A. Fowler, M. N. R. A. S., 70, 176 and 484, 1909.
[201] C. R., 177, 1205, 1923.
[202] Pluvinel and Baldet, Ap. J., 34, 89, 1911.
[203] M. N. R. A. S., 76, 640, 1916.
[205] Fowler, Report on Series in Line Spectra, 164, 1922.
[206] Smyth, Proc. Roy. Soc., 103A, 121, 1923.
[207] Vegard, Videns. Skr., 1, nos. 8, 9, 10, 1923, where previous work is summarized.
[208] Vegard, Proc. Amst. Ac., 27, 1 and 2, 1924.
[209] A. Fowler, M. N. R. A. S., 70, 484, 1909.
[211] Vegard, Proc. Amst. Ac., 27, 1 and 2, 1924.
[212] Proc. Roy. Soc., 106A, 138, 1924.
[213] Nature, 115, 382, 1925.
[214] Lord Rayleigh, Proc. Roy. Soc., 100A, 367, 1921; ibid. 101A, 312, 1922.
[215] A. Fowler, Proc. Roy. Soc., 107A, 31, 1925.
[216] Payne, H. C. 256, 1924.
[217] Ruark, Mohler, Foote, and Chenault, Bur. Stan. Sci. Pap. 480, 1924.
[218] Proc. Roy. Soc., 82A, 532, 1909.
[219] Pub. Solar Phys. Comm., 1910.
[220] Payne, H. C. 256, 1924.
[221] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 356, 1922.
[222] Paddock, Pub. A. S. P., 31, 54, 1919.
[223] Plaskett, J. R. A. S. Can., 12, 350, 1918.
[224] Baxandall, Pub. A. S. P., 311 297, 1919.
[225] Wright, M. N. R. A. S., 81, 181, 1920.
[226] Ibid. Pub. A. S. P., 32, 276, 1920.
[227] Stratton, M. N. R. A. S., 79, 366, 1919.
[228] Hopfield, Ap. J., 59, 114, 1924.
[229] Runge and Paschen, Wied. An., 61, 641, 1897.
[230] Curtis and Burns, unpub.
[231] A. Fowler, Report, 167, 1922.
[232] Ibid.
[233] An. Cape Obs., 10, 5B, 1906.
[234] Payne, H. C. 256, 1924.
[235] Pub. Dom. Ap. Obs., 1, 325, 1922.
[236] Henry Draper Catalogue, H. A., 91, 1918.
[237] M. N. R. A. S., 77, 511, 1917.
[238] Wright, Lick Pub., 13, 193, 1918.
[239] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 325, 1922.
[240] Payne, H. C. 256, 1924; Proc. N. Ac. Sci., 10, 322, 1924.
[241] R. H. Fowler and Milne, M. N. R. A. S., 84, 499, 1924.
[242] Cortie, Ap. J., 28, 379, 1908.
[243] A. Fowler, M. N. R. A. S., 67, 530, 1907.
[244] Proc. Roy. Soc., 93A, 577, 1917.
[245] Riesenfeld and Beja, Medd. Vetens. Nobelinst., 6, 8, 1923.
[246] Menzel, H. C. 258, 1924.
[247] Heger, L. O. B. 326, 1918.
[248] Heger, L. O. B. 337, 1922.
[249] Luyten, Pub. A. S. P., 35, 175, 1923.
[250] Menzel, H. C. 258, 1924.
[251] de Gramont, C. R., 171, 1106, 1920.
[252] H. H. Plaskett, Pub. Som. Ap. Obs., 1, 325, 1922.
[253] Menzel, H. C. 258, 1924.
[254] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 325,1922.
[255] Proc. Roy. Soc., 80A, 218, 1907.
[256] Phil. Trans., 209A, 447, 1909.
[257] M. N. R. A. S., 67, 530, 1908.
[258] R. H. Fowler and Milne, M. N. R. A. S., 83, 403, 1923.
[259] Menzel, H. C. 258, 1924; p. 122.
[260] Adams and Joy, Pub. A. S. P., 36, 142, 1924.
[261] Paschen, An. d. Phys., 71, 151, 1923.
[262] Payne, H. C. 252, 1924.
[263] Bakerian Lecture, 1924.
[264] King, Pub. A. S. P., 33, 106, 1921.
[265] de Gramont, C. R., 171 1106, 1920.
[266] Payne, H. C. 252, 1924.
[268] Payne, H. C. 252, 1924.
[269] Bakerian Lecture, 1924.
[270] Payne, H. C. 263, 1924.
[271] Hopfield, Nature, 112, 437, 1923.
[272] Proc. Roy. Soc., 80A, 50, 1907.
[273] H. C. 256, 1924.
[274] M. N. R. A. S., 84, 499, 1924.
[275] Fowler, Report on Series in Line Spectra, 1922.
[276] Curtis and Burns, unpub.
[277] Personal letter.
[278] Russell and Saunders, Ap. J., 61, 38, 1925.
[279] Menzel, H. C. 258, 1924.
[280] Ibid.
[281] Adams and Joy, Pub. A. S. P., 36, 142, 1924.
[282] Ap. J., 19, 268, 1904.
[283] Lee, Ap. J., 37, 1, 1913.
[284] Pub. Dom. Ap. Obs., 2, 16, 1924.
[285] Heger, L. O. B. 326, 1918; ibid. 337, 1922.
[286] Rufus, J. R. A. S. Can., 14, 139, 1920.
[287] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 344, 1924.
[288] Russell, Mt. W. Contr., in press.
[289] J. Op. Soc. Am., 9, 355, 1924.
[290] Mt. W. Contr., in press.
[291] J. Op. Soc. Am., 8, 609, 1924.
[292] Payne, Proc. N. Ac. Sci., 11, 192, 1925.
[293] Menzel, H. C. 258, 1924.
[295] Maury, H. A., 28, 79, 1900.
[296] Russell, Mt. W. Contr., in press.
[297] H. C. 258, 1924.
[299] loc. cit.
[300] A. Fowler, Proc. Roy. Soc., 73A, 219, 1904; M. N. R. A. S., 69, 508, 1909.
[301] Hale, Adams and Gale, Ap. J., 24, 185, 1906; Hale and Adams, ibid., 25, 75, 1907.
[302] Rep. of Spectral Class. Comm., I. A. U., 1925.
[303] W. F. Meggers, J. Wash. Ac. Sci., 13, 317, 1923; ibid., 14, 151, 1924.
[304] Menzel, H. C. 258, 1924.
[305] Ap. J., 25, 235, 1907.
[306] J. Op. Soc. Am., 9, 355, 1924.
[307] Catalan, An. Soc. Espan. Fis. y Quim., 21, 84, 1923.
[308] Russell, Mt. W. Contr., in press.
[310] Menzel, H. C. 258, 1924.
[311] J. Op. Soc. Am., 9, 335, 1924.
[312] Catalan, Phil. Trans., 223A, 127, 1922.
[314] H. C. 238, 1924.
[315] J. Op. Soc. Am., 9, 355, 1924.
[316] Phil. Trans., 223A, 127, 1922.
[317] Walters, J. Op. Soc. Am., 8, 245, 1924.
[319] Ibid.
[320] Pub. Dom. Ap. Obs., 3, 7, 1925.
[321] H. C. 258, 1924.
[323] Mt. W. Contr., in press.
[324] Walters, J. Wash. Ac. Sci., 14, 408, 1924.
[325] Russell, Ap. J., 55, 119, 1922.
[326] Menzel, H. C. 258, 1924.
[327] Ap. J., 9, 214, 1899.
[328] Russell, Ap. J., 55, 119, 1922.
[329] Menzel, H. C. 258, 1924.
[332] Pub. Dom. Ap. Obs., 2, 287, 1924.
[333] Meggers, J. Wash. Ac. Sci., 14, 419, 1924.
[334] Ibid.
[335] de Gramont, C. R., 171, 1106, 1920.
[336] Merrill, Pub. A. S. P., 33, 206, 1921.
[337] King, Pub. A. S. P., 36, 140, 1924.
[338] Kiess, Bur. Stan. Sci. Pap. 474, 1924.
[339] Catalan, An. Soc. Espan. Fis. y Quim., 21, 84 and 213, 1923.
[340] Russell, Science, 39, 791, 1914.
[341] M. N. R. A. S., 77, 487, 1907.
[342] Russell, Ap. J., 55, 119, 1922.
[343] Saha, Phil. Mag., 40, 472, 1920.
[344] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 325, 1922.
[345] M. C. Johnson, M. N. R. A. S., 84, 516, 1924.
[346] Menzel, H. C. 258, 1924.
[347] Kiess, Pub. Obs. Mich., 3, 106, 1923.
[348] Mitchell, Ap. J., 38, 407, 1913.
[349] Gousmid, Naturwiss., 41, 851, 1924.
[350] A. N., 191, 393, 1912.
[351] A. N., 192, 82, 1912.
[352] A. N., 192, 266, 1912.
[354] Abbot, The Sun, 92, 1911.
[Pg 89]
[Pg 90]
[Pg 91]
IT is certain that the conditions of which we see the integrated result in the stellar spectrum are exceedingly complicated. Unfortunately, the superficial portion of the star about which direct observational evidence can be obtained is far less tractable to theory than is the interior. Progress is only made possible by treating at the outset a simplified case, by aiming merely at approximate results, and in particular by limiting the preliminary discussion to the factors which are numerically the most effective. As an introduction to the theory of thermal ionization, the present chapter aims at the reconstruction and interpretation of a stellar spectrum by applying known physical laws under very simple conditions.
The stellar reversing layer may be represented by an optically thin layer of gas, at a pressure of the order of one ten thousandth of an atmosphere; it lies between the observer and a photosphere which radiates as a black body. The observer receives the radiation from both reversing layer and photosphere, which are regarded, in the present descriptive section, as independent. A more complete treatment would take account of the temperature and pressure gradients in the atmosphere of the star, the flux of energy, and the consequent intimate connection between reversing layer and photosphere. Actually they grade imperceptibly one into the other. The photosphere is that level in the atmosphere at which the general opacity cuts off the direct light from the interior;[355] in the case discussed the reversing layer is considered to be optically so thin that the general opacity is negligible. The selective opacity, depending on the natural absorption frequencies of the atoms present in the gas, gives rise [Pg 92] to the line absorption spectrum which we are about to consider; the region of sensible general opacity, represented by the photosphere, gives rise to a continuous spectrum corresponding to the continuous background in the star.
THE ABSORPTION OF RADIATION
The light passing through the layer of gas is absorbed, in terms of atomic theory, in the shifting of an electron from one energy level in an atom to some higher level, losing in the process energy of the definite frequency which is associated with that particular atom and energy transfer. The energy levels and possible electron transfers for the hydrogen atom are reproduced in Figures 2 and 3. In Figure 3 the horizontal lines represent the stationary states which can be assumed by the electron, and the arrows denote possible jumps from one stationary state to another. In Figure 2 the electron orbits corresponding to some of the simpler corresponding transitions for the hydrogen atom are represented. Arrows denote transfers from one orbit to another. The designation of the line corresponding to each transfer is appended to the appropriate arrow. It is evident that the occurrence of a given jump requires that there shall be an electron in the stationary state from which the jump originates.
The ultimate lines[356][357] are those which arise from the
lowest energy level, and are therefore those most readily absorbed by
the normal (undisturbed) atom. In the hydrogen spectrum these comprise
the Lyman series,[358] with the first member at 1215.68. The Balmer and
Paschen series are both subordinate series, requiring an initial
lifting of the electron from the lowest energy level into a two and
three (total) quantum orbit, respectively. The absorption of the Lyman
line Ly is necessary to a hydrogen atom before it is in a
fit condition to absorb any Balmer line, and for the absorption of a
Paschen line, an initial absorption of Ly
or H
is
required.
[Pg 93]
It appears plausible to assume, at least for low partial pressures, that the amount of energy of any frequency that is lost by black-body radiation in passing through the absorbing layer will vary jointly with the supply of energy and the number of atoms which are in a suitable state to absorb that particular frequency. One of the problems that arise is therefore that of determining what fraction of the whole number of atoms of a given kind will be able to absorb. It is to this problem that ionization theory is able to offer a solution.
By choosing the much simplified case of very low pressure and small
concentration, the effects of ionization by collision[359] and of
nuclear fields are probably eliminated. The remaining factor which may
influence the number of absorbing atoms is thermal ionization, and this
is actually the numerically important factor, as was first pointed out
by Saha.[360] It is of interest to note that Saha’s original treatment
contemplated pressures of the order of one atmosphere. Under such
conditions the effects of collisions and of nuclear fields are
not negligible, and might well have invalidated the theory. Later
work has shown conclusively, however, that the pressures in the
reversing layer are probably not greater than
,[361][362] and
that thermal ionization is the predominant factor under these conditions.
[Pg 94]
The absorbing layer is to be regarded as consisting of a mixture of all chemical elements, without any assumption as to quantity, so long as the partial pressure of each individual element is low. In other words, no account is taken, at the present stage, of the relative abundances of different kinds of atoms—the total effectiveness of the corresponding elements as absorbers. The changes in the absorption of the black body radiation by a given element with changing temperature will be the same whatever the partial pressure, provided it is low, and it is with these changes that the preliminary schematic discussion is concerned.
LOW TEMPERATURE CONDITIONS
At low temperatures all the elements will tend to be in their normal atomic state, unless they are aggregated into molecules or compounds. At temperatures of 2500°, which is about the lower limit encountered in dealing with stellar spectra, there is evidence of the existence of various oxides (CO, TiO₂, ZrO₂), of “cyanogen,” and of hydrocarbons, but most of the other possible compounds appear either to be dissociated or to be in very low concentration. Probably the normally polyatomic gases such as oxygen, nitrogen, and sulphur, are to some extent present in the molecular state. Even at atmospheric pressure all the metals are vaporized at 2500° excepting tantalum and the platinum metals, which boil at about 2800° under a pressure of 760 mm; at lower pressures the temperature of vaporization is, of course, lower. The metallic molecule appears normally to be monatomic, so that it will give its line spectrum unless it is in combination. The fact that silicon, the most refractory substance, excepting carbon, with which we have to deal, gives its line spectrum in the coolest stars known, indicates that all the elements may be considered to be gaseous in stellar atmospheres.
ULTIMATE LINES
The absorption spectrum given by the reversing layer when it is at a low temperature will consist of the lines given most readily by the atom in its normal state. The energy transfers which move an electron from its normal orbit to another correspond to the “ultimate lines,” and these lines will therefore be especially outstanding in the spectra of the coolest atmospheres. They are of such importance, from theoretical and from practical standpoints, that a list of them is reproduced here. Successive columns of the table give the atomic number and atom, the ionization potential, the wave-lengths of the ultimate lines, and an indication of their observed occurrence in stellar spectra. An asterisk denotes that the line has been observed, and a dash indicates that it has not been recorded.
[Pg 95]
It may be remarked that the ultimate lines of sodium, potassium, lithium, rubidium, and caesium are in the visible region—a fact which is utilized in the laboratory flame tests used in qualitative analysis.[363] The brilliancy of the flame colors obtained in the Bunsen burner, at the temperature of about 1500°C., is a striking elementary illustration of the readiness with which the atom in its normal state will take up and re-emit the frequency corresponding to the ultimate lines (second pair for K, Rb, Cs).
| Atom | Ionization Potential |
Wave-lenght | Stellar Ocurrence |
|
|---|---|---|---|---|
| 1 | H | 13.54 | 1215 | - |
| 2 | He | 24.47 | 584, 557 | - |
| 3 | Li | 5.37 | 6707 | * |
| 4 | Be | ? | 2349 | - |
| 5 | B | ? | 2498, 2497 | - |
| 6 | C | ? | 2479 | - |
| 7 | N | ? | - | - |
| 8 | O | 13.56 | 1306, 1304, 1302 | - |
| 9 | F | ? | - | - |
| 10 | Ne | 16.7 | - | - |
| 11 | Na | 5.12 | 5896, 5890 | * |
| 12 | Mg | 7.61 | 2852 | - |
| 13 | Al | 5.96 | 3962, 3944 | - |
| 14 | Si | ? | 2882 | - |
| 15 | P | ? | 2553, 2536 | - |
| 16 | S | 10.31 | 1915, 1900 | - |
| 17 | Cl | ? | - | - |
| 18 | A | ? | - | - |
| 19 | K | 4.32 | 7699, 7665 | * |
| 20 | Ca | 6.09 | 4227 | * |
| 21 | Sc | ? | 4247, 3652 | * |
| 22 | Ti | 6.5 | 5065, 5040, 5014 | * |
| 23 | V | ? | 4331, 4333 | * |
| 24 | Cr | 6.75 | 4290, 4275, 5254 | * |
| 25 | Mn | 7.41 | 4034, 4033, 4031 | * |
| 26 | Fe | ? | 2756, 2749 | - |
| 27 | Co | ? | 3454, 3405 | * |
| 28 | Ni | ? | 3415 | * |
| 29 | Cu | 7.69 | 3274, 3248 | * [Pg 96] |
| 30 | Zn | 9.35 | 2139 | - |
| 31 | Ga | 5.97 | 4172, 4033 | * |
| 37 | Rb | 4.16 | 7948, 7800 | * |
| 38 | Sr | 5.67 | 4607 | * |
| 40 | Zr | ? | 4496, 4392 | * |
| 42 | Mo | ? | 3903, 3864, 3798 | * |
| 47 | Ag | 7.54 | 3383, 3281 | * |
| 48 | Cd | 8.95 | 2288 | - |
| 49 | In | 5.76 | 4511, 4102 | * |
| 50 | Sn | ? | 3262 | ? |
| 55 | Cs | 3.88 | 8943, 8581 | - |
| 56 | Ba | 5.19 | 7911 | - |
| 57 | La | ? | 3949 | * |
| 79 | Au | 8.72 | 2676, 2428 | - |
| 80 | Hg | 10.39 | 2537, 1850 | - |
| 81 | Tl | 6.08 | 5350, 3775 | - |
| 82 | Pb | 7.38 | 4058, 3684 | * |
It is possible to predict from the table which lines are likely to appear in the spectra of the coolest stars. The ultimate lines of Al, K, Ca, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Ga, Rb, Sr, Zr, Mo, Ag, In, Ba, La, and Pb fall in the region ordinarily photographed, and Na can be reached in the yellow. All these elements in the neutral state would therefore be anticipated in the spectra of cooler stars, and they are indeed found without exception. The ultimate lines of several elements contained in the list lie in the far ultra-violet, and cannot be detected in stellar spectra. The corresponding neutral elements will therefore not be recorded unless they also give a strong subordinate series in the photographic region. The elements C, O, S, and probably N, all have ultimate lines in the ultra-violet, and possess no subordinate series in the appropriate range of wave-length. Their apparent absence in the neutral state from stellar spectra is therefore fully explained. All of these elements appear in the hotter stars in the once or twice ionized condition. The elements H, Mg, and Si have strong subordinate series in the photographic region—the Balmer [Pg 97] series, the “b” group, and the line[364] at 3905, respectively. They are accordingly represented in the cooler stars.
The elements contained in the table and not yet discussed are Be, B, Ne, A, F, and Cl. These elements have not been detected in stellar spectra. In seeking an explanation of their apparent absence, it has been suggested that a low relative abundance of the corresponding atoms may be responsible. Arguments from terrestrial analogy must be applied with caution, but there is reason to suspect that they may here have a legitimate application.[365] It may be suggested that boron, beryllium, neon, and argon are present in the stars in quantities too small to be detected. The halogens are unrepresented, but it is not possible to draw useful inferences until their laboratory spectra are more fully analyzed.
IONIZATION
At the lowest temperatures, then, the ultimate lines will predominate.
As the temperature of the absorbing layer is raised, ionization—the
complete ejection of the electron from the atom, instead of a
displacement from one stationary state to another—will set in, and
the tracing of the resulting spectral changes is the salient feature
of the Saha theory. “Ionization can be effected in many ways. To expel
an electron against the attractive force of the remainder of the
molecule, work is required, and the necessary energy may be furnished
by X rays or rays, or by collision with other electrons....
At high temperatures, when the conditions of maximum entropy demands an
appreciable amount of ionic dissociation, the requisite energy is drawn
from the environment.... The work required to ionize a single molecule,
when expressed as the number of volts through which an electron must
fall to acquire this energy, is the ionization potential; it may
be regarded as the latent heat of evaporation of the electron from the
molecule” (Milne).[366]
[Pg 98]
The analogy between ionization and evaporation illustrates very well the scope of the Saha theory, in which the process is treated as a type of chemical dissociation. Corresponding to each temperature there is a definite state of equilibrium, where the forward and backward velocities of the ionization process are equal—in other words where ionization and recombination are proceeding at the same rate. The method of statistical mechanics has been applied to this problem by Fowler and Milne.[367] Here the analysis will not be reproduced, but the formulae are required in order to illustrate the process of ionization.
The number of atoms which are unionized at any given temperature is
given by the expression
where
= number of atoms ionized.
= the “partition function.”
, where
is the partial pressure of electrons.
= absolute temperature.
= Boltzmann’s constant, =
.
= the ionization potential.
This is the number of atoms which is effective in absorbing the
ultimate lines at that temperature. For low values of , the
number of unionized atoms falls off at first very slowly with rising
temperature, up to a point depending only on the ionization potential.
Beyond this temperature the number of neutral atoms falls off with
great rapidity. The diagram (Figure 5) illustrates the fall in the
number of neutral atoms, and the consequent decay in strength of the
ultimate lines. So steep is the gradient of
at the higher
temperatures that the quantity is best plotted logarithmically. The
ultimate lines will persist, with almost undiminished intensity, up to
the temperature at which the gradient of
begins to increase.
[Pg 99]
This critical temperature increases with ionization potential, and
neutral atoms of high ionization potential should display very
persistent ultimate lines as the temperature rises.
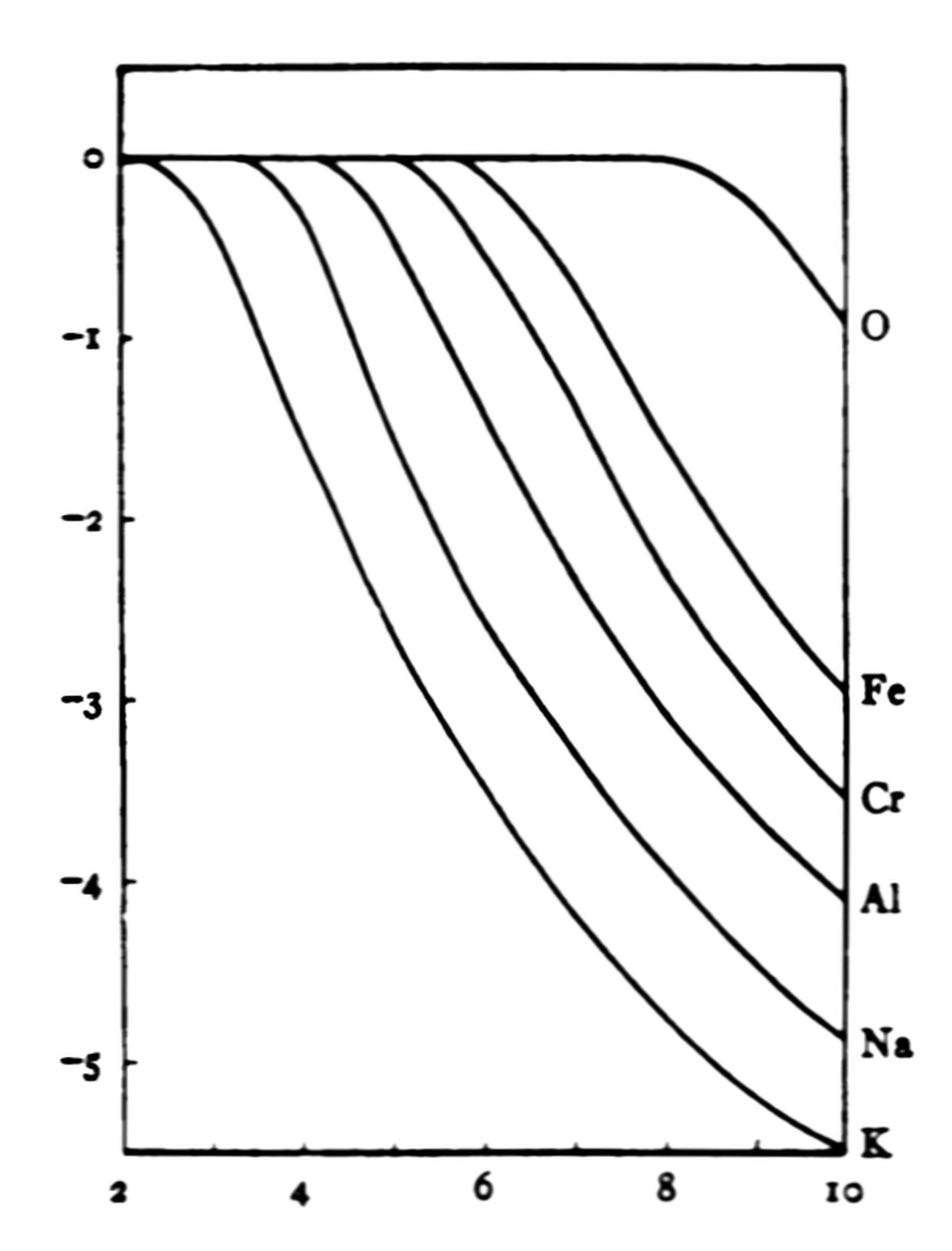
Figure 5
Ultimate lines of neutral atoms. Ordinates are logarithms of computed fractional concentrations; abscissae are temperatures in thousands of degrees. The curves show the decrease in the number of neutral atoms, with rising temperature, and the consequent decay in strength of the ultimate lines, for the atoms indicated on the right margin.
As ionization becomes more and more complete, the intensity of the ultimate lines falls off until so small a number of neutral atoms remains that their lines cease to appear in the absorption spectrum.
SUBORDINATE LINES
The neutral atom gives rise to other lines besides the ultimate lines, but these require the transfer of an electron from some stationary state, not the normal one, to another stationary state. The atom must receive a definite quantity of energy, equal to the excitation potential of the initial stationary state, in order to be in a condition to absorb a line of a subordinate [Pg 100] series which originates from that state. If there is an appreciable energy supply, a certain fraction of the neutral atoms present will have received this excitation energy, which is of course smaller than the ionization potential, and these atoms will be in a position to absorb the subordinate series.
Figure 6
Production of the maximum of an absorption line. Ordinates are logarithms of computed fractional concentrations; abscissae are temperatures in thousands of degrees. The curves reproduced are those for the Mg + line at 4481. The upper broken curve represents the fraction of magnesium atoms that is singly ionized at the corresponding temperature; the lower broken curve represents the fraction of the Mg + atoms present that is in a suitable state for the absorption of 4481. The full line represents the sum of the ordinates of the dotted curves, and gives the fraction of the total number of magnesium atoms that is able to absorb 4481 at the various temperatures indicated by the abscissae.
The fraction, , of the total number of neutral atoms which have
[Pg 101]
become able to absorb the lines associated with a definite excitation
potential is given by Fowler and Milne as
where (
) = excitation potential. The quantity
increases with the temperature, approaching the value unity
asymptotically.
The total number of atoms active in absorbing a subordinate series
at any temperature is evidently the product of the number of
neutral atoms and the quantity . The curves for these
two quantities are plotted logarithmically in Figure 6, the magnesium
line 4481 being used as an illustration. The total number of absorbing
atoms may be obtained by adding the ordinates. It will be seen that the
number of such atoms increases, passes through a maximum and decreases
again, as the temperature is raised. The maximum for a subordinate
line of the neutral atom may occur, as in the case of helium, when
ionization is far advanced.
In the special case where , the second
curve, which represents the growth of the fraction
, becomes
a straight line parallel to the temperature axis, and the first, or
ionization, curve, approaches the zero ordinate asymptotically at low
temperatures. The ordinate of the curve representing
is zero,
and the resultant sum gives a curve identical with the curve for the
ultimate lines. Ultimate lines thus appear as the special case of
subordinate lines for which the excitation potential is zero. This fits
exactly with the definition of ultimate lines as the lines naturally
absorbed by the cold vapor—no initial excitation is required to bring
the atoms into a state in which they can absorb.
LINES OF IONIZED ATOMS
[Pg 102]
As soon as ionization sets in, the absorbing layer begins to contain a new kind of atom, derived from the neutral atoms by the complete ejection of one electron. These ionized atoms will absorb their own spectrum, which differs completely from that of the corresponding neutral atom; and the degree of absorption will again depend on the number of such ionized atoms present in the reversing layer.
The ionized atom has in general a spectrum corresponding
exactly to that of the neutral atom preceding it in the periodic
table, but with a different Rydberg constant.[368][369] Two types of
lines arise, as before—ultimate and subordinate lines. For
the number of atoms which can absorb the ultimate lines of the
enhanced spectrum, the formula reduces to
Account is here taken of the residual neutral atoms by the
middle term of the denominator, which is very small, and is
only of sensible magnitude for the ultimate lines, when the
numerator is equal to unity.
Figure 7
Maximum of the ultimate line of an ionized atom. Ordinates are
logarithms of computed fractional concentrations; abscissae are
temperatures in thousands of degrees. The curve is drawn for
the line 4554 of Ba+, on the assumption that is
.
The following curve shows the number of absorbing atoms. The flatness
of the maximum is especially to be noted, suggesting that the ultimate
lines of the ionized atom, like the ultimate lines of the neutral
[Pg 103]
atom, will be very persistent. The and
lines of Ca+, and
the corresponding lines 4077 and 4215 of Sr+, and 4555 of Ba+, would
thus be expected to show over a considerable range in temperature and
spectrum, and this is actually found to be the case.
The subordinate lines behave substantially as do the subordinate lines of a neutral atom, rising to a maximum at a temperature which depends chiefly on the ionization potential. It is assumed in deriving the corresponding equations that in practice the number of surviving neutral atoms will be too small to affect the concentration of ionized atoms giving the subordinate lines. This assumption may be shown to be justified at maximum intensity of the absorption line, though possibly the neutral atoms are not always negligible at the first appearance of the ionized lines of a very abundant atom.
SUMMARY
The general results of raising the temperature of the absorbing layer have now been traced. Although a greatly simplified case has been considered, the observed changes in the stellar spectral sequence have been very satisfactorily predicted.
At low temperatures the lines of neutral atoms are strong, in particular the ultimate lines, such as 3930 of Fe, 3999 of Ti, 4254 of Cr, and 4033 of Mn, which are at maximum strength, and decrease at first slowly, then rapidly in the hotter stars. The subordinate lines of neutral atoms, 4455 of Ca and 4352 of Fe, for example, attain a maximum, and then fall off with rising temperature. For many of the metallic lines for which no maximum is recorded, like those of the subordinate series of Na, the theoretical maximum is at a temperature equal to that of the coolest stars examined. Atoms with ionization potential less than 5 volts will in general give maxima below 3000°.
As the temperature increases, the lines of ionized atoms begin to appear, the ultimate lines rising very quickly in intensity, and persisting almost at maximum over several spectral classes. Later in the sequence the subordinate series for ionized atoms [Pg 104] appear, rise to a sharper maximum, and fade more rapidly. The 4481 line of Mg+, the 4267 line of C+, and the 4128 line of Si+, show this effect well.
As the fall of intensity of the lines of neutral atoms after maximum
is the result of the progress of ionization, it would be expected that
the lines of the ionized atom would appear while those of the neutral
atom were still quite strong, and that the one series would rise in
strength as the other decreased. The lines of the neutral atom may
persist over a large part of the range of the ionized lines. This is
the case with the 4227 line of Ca, which persists until Class ,
while the
and
lines of Ca+ have been visible throughout
the whole spectral sequence, and have been decreasing in intensity
from
onwards, owing chiefly to the rise of second ionization
and the consequent formation of Ca++, which gives a spectrum in the
ultra-violet and is therefore not detected in the stars.
As the temperature is further raised, the second and third ionizations set in, and presumably follow the same procedure as has been outlined for less ionized atoms. The lines of N++, C++, Si++, and Si+++ will serve as examples. The lines of the doubly ionized atoms of the metals are in general in the ultra-violet portion of the spectrum, and the corresponding elements do not therefore appear in the hotter stars, where they would otherwise be anticipated.
Qualitatively the prediction of the theory of ionization is fully satisfied. The quantitative discussion involves more rigorous treatment, and is reserved for a later chapter.
[355] Stewart, Phys. Rev., 22, 324, 1923.
[356] De Gramont, C. R., 171, 1106, 1920.
[357] Russell, Pop. Ast., 32, 620, 1924.
[358] A. Fowler, Report on Series in Line Spectra, 1922.
[359] R. H. Fowler, Phil. Mag., 47, 257, 1924.
[360] Proc. Roy. Soc., 99A, 135, 1921.
[361] M. N. R. A. S., 83, 403, 1923; ibid., 84, 499, 1924.
[362] Russell and Stewart, Ap. J., 59, 197, 1924.
[363] Eder and Valenta, Atlas Typischer Spektren, 10, 1911.
[366] Milne, Observatory, 44, 264, 1921.
[367] M. N. R. A. S., 83, 403, 1923; 84, 499, 1924.
[368] Sommerfeld, Atombau und Spektrallinien, 457, 1922.
[369] Meggers, Kiess, and Walters, Journ. Op. Soc. Am., 9, 355, 1924.
[Pg 105]
THE theory of thermal ionization, of which the preceding chapter contains an illustrative discussion, may be treated from two points of view—the sufficiency of the analytical treatment, and the nature of the underlying physical assumptions. Actually the two questions are merely two different ways of regarding the validity of the theory, but they divide the discussion conveniently into a section dealing with the analytical treatment and a section dealing with the physical assumptions.
The original treatment by Saha[370] was based on the Law of Mass Action, and the application to stellar atmospheres raised questions of a physical rather than of an analytical nature. These questions are fundamental not only to the Saha treatment, but also to the more recent development of the theory, and they will be discussed in the second half of the present chapter. The first half will be devoted to the analytical formulae.
MARGINAL APPEARANCE AND MAXIMUM
Saha’s discussion was based on the observation of “marginal appearance”—the spectral class at which a particular absorption line is at the limit of visibility. The use of this quantity as a criterion for the temperature scale has certain practical drawbacks. Marginal appearance depends directly on relative abundance, since a more abundant element will give visible lines at a lower “fractional concentration,” that is to say, when a smaller fraction of the element is contributing to the lines in question. Further, in estimating the intensities of lines in stellar spectra, difficulty is experienced when the lines are faint, and the spectral class at which they are first or last seen depends on their width and definition, the intensity [Pg 106] of the continuous background, the presence of other lines, and the dispersion used. All of these factors are subject to variation, and in particular the intensity distribution in the continuous background changes with the temperature. The statistical theory of Fowler and Milne has, therefore, a great advantage in that it leads to an estimate of the temperature at which a given line attains maximum. A maximum, unlike a marginal appearance, can be determined without ambiguity from homogeneous material, whatever the dispersion. In the cooler stars the estimates may be made difficult by blending, but the uncertainty can generally be removed by examining the maxima of several related lines. Of the observational factors enumerated above as affecting the estimation of marginal appearance, the changing intensity distribution of the continuous background with the temperature is the only one that may prove serious for the method of maxima.
THEORETICAL FORMULAE
The theory developed by Fowler and Milne has been exhaustively discussed by these authors in several papers, and it appears unnecessary to reproduce the analysis in detail. The ionization and excitation curves have been treated diagrammatically in the previous chapter. The detailed formulae follow.
“If is the ionization potential of the atom,
the (negative) energy of a given excited state, then
for a given partial electron pressure
of free electrons, the
temperature
of maximum concentration of atoms in the given
excited state
is given by[371]
[Pg 107]
“The temperature at which the concentration of singly ionized atoms
reaches a maximum is given by[372]
The two formulae that have been quoted assume, in effect, that at any stage of ionization the number of atoms, in stages other than those whose constants appear in the formulae, is negligible. When two ionizations occur in very close succession, this assumption no longer holds, and the equations, as modified to embody the necessary correction, are as follows.[373]
For the subordinate series of a neutral atom,
“This equation must be used to calculate whenever
the ionization potential of the stage in question is closely
followed by the ionization potential of the succeeding stage.”
For the subordinate series of the ionized atom,
[Pg 108]
This equation “must be used wherever the ionization potential of
the stage in question is closely preceded by the ionization
potential of the preceding stage. The corrections ... result in making
the maxima for the lines of the two stages occur farther apart in
the temperature scale. If we express the correction in the
form of a factor (
) ... then
is of the order
. Since
varies
roughly as
or
, we see that the importance of the
correction is determined by the closeness of
to 1.”
The values of , the fractional concentration of the atom in
question, are obtained through the application of the ordinary methods
of statistical mechanics to the equilibrium between atoms and electrons
in the reversing layer. The values of
at the maximum are
obtained by differentiating the expression for
with respect to
, and equating to zero, since the maximum of absorption will occur
when
is at a maximum.
The analytical treatment calls for no comment. Its basis has been fully
discussed by R. H. Fowler[374] in a series of papers. The weights
() of the atomic states employed were based on the work of
Bohr[375] on the relative values of the a priori probabilities of the
different stationary states for hydrogen. On this view,
for all atoms excepting those of H and He+, for which it is equal to
2. The convergence of the series for
was not established by
Fowler and Milne, but the authors regard the subsequent investigation
by Urey[376] as justifying their assumption that “for physical reasons
one must suppose the series effectively cut off after a certain number
of terms. Usually the series then reduces (as regards its numerical
value) practically to its first term.”
PHYSICAL CONSTANTS REQUIRED IN THE FORMULAE
The application of the equations will of course depend upon an accurate
knowledge of the constants involved. The quantities ,
,
, and
require no comment. The symmetry number
[Pg 109]
of the neutral atom is in effect the number of spectroscopic
valency electrons given in Bohr’s table,[377] for the atoms for which
it is known. In all the applications made by Fowler and Milne the
quantity was equated to 1 or 2, and it is very probable that this
number is not in any case exceeded. For carbon, where the chemical
valency is equal to 4, the value of
is still 2, as has
been shown by Fowler’s analysis of the spectrum of ionized carbon.[378]
The value of
is not known for atoms in the long periods,
but in the present work it is assumed to be 1 and 2 for atoms with
arc spectra which show even and odd multiplicities, respectively. The
uncertainty in the value of
introduces only a relatively
small error into the result, since
depends on the first power
of
, and in no case considered can
exceed five.
The most important factor involved in the theory is ,
the partial pressure of electrons in the reversing layer.
By assuming
constant at about
, and treating
as the unknown, a temperature scale which agrees substantially
with those derived from measurements of radiation may be deduced from
the observed positions of the maxima. The first discussion of the
data then available was made by Fowler and Milne in their original
paper.[379] Subsequent investigations of the positions of maxima
have been published by Menzel[380] and by the writer.[381] These
observations, and the scale derived from them, will be discussed in the
two following chapters.
The value of has been recently shown by several kinds of
investigation to be at least as low as was assumed by Fowler and
Milne, so that their assumption that a uniform mean pressure can be
used, as a first approximation, in deriving a temperature scale from
their formula appears to be justified. Milne[382] points out that “on
whatever specific assumptions” the theory rests, “the mean pressure for
a maximum of intensity in an absorption line is found to depend on the
absolute value of the absorption coefficient. In fact ... it is clear
[Pg 110]
that the greater the absorbing power of the atoms in question, the more
opaque is the stellar atmosphere in the frequency concerned, and so
the greater the height and the smaller the pressure at which the line
originates.” That the absorption coefficient in the stellar atmosphere
is very high is suggested by the reorganization times (“lives”) of such
atoms as have been investigated,[383] and Milne’s discussion of the
life of the excited calcium atom from astrophysical data lends weight
to the suggestion. A high absorption coefficient leads at once
to low pressures in the reversing layer, and theory has gone
far towards indicating that pressures of the order of
are to be expected
on a priori grounds.[384]
The observational evidence bearing on pressures in the reversing layer will be found[385] in Chapter III. The case appears to be a strong one, resting on evidence of many different kinds—notably pressure shifts, line sharpness, and series limits. Russell and Stewart,[386] in their exhaustive discussion of the question, conclude that “all lines of evidence agree with the conclusion that the total pressure of the photospheric gases is less than 0.01 atmosphere, and that the average pressure in the reversing layer is not greater than 0.0001 atmosphere.”
The observational evidence gives the total pressure, but the partial electron pressure will not differ greatly from this. Although even in the hottest stars three ionizations is the greatest number observed, most of the elements that constitute the stellar atmosphere are appreciably ionized at temperatures greater than 4000°, so that the partial electron pressure is at least half the total pressure.
PHYSICAL ASSUMPTIONS
The method applied by Saha to stellar atmospheres was borrowed from physical chemistry. The Law of Mass Action, and the theory of ionization in solutions which is based upon it, have in general been very well satisfied in dilute solution.[387] The ionization considered [Pg 111] by chemical theory is the separation of a molecule in solution into charged radicals. The essential point is the acquisition of a charge at dissociation, and this is the only feature that the chemical ionization has in common with the thermal ionization, where the atom is separated into a positively charged ion and an electron which constitutes the negative charge.
The step from the theory first formulated for solutions to the theory
of gaseous ionization is a long one, and its legitimacy has been
questioned.[388] It appears, however, that the step is justified.[389]
The stellar conditions are certainly simpler than those in a
solution, and if the requisite dilution obtains, the law may be
expected to hold with considerable closeness. Saha contemplated
pressures of the order of an atmosphere, and it may be shown that under
such conditions the volume concentration would be too great and the
theory would be invalid. At pressures of
, however, the
effect of concentration is just becoming inappreciable, and the theory
probably holds with fair exactness.
LABORATORY EVIDENCE BEARING ON THE THEORY
(a) Ultimate Lines[390]—The physical tests of the Saha theory that have been made in the laboratory have all supported it strongly. The fact that the ultimate lines of an atom are the lines normally absorbed by the cold vapor has long been familiar. Indeed it is this fact that is tacitly assumed in the identification of lines of zero excitation potential in the laboratory with lines which are strongest in the low-temperature furnace spectrum. De Gramont[391] designated the ultimate lines “raies de grande sensibilité” for the detection of small quantities of a substance, because they are the last to disappear from the flame spectrum when the quantity of the substance is decreased.
[Pg 112]
(b) Temperature Class.—The effect, upon the absorption spectrum of a substance, of raising the temperature has also long been recognized as an increase in the strength of lines associated with the higher excitation potentials. The use of A. S. King’s “temperature class” in assigning series relations[392] involves a tacit admission of the validity of the theory of thermal ionization in predicting the relative numbers of atoms able to absorb light corresponding to different levels of energy.[393]
(c) Furnace Experiments.—King’s explicit investigation[394] of the effects of thermal ionization in the furnace has contributed valuable positive evidence for the theory. For example, the production of the subordinate series of the neutral atoms of the alkali metals by raising the temperature was an experimental proof of the principle mentioned in the last paragraph; and the suppression of the enhanced lines of calcium by the presence of an excess of free electrons, derived from the concurrent ionization of potassium, with an ionization potential 1.77 volts lower than that of calcium, and the similar results obtained for strontium and barium, fulfill the predictions of ionization theory in a striking fashion.
[Pg 113]
(d) Conductivities of Flames.—The conductivity of a flame may be used as a measure of the ionization that is taking place at the temperature in question, and the available data on flame conductivities have been discussed by Noyes and Wilson[395] from the standpoint of the theory of thermal ionization. The calculations based upon the conductivities imparted to a flame by the different alkali metals, and leading to an estimate of the ionization constant, were in satisfactory agreement with the theoretical predictions of the ionization constant from the known critical potentials. The theory of thermal ionization is, therefore, strongly supported by all the laboratory investigations which have so far been undertaken in testing it.
SOLAR INTENSITIES AS A TEST OF IONIZATION THEORY
Before proceeding to discuss the stellar intensity curves, it is proposed to review some of the solar evidence, which can be treated as an observational test of the predictions of the theory relating to the distribution of atoms among the possible atomic states at a given temperature.
In two papers, Russell[396] has given a discussion of the solar and sunspot spectra, showing that ionization theory offers a very satisfactory interpretation of most of the observed phenomena. Attention was called to the anomalous behavior of barium and lithium,[397] and it was suggested that the theory of thermal ionization, while taking account of the temperature of the reversing layer, omitted to consider the effect of the absorption of photospheric radiation. This omission might cause a deviation such as is observed for barium, but appears inadequate to account for the behavior of lithium. In the case of lithium, low atomic weight, and a consequent high velocity of thermal agitation, has been suggested as the cause of the anomaly. The question of the absorption of photospheric radiation has more recently been discussed by Saha,[398] in the form of a correction to his own ionization equations. It has been pointed out by Woltjer[399] that the correction introduced by Saha and Swe may also be derived from considerations advanced by Einstein[400] and Milne.[401] The correction can be evaluated, but appears in every case to be rather small. The effect of the photospheric radiation is certainly one that must be included in a satisfactory theory, but at present, observation is probably not of sufficient accuracy to demand such a refinement.
The work just quoted was qualitative. A more quantitative test of ionization theory in the solar spectrum can also be made[402] by comparing the intensities of solar lines corresponding to different excitation potentials, but belonging to the same atom. The [Pg 114] atoms which give a large number of lines in the solar spectrum are those of the first long period of the periodic table, and these, as is well known, consist of multiplets, with components of very different intensities. It appears to be legitimate to select the strongest line associated with any energy level for the comparison; the strength of this line probably represents fairly well the tendency of the atom to be in the corresponding state.
| Atom | Excitation Potential |
|
Intensity | Atom | Excitation Potential |
|
Intensity |
|---|---|---|---|---|---|---|---|
| Calcium | 0.00 | 20 | Chromium | 0.00 | 10 | ||
| 1.88 | 15 | 0.94 | 5 | ||||
| 2.53 | 8 | 1.02 | 5 | ||||
| 2.70 | 5 | 2.89 | 2 | ||||
| 2.92 | 4 | Titanium | 0.00 | 5 | |||
| Iron | 0.00 | 40 | 0.82 | 4 | |||
| 0.94 | 30 | 0.90 | 3 | ||||
| 1.54 | 30 | 1.05 | 3 | ||||
| 2.19 | 8 | 1.44 | 3 | ||||
| 2.46 | 10 | 1.50 | 2 | ||||
| 2.84 | 8 | 1.87 | 1 | ||||
| 2.96 | 7 | 1.98 | 1 | ||||
| 3.25 | 7 | 2.08 | 0 | ||||
| 3.38 | 6 | 2.16 | 1 | ||||
| 3.64 | 8 | 2.24 | 2 | ||||
| 4.13 | - | 2.26 | 0 | ||||
| 4.23 | - | 2.28 | 0 | ||||
| 4.35 | - | 2.33 | 0 | ||||
| 4.40 | - | 2.39 | 00 | ||||
| 2.47 | - | ||||||
| 2.56 | 000 | ||||||
| 2.67 | 000 |
The atoms for which there are enough known lines of different excitation energies in the solar spectrum are those of calcium, chromium, titanium, and iron. The correlation between the excitation potential associated with a given line and the intensity of the line in the solar spectrum is illustrated by the preceding tabulation. Successive columns give the atom, the excitation potential, the [Pg 115] computed fractional concentration, expressed logarithmically, and the observed intensity, taken from Rowland’s table.
It will be seen that the correlation is very marked, and that it appears to furnish good evidence that the theory of thermal ionization predicts correctly the relative tendencies of the atoms to absorb the different frequencies. The fractional concentrations are of course not absolute values, as the number of atoms in a state of high excitation is a definite fraction, not of the whole number of atoms, but of the number left over from the lower excitations. Neither are the intensities given by Rowland absolute, and therefore the comparison appears sufficient to show the strong correlation between excitation potential and solar intensity.
[370] Proc. Roy. Soc., 99A, 136, 1921.
[371] M. N. R. A. S., 83, 403, 1923; ibid., 84, 499, 1924.
[372] M. N. R. A. S., 83, 403, 1923.
[373] M. N. R. A. S., 84, 499, 1924.
[374] R. H. Fowler, Phil. Mag., 45, 1, 1923.
[375] Bohr, Mem. Ac. Roy. Den., 4, 2, 76, 1922.
[376] Ap. J., 59, 1, 1924.
[378] Proc. Roy. Soc., 103A, 413, 1923.
[379] M. N. R. A. S., 83, 404, 1923.
[380] H. C. 258, 1924.
[381] H. C. 252, 256, 1924.
[382] Phil. Mag., 47, 209, 1924.
[384] Proc. Phys. Soc. Lond., 36, 94, 924.
[386] Ap. J., 59, 197, 1924.
[387] See, for instance, H. J. H. Fenton, Outlines of Chemistry, 128, 1918.
[388] Lindemann, quoted by Milne, Observatory, 44, 264, 1921.
[389] Milne, Observatory, 44, 264, 1921.
[391] C. R., 171, 1106, 1920.
[392] Russell, Ap. J., in press.
[393] A. S. King, Mt. W. Contr. 247, 1922.
[394] A. S. King, Mt. W. Contr. 233, 1922.
[395] Ap. J., 57, 20, 1923.
[396] Mt. W. Contr. 225, 1922.
[397] Mt. W. Contr. 236, 1922.
[398] Saha and Swe, Nature, 115, 377, 1925.
[399] Nature, 115, 534, 1925.
[400] Phys. Zeit., 18, 121, 1917.
[401] Phil. Mag., 47, 209, 1924.
[402] Payne, Proc. N. Ac. Sci., 11, 197, 1925.
[Pg 116]
THE observational test of ionization theory involves a considerable program of measurement, if the accuracy necessary for a quantitative test is to be attained. The present chapter contains a synopsis of new data obtained by the writer to supplement the material already published in Harvard Circulars.[403][404] The data here presented practically complete the available material for the strong lines of known series relations in the region of the spectrum usually examined.
LINE INTENSITY
The theory predicts the degree of absorption that will be produced by each atom at a given temperature, and the related quantity that is measured is the intensity of the corresponding Fraunhofer line in the spectrum of the star. Spectrum lines are differentiated by various qualities, such as width, darkness, and wings, and their conspicuousness is governed by the intensity of the neighboring continuous background. It is not easy to specify all these quantities on an intensity scale that is one-dimensional, and the various ways in which line intensities have been estimated represent different attempts to choose and express a suitable scale.
Many of the applications of so-called line-intensity, such as the estimation of spectroscopic parallaxes, have involved ratios between the strengths of various lines in the same spectrum. This method of comparison avoids most of the difficulties caused by differences of line character and continuous background, for the lines that are to be compared are chosen because of their proximity and comparability. [Pg 117] Harper and Young[405] have standardized the method by comparing spectrum line ratios with line ratios on an artificial scale.
METHOD OF ESTIMATING INTENSITY
In a comparison of ionization theory with observation, some measure of line-intensity is required which can be compared from class to class. It seems probable that direct estimates of intensity, for spectra of the same dispersion, density, and definition, will be comparable within the limits of accuracy of the material.
Two series of spectra were measured by the writer in order to obtain
material for the test of the theory of ionization. For the first
group standard lines in the spectrum of Cygni were used
for the formation of a direct intensity scale, and for the second
group, comprising the cooler stars, a strip of the solar spectrum was
similarly employed. An arbitrary scale was constructed by assigning a
series of intensities to well placed lines in the spectrum, and using
these as standards. A list of the lines used for the second group, the
assigned intensity, and the intensity as given in Rowland’s table, are
contained in the following table.
| Line | Intensity | Line | Intensity | |||
|---|---|---|---|---|---|---|
| Assigned | Rowland | Assigned | Rowland | |||
| 4034 | 6 | 7 | 4046 | 10 | 30 | |
| 4035 | 5 | 6 | 3968 | 13 | 700 | |
| 4038 | 4 | 4 | 3934 | 15 | 1000 | |
| 4064 | 8 | 20 | ||||
[Pg 118]
The estimates thus made might be defined as estimates of width-intensity-contrast between the line and the continuous background. On an ideal plate which was not burned out, such estimates would give a measure of the total energy of the line relative to the neighboring continuous spectrum. The accuracy attained by direct estimates of this kind appears to be as great as the material warrants.
ACCURACY OF THE ESTIMATES
It is not possible at present to evaluate the accuracy of these
estimates with the same precision as for other physical quantities,
but the consistency of the readings from comparable plates of the
same star will at least give a measure of the value of the estimates.
Table XVIII contains the measures on forty-three lines in the spectrum
of Gruis, taken from six plates of the same dispersion,
and comparable quality, density, and definition. Successive columns
give the wave-length, the arithmetic mean intensity, and the standard
deviation
.
| Line | Int. | Line | Int. | Line | Int. | Line | Int. | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4215 | 8.4 | 1.0 | 4319 | 4.8 | 0.8 | 4376 | 7.8 | 0.6 | 4451 | 4.5 | 1.5 |
| 4227 | 16.0 | 1.4 | 4321 | 4.0 | 0.0 | 4379 | 4.2 | 0.3 | 4455 | 5.0 | 1.0 |
| 4247 | 6.0 | 0.0 | 4326 | 10.4 | 0.5 | 4383 | 10.3 | 0.8 | 4462 | 6.0 | 0.8 |
| 4250 | 7.0 | 0.0 | 4330 | 4.6 | 0.8 | 4395 | 6.3 | 0.4 | 4482 | 7.7 | 0.7 |
| 4254 | 9.0 | 1.0 | 4332 | 3.6 | 0.5 | 4398 | 2.7 | 0.8 | 4490 | 7.3 | 0.4 |
| 4260 | 9.0 | 2.1 | 4333 | 4.0 | 0.0 | 4402 | 6.3 | 0.4 | 4495 | 7.5 | 0.4 |
| 4272 | 8.7 | 0.8 | 4337 | 8.7 | 0.8 | 4405 | 9.0 | 0.5 | 4502 | 6.0 | 0.0 |
| 4275 | 9.5 | 1.3 | 4340 | 9.5 | 1.1 | 4409 | 9.0 | 0.5 | 4554 | 5.3 | 0.4 |
| 4283 | 4.3 | 0.4 | 4352 | 9.2 | 1.1 | 4415 | 7.7 | 0.8 | 4564 | 5.8 | 0.7 |
| 4290 | 10.6 | 1.0 | 4360 | 6.8 | 1.0 | 4435 | 9.2 | 0.9 | 4572 | 6.0 | 1.0 |
| 4315 | 8.3 | 0.7 | 4370 | 6.8 | 0.6 | 4444 | 8.9 | 1.2 |
These measures are strictly representative of the material as a whole,
for the plates of Gruis were measured at wide intervals in
the ordinary course of the work, and were selected for illustration
because there was a greater number of suitable plates of this star than
for any other.
HOMOGENEITY OF MATERIAL
The observational material on line-intensities follows in tabular form.
The measures were made in two groups, comprising respectively the
hotter stars and the stars cooler than Class , and different
intensity scales were used for the two. The solar scale mentioned above
was used for the second group of stars; the first group was referred
[Pg 119]
to standard lines in the spectrum of
Cygni. The distribution
of the stars in the two groups among the spectral classes was as
follows:
| Group I | ||||||||
|---|---|---|---|---|---|---|---|---|
| giants | 4 | 7 | 7 | 6 | 8 | 6 | 3 | 17 |
| super-giants | - | - | - | - | 2 | 1 | - | - |
| Group II | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dwarfs | - | - | - | - | - | 4 | 1 | 2 | 3 | 2 | 2 | - | - | - | - | - | - |
| giants | 1 | 9 | 3 | 5 | 2 | - | - | - | - | 3 | 5 | 20 | 4 | 8 | 1 | 5 | 1 |
| super-giants | - | - | - | - | - | 3 | 1 | 5 | 1 | 2 | - | 2? | 1? | 1? | 3 | 1 | - |
If it were possible to use a series of giants throughout, the task of determining the intensity maxima would be greatly simplified. Among the hotter stars the differences introduced by absolute magnitude are not great enough to make the maxima difficult to determine. With later classes, however, the changes with absolute magnitude are very marked. As will be pointed out in an ensuing chapter,[406] the actual strength of the lines differs considerably from giant to dwarf, owing to the difference in the effective optical depth of the photosphere. This difference in strength is in addition to the well-known “absolute magnitude effect” which is shown, for example, by the enhanced lines; it increases the difficulty of making estimates of line change from one class to the next, since, owing to selection, the available stars are far from homogeneous in absolute magnitude. In addition to this factor, there is the practical difficulty of making comparable estimates on the sharp narrow lines of a super-giant and those of a dwarf, since the lines of a dwarf tend to be hazy and lack contrast with the background.
It might be expected, from the distribution in luminosity of the
stars used, that irregularities in the intensity sequence would
probably occur in the classes and at
. For the purpose
of estimation of maxima, the
classes are not of very great
importance, as few of the maxima under present investigation occur
there, but the irregularity at
may well prove to be serious.
[Pg 120]
There is indeed a general tendency for the intensity of, metallic lines
to increase at
. All the
stars measured were of very
high luminosity, and probably the rise of intensity is due to this
feature, or rather to the increase of material above the photosphere
that accompanies it. A maximum is only assumed to occur at
when
a line increases regularly through the
types, as do the lines of
neutral calcium. The iron and titanium maxima obviously occur earlier
in the sequence, although the lines of both these elements are often
noticeably strengthened at
.
The following tabulation contains the data on line-intensity for all the lines of known series relations that have been measured up to the present. All the measures were made by the writer, excepting those for zinc, which are taken from Menzel’s paper.[407] Successive columns of the table contain the atom, the series relations, the wave-length, and the observed intensities in the various spectral classes. The column headed “Blends” is a direct transcription from Rowland’s tables, and contains details both of the line under consideration and of closely adjacent lines. The column headed “Remarks” contains the writer’s own conclusions, based on solar evidence, astrophysical behavior, and laboratory affinities, as to the source and maximum of the line that has been measured.
[Pg 121]
The recorded intensities, for classes cooler than , are derived
from the selection of stars mentioned earlier in the present chapter. A
list of the individual stars is contained in Appendix III. Four typical
stars have been selected to represent that class. The figures in the
final column refer to the notes to the table, which are listed under
the respective atoms, and give the observed maximum, the intensities
and origins of blended lines (in Rowland’s notation), and short
remarks, which indicate whether or no the observed behavior is to be
attributed to the line considered. Maxima that are obviously due to
another line are placed in parentheses.
| Atom | Series | Notes | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | 3970.1 | 20.0 | 17.6 | 20.0 | 15.6 | 15.0 | 17.2 | 17.8 | .. | 18.0 | 20.0 | 24.5 | .. | .. | 30.0 | .. | 1 | |
| 4101.7 | 18.0 | 16.0 | 16.3 | 13.6 | 15.0 | 13.9 | 10.7 | 10.6 | 9.4 | 7.0 | 7.0 | 7.0 | 7.3 | 9.0 | 6.0 | 2 | ||
| 4340.5 | .. | 16.0 | 14.3 | 12.2 | 14.6 | 13.2 | 10.8 | 9.2 | 9.4 | 9.0 | 8.7 | 8.4 | 9.2 | 9.6 | 9.0 | 3 | ||
| 4861.3 | 15.0 | 14.0 | 14.0 | 14.6 | 13.3 | 12.3 | 11.0 | 9.0 | 8.5 | 7.6 | 6.6 | 5.6 | 5.1 | 6.7 | 4.0 | 4 | ||
| He | 4713.4 | .. | .. | .. | .. | 6.5 | 8.2 | 7.5 | 6.0 | 6.7 | 4.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1 | |
| 4713.1 | ||||||||||||||||||
| 4121.0 | .. | .. | .. | .. | 8.5 | 9.5 | 11.0 | 9.2 | 6.4 | 4.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2 | ||
| 4120.9 | ||||||||||||||||||
| 4471.7 | .. | 6.5 | 8.5 | 8.0 | 11.0 | 11.5 | 11.6 | 11.8 | 11.1 | 9.7 | 8.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3 | ||
| 4471.5 | ||||||||||||||||||
| 4026.4 | 4.0 | 6.9 | 9.0 | 8.0 | 12.0 | 12.7 | 14.0 | 15.4 | 12.0 | 10.8 | 8.5 | 0.0 | 0.0 | 0.0 | 0.0 | 4 | ||
| 4026.2 | ||||||||||||||||||
| 4921.9 | .. | .. | .. | .. | 10.0 | 12.4 | 10.7 | 10.0 | 10.0 | 7.0 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5 | ||
| 4387.9 | .. | .. | 4.0 | 4.0 | 10.0 | 10.3 | 11.0 | 11.5 | 9.2 | .. | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6 | ||
| 4143.8 | .. | .. | 5.0 | 4.0 | 9.6 | 10.0 | 10.7 | 12.0 | 7.5 | 4.9 | 3.5 | 0.0 | 0.0 | 0.0 | 0.0 | 7 | ||
| 4009.3 | .. | .. | .. | .. | 7.0 | 9.1 | 10.2 | 11.4 | 5.8 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 8 | ||
| He+ | 4685.8 | em. | 5.8 | em. | 6.0 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9 | |
| 4541.6 | 6.0 | 5.3 | 5.5 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 10 | ||
| 4199.9 | 5.0 | 3.5 | 6.1 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 11 | ||
| 4025.6 | 4.0 | 6.9 | 9.0 | 8.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 12 | ||
| C+ | 4267 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 7.4 | 7.7 | 8.0 | 7.8 | 4.5 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1[Pg 122] | |
| Mg | 5183.7 | |||||||||||||||||
| 5172.7 | .. | .. | .. | .. | .. | 8.0 | .. | .. | 8.0 | 8.0 | 8.0 | 10.0 | 8.0 | 10.0 | .. | 1 | ||
| 5167.4 | ||||||||||||||||||
| 4571.1 | .. | .. | .. | .. | 2.0 | 3.5 | 5.2 | 3.3 | 6.4 | 5.8 | 6.2 | 6.8 | 6.9 | 7.0 | 6.1 | 2 | ||
| 4351.9 | .. | 2.0 | 4.0 | 5.0 | 4.3 | 6.3 | 7.4 | 5.0 | 7.3 | 8.1 | 8.0 | 7.0 | 8.1 | 8.6 | 9.0 | 3 | ||
| Mg+ | 4481.3 | 5.0 | 4.6 | 6.0 | 5.5 | 6.7 | 8.0 | 7.2 | 8.1 | 8.3 | 8.6 | 9.0 | 7.7 | 8.0 | 9.4 | 7.6 | 4 | |
| 4481.1 | ||||||||||||||||||
| Al | 3961.3 | .. | tr. | 2.0 | 5.3 | .. | 5.7 | 5.5 | .. | 8.3 | 8.0 | 8.5 | .. | .. | 9.0 | 11.0 | 1 | |
| 3944.0 | .. | tr. | 2.0 | 6.0 | .. | 5.2 | 6.0 | 8.0 | 8.0 | 8.3 | 8.5 | .. | .. | 8.5 | 11.0 | 2 | ||
| Si | 3905 | .. | .. | 2.0 | .. | 4.0 | 8.8 | 9.3 | 11.5 | 11.7 | 11.4 | 11.3 | 10.0 | 10.0 | 9.6 | 8.6 | 1 | |
| Si+ | 4131 | .. | .. | .. | .. | 2.0 | 3.0 | 2.7 | 3.5 | 4.4 | 3.6 | 6.2 | 9.3 | 7.0 | .. | .. | 2 | |
| 4128 | .. | .. | .. | .. | 2.0 | 3.0 | 2.7 | 3.5 | 4.4 | 3.6 | 6.2 | 9.3 | 7.0 | .. | .. | |||
| Si++ | 4574 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 8.0 | 8.0 | 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3 | |
| 4568 | 0.0 | 0.0 | 0.0 | 0.0 | 2.0 | 9.0 | 9.0 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4 | ||
| 4552 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 10.0 | 10.0 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5 | ||
| Si+++ | 4116 | .. | .. | 5.0 | 6.0 | 8.3 | 4.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6 | |
| 4096 | .. | .. | 8.7 | 6.0 | 9.7 | 5.2 | 3.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7 | ||
| 4089 | .. | .. | 7.5 | 8.0 | 9.2 | 5.5 | 5.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 8 | ||
| Ca | 4581.4 | 0.0 | 0.0 | 0.0 | 3.0 | 2.5 | 4.2 | 6.7 | 5.0 | 7.7 | 8.1 | 7.8 | 8.0 | 7.1 | 8.3 | 6.2 | 1 | |
| 4454.8 | 0.0 | 0.0 | 0.0 | 3.0 | 5.0 | 2.6 | 5.0 | 6.2 | 6.0 | 5.1 | 5.0 | 4.8 | 4.4 | 5.6 | 5.0 | 2 | ||
| 4434.9 | 0.0 | 0.0 | 0.0 | 4.0 | 4.3 | 5.2 | 6.2 | 6.0 | 7.5 | 7.6 | 7.9 | 9.2 | 8.8 | 9.7 | 9.3 | 3[Pg 123] | ||
| 4307.7 | 0.0 | 3.3 | 3.0 | 4.4 | 3.6 | 4.9 | 6.5 | 7.2 | 9.5 | 8.6 | 8.6 | 10.3 | 10.5 | 12.0 | 13.1 | 4 | ||
| 4302.5 | 0.0 | 0.0 | 0.0 | .. | 8.0 | .. | 3.5 | .. | .. | 5.5 | .. | 4.0 | 4.5 | 5.0 | 8.0 | 5 | ||
| 4299.0 | 0.0 | 0.0 | 3.0 | 5.2 | 5.0 | 6.8 | 7.4 | 6.5 | 6.6 | 8.0 | 8.0 | 8.6 | 7.9 | .. | 6.0 | 6 | ||
| 4289.4 | 0.0 | 0.0 | 3.0 | 4.4 | 4.6 | 7.6 | 7.8 | 6.7 | 8.2 | 7.4 | 7.7 | 8.6 | 9.3 | 11.4 | 10.5 | 7 | ||
| 4283.0 | 0.0 | 0.0 | 0.0 | .. | 5.0 | 3.0 | .. | .. | 4.0 | 5.0 | 6.1 | 5.0 | 6.0 | 8.0 | 4.4 | 8 | ||
| 4226.7 | 3.0 | 2.3 | 3.0 | 5.8 | 6.3 | 7.9 | 9.3 | 8.6 | 10.4 | 9.7 | 11.7 | 13.6 | 14.5 | 14.2 | 16.0 | 9 | ||
| Ca+ | 3968.5 | 20.0 | 17.6 | 20.0 | 15.6 | 15.0 | 17.2 | 17.8 | 20.0 | 18.0 | 20.0 | 24.5 | .. | .. | 30.0 | .. | 10 | |
| 3933.7 | 5.0 | 10.3 | 13.3 | 13.8 | 15.0 | 17.1 | 20.0 | 20.0 | 19.6 | 20.0 | 21.5 | .. | .. | 30.0 | .. | 11 | ||
| Sc+ | 4246.8 | 0.0 | 3.0 | 2.0 | 6.0 | 5.0 | 6.0 | 7.0 | 5.0 | 6.3 | 5.6 | 5.3 | 5.6 | 5.4 | 8.6 | 6.8 | 1 | |
| 4320.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.8 | 5.5 | 4.0 | 4.0 | 3.5 | 3.8 | 4.5 | 4.0 | 5.0 | 4.0 | 2 | ||
| Ti | 4395.2 | 0.0 | 0.0 | 0.0 | 3.0 | .. | 6.7 | 7.2 | .. | 5.7 | 5.7 | 5.4 | 6.2 | 6.8 | 7.2 | 6.5 | 1 | |
| 4301.1 | 0.0 | 0.0 | 0.0 | 0.0 | 8.0 | .. | 3.5 | .. | .. | 5.5 | .. | 4.0 | 4.5 | 5.0 | 8.0 | 2 | ||
| 4300.9 | 0.0 | 3.0 | 3.0 | .. | .. | 6.0 | 7.6 | 7.0 | 5.0 | 6.5 | 5.0 | 8.0 | 5.6 | 10.3 | 13.0 | 3 | ||
| 4298.7 | 0.0 | 0.0 | 3.0 | 5.2 | 5.0 | 6.8 | 7.4 | 6.5 | 6.6 | 8.0 | 8.0 | 8.6 | 7.9 | .. | 6.0 | 4 | ||
| 4290.9 | 0.0 | 0.0 | 3.0 | 4.4 | 4.6 | 7.6 | 7.8 | 6.7 | 8.2 | 7.4 | 7.7 | 8.6 | 9.3 | 11.4 | 10.5 | 5 | ||
| 4289.1 | ||||||||||||||||||
| 4274.6 | 0.0 | 0.0 | 1.0 | 3.0 | 0.0 | 3.5 | 5.2 | 5.0 | 6.2 | 7.2 | 7.6 | 9.0 | 8.4 | 9.5 | 9.4 | 6 | ||
| 3998.7 | 0.0 | 0.0 | 1.5 | 4.5 | 6.0 | 5.6 | 7.0 | 6.0 | 7.0 | 7.0 | 6.5 | .. | 7.0 | 8.0 | .. | 7 | ||
| Ti+ | 4571.9 | 0.0 | 0.0 | 0.0 | 0.0 | 2.0 | 3.5 | 5.2 | 3.3 | 6.4 | 5.8 | 6.2 | 6.8 | 6.9 | 7.0 | 6.1 | 8 | |
| 4563.8 | 0.0 | 0.0 | 0.0 | 0.0 | 2.0 | 2.5 | 5.2 | 3.3 | 6.6 | 6.4 | 6.7 | 7.2 | 6.9 | 7.0 | 5.6 | 9 | ||
| 4501.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 6.6 | 5.3 | 6.8 | 6.0 | 6.4 | 6.8 | 7.0 | 6.6 | 6.0 | 10 | ||
| 4443.8 | 0.0 | 0.0 | 0.0 | 5.0 | 8.0 | 6.9 | 8.1 | 7.8 | 7.5 | 7.6 | 7.9 | 9.2 | 8.6 | 8.0 | 9.0 | 11 | ||
| 4395.0 | 0.0 | 0.0 | 0.0 | 3.0 | .. | 6.7 | 7.2 | .. | 5.7 | 5.7 | 5.4 | 6.2 | 6.8 | 6.0 | 6.5 | 12[Pg 124] | ||
| 4337.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 6.3 | 5.0 | 7.2 | 7.8 | 7.2 | 7.2 | 8.9 | 9.0 | 8.3 | 13 | ||
| 4315.0 | 0.0 | 3.0 | 3.5 | 5.0 | 4.6 | 6.9 | 7.5 | 4.6 | 6.6 | 5.6 | 6.1 | 7.0 | 7.0 | 8.0 | 8.1 | 14 | ||
| 4307.9 | 0.0 | 3.3 | 3.0 | 4.4 | 3.6 | 4.9 | 6.5 | 7.2 | 9.5 | 8.6 | 8.6 | 10.3 | 10.5 | 12.0 | 13.1 | 15 | ||
| 4301.9 | 0.0 | 0.0 | 0.0 | 0.0 | 8.0 | .. | 3.5 | .. | .. | 5.5 | .. | 4.0 | 4.5 | 5.0 | 8.0 | 16 | ||
| 4300.0 | 0.0 | 3.0 | 3.0 | .. | .. | 6.0 | 7.6 | 7.0 | 5.0 | 6.5 | 5.0 | 8.0 | 5.6 | 10.0 | 13.0 | 17 | ||
| 4290.2 | 0.0 | 0.0 | 3.0 | 4.4 | 4.6 | 7.6 | 7.8 | 6.7 | 8.2 | 7.4 | 7.7 | 8.6 | 9.3 | 11.0 | 10.5 | 18 | ||
| V | 4395.2 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 6.7 | 7.2 | .. | 5.7 | 5.7 | 5.4 | 6.2 | 6.8 | 7.2 | 6.5 | 1 | |
| 4379.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 2.5 | 3.0 | 3.7 | 2.5 | 2.8 | 3.5 | 3.0 | 4.0 | 4.2 | 2 | ||
| 4332.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | .. | .. | 4.5 | 5.0 | 4.5 | 5.0 | 4.0 | 5.0 | 4.2 | 3 | ||
| 4330.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.5 | 5.0 | 4.5 | 4.5 | 4.0 | 3.5 | 3.8 | 4 | ||
| Cr | 4359.8 | 0.0 | 2.0 | .. | 3.0 | .. | 3.6 | 5.6 | 5.0 | 6.8 | 6.2 | 6.3 | 6.8 | 7.1 | 6.0 | 6.6 | 1 | |
| 4351.9 | 0.0 | 2.0 | 4.0 | 5.0 | 4.3 | 6.3 | 7.4 | 5.0 | 7.3 | 8.1 | 8.0 | 7.0 | 8.1 | 8.0 | 9.0 | 2 | ||
| 4289.7 | 0.0 | 0.0 | 3.0 | 4.4 | 4.6 | 7.6 | 7.8 | 6.7 | 8.2 | 7.4 | 7.7 | 8.6 | 9.3 | 11.4 | 10.5 | 3 | ||
| 4274.9 | 0.0 | 0.0 | 1.0 | 3.0 | .. | 3.5 | 5.2 | 5.0 | 6.2 | 7.2 | 7.6 | 9.0 | 8.4 | 9.5 | 9.4 | 4 | ||
| 4254.4 | 0.0 | 0.0 | 0.0 | 2.5 | 4.0 | 3.3 | 4.6 | 5.0 | 6.4 | 8.0 | 8.0 | 8.6 | 8.6 | 9.5 | 9.9 | 5 | ||
| Mn | 4451.6 | 0.0 | 2.0 | 3.0 | .. | 3.0 | 2.0 | .. | .. | 6.0 | 4.0 | 3.5 | 5.0 | .. | 5.0 | 5.0 | 1 | |
| 4414.9 | 3.0 | 2.3 | 3.3 | 4.8 | 4.6 | 6.4 | 8.0 | 7.2 | 7.0 | 6.5 | 7.2 | 7.6 | 7.4 | 7.0 | 8.0 | 2 | ||
| 4041.4 | 0.0 | 0.0 | 0.0 | 2.5 | 2.0 | 1.9 | 5.2 | 3.5 | 6.0 | 4.8 | 4.8 | 5.5 | 6.0 | 6.0 | 6.0 | 3 | ||
| 4036.5 | 0.0 | .. | .. | .. | .. | .. | .. | .. | .. | 3.3 | 4.0 | .. | .. | .. | .. | 4 | ||
| 4034.5 | 0.0 | .. | .. | .. | .. | .. | .. | .. | 5.0 | 3.6 | 4.0 | .. | 6.0 | .. | .. | 5 | ||
| 4033.1 | 0.0 | .. | .. | .. | .. | .. | 5.0 | 6.0 | 6.0 | 4.3 | 5.0 | .. | 7.0 | .. | .. | 6 | ||
| 4030.8 | 0.0 | 2.0 | 1.0 | 3.6 | 4.0 | 4.0 | 5.7 | 5.5 | 7.0 | 5.4 | 6.4 | 7.0 | 8.0 | 8.5 | 8.0 | 7 | ||
| 4068 | unclas. | .. | .. | .. | 4.3 | .. | 4.3 | 7.6 | 5.0 | 6.6 | 5.7 | 5.8 | 8.0 | 8.5 | 6.0 | 5.5 | 8 | |
| 4092 | unclas. | .. | .. | .. | 3.0 | .. | .. | .. | 3.0 | 4.0 | 4.2 | 4.2 | 5.0 | 5.0 | 6.0 | 5.5 | 9[Pg 125] | |
| Fe | 4489.7 | 0.0 | 0.0 | 2.0 | 0.0 | 0.0 | 4.2 | 7.2 | 6.3 | 6.8 | 6.8 | 7.6 | 8.4 | 7.4 | 8.0 | 7.6 | 1 | |
| 4482.3 | 0.0 | 4.0 | 4.6 | 6.0 | 5.5 | 6.7 | 8.0 | 7.2 | 8.1 | 8.3 | 8.6 | 9.0 | 7.7 | 8.0 | 7.6 | 2 | ||
| 4461.7 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 2.0 | 4.2 | 5.0 | 6.0 | 6.0 | 6.0 | 6.3 | 6.5 | 7.0 | 7.0 | 3 | ||
| 4375.9 | 0.0 | 0.0 | 2.5 | 4.4 | 5.5 | 6.7 | 7.1 | .. | 7.8 | 6.7 | 6.9 | .. | 8.0 | 7.0 | 8.8 | 4 | ||
| 4216.1 | 0.0 | 2.0 | 1.5 | 3.8 | 3.3 | 5.6 | 6.6 | 2.6 | 8.6 | 7.3 | 8.5 | 9.4 | 8.1 | 8.0 | 7.9 | 5 | ||
| 4415.1 | 3.0 | 2.3 | 3.3 | 4.8 | 4.6 | 6.4 | 8.0 | 7.2 | 7.0 | 6.5 | 7.2 | 7.6 | 7.4 | 7.0 | 8.0 | 6 | ||
| 4404.7 | 0.0 | 0.0 | 0.0 | 0.0 | 6.0 | 4.4 | 6.7 | 5.0 | 6.1 | 7.4 | 7.8 | 8.8 | 8.0 | 8.0 | 9.1 | 7 | ||
| 43834 | 3.0 | 2.5 | 4.0 | 5.4 | 4.6 | 6.7 | 7.0 | 8.2 | 9.1 | 10.3 | 10.3 | 10.5 | 9.9 | 11.0 | 10.3 | 8 | ||
| 4337.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 6.3 | 5.0 | 7.2 | 7.8 | 7.2 | 7.2 | 8.9 | 9.0 | 8.3 | 9 | ||
| 4291.4 | 0.0 | 0.0 | 3.0 | 4.4 | 4.6 | 7.6 | 7.8 | 6.7 | 8.2 | 7.4 | 7.7 | 8.6 | 9.3 | 11.0 | 10.5 | 10 | ||
| 4325.8 | 0.0 | 0.0 | 3.5 | 5.5 | 3.3 | 6.3 | 7.8 | 9.0 | 10.0 | 11.0 | 11.3 | 11.7 | 10.9 | 11.0 | 10.2 | 11 | ||
| 4307.9 | 0.0 | 3.3 | 3.0 | 4.0 | 3.6 | 4.9 | 6.5 | 7.2 | 9.5 | 8.6 | 8.6 | 10.3 | 10.5 | 12.0 | 13.1 | 12 | ||
| 4271.8 | 0.0 | 2.3 | 2.5 | 4.2 | 4.5 | 4.5 | 6.5 | 6.3 | 7.2 | 8.3 | 8.6 | 9.2 | 8.7 | 10.0 | 9.1 | 13 | ||
| 4260.5 | 0.0 | 3.0 | 1.5 | 4.2 | 4.0 | .. | 5.5 | 6.6 | 7.0 | 8.0 | 8.8 | 9.0 | 8.1 | 10.0 | 9.0 | 14 | ||
| 4290.8 | 0.0 | 0.0 | 2.0 | 3.6 | 4.0 | 5.6 | 5.3 | 6.3 | 6.4 | 7.8 | 7.9 | 8.4 | 8.0 | 9.0 | 7.6 | 15 | ||
| 4143.9 | 0.0 | 2.0 | 2.5 | 4.4 | 3.3 | 4.8 | 6.1 | 5.7 | 7.7 | 7.7 | 8.9 | 8.6 | 8.5 | 11.0 | 10.0 | 16 | ||
| 4132. | 0.0 | 3.6 | 2.0 | 4.0 | 2.0 | 4.2 | 6.0 | 4.0 | 6.0 | 5.2 | 5.5 | 6.0 | 6.5 | 5.0 | 4.0 | 17 | ||
| 4071.7 | 0.0 | 2.0 | 2.0 | 4.0 | 3.0 | 4.3 | 6.6 | 5.7 | 7.8 | 7.5 | 9.2 | 9.0 | 9.0 | 9.5 | 8.6 | 18 | ||
| 4063.6 | 0.0 | 2.0 | 2.0 | 3.6 | 4.0 | 4.8 | 5.8 | 5.6 | 7.2 | 7.5 | 8.0 | 9.0 | 8.0 | 9.5 | 9.0 | 19 | ||
| 4045.8 | 0.0 | 2.0 | 2.5 | 4.6 | 5.0 | 5.6 | 6.9 | 7.6 | 8.8 | 9.2 | 10.3 | 10.6 | 8.6 | 11.0 | 10.8 | 20 | ||
| 4005.2 | 0.0 | 0.0 | 2.5 | 4.6 | 5.5 | 5.0 | 6.3 | 6.0 | 8.3 | 7.2 | 6.6 | 9.0 | 8.0 | 7.0 | .. | 21 | ||
| 4299.2 | 0.0 | 3.0 | 3.0 | .. | .. | 6.0 | 7.6 | 7.0 | 5.0 | 6.5 | 5.0 | 8.0 | 5.6 | 10.3 | 13.0 | 22 | ||
| 4271.2 | 0.0 | 2.3 | 2.5 | 4.2 | 4.5 | 4.2 | 6.5 | 6.3 | 7.2 | 8.3 | 8.6 | 9.2 | 8.7 | 10.0 | 9.1 | 23 | ||
| 4260.5 | 0.0 | 3.0 | 1.5 | 4.2 | 4.0 | .. | 5.5 | 6.6 | 7.0 | 8.0 | 8.0 | 9.0 | 8.1 | 8.5 | 9.0 | 24 | ||
| 4250.1 | 0.0 | 0.0 | 2.0 | 3.6 | 4.0 | 5.6 | 5.3 | 6.3 | 6.4 | 7.8 | 7.9 | 8.4 | 8.0 | 9.0 | 7.6 | 25 | ||
| 4187.8 | 0.0 | 0.0 | 2.0 | 5.0 | 6.0 | .. | .. | .. | 6.0 | 5.5 | 6.0 | .. | .. | .. | 8.0 | 26 | ||
| 4482.3 | 0.0 | 4.0 | 4.6 | 6.0 | 5.5 | 6.7 | 8.0 | 7.2 | 8.1 | 8.3 | 8.6 | 9.0 | 7.7 | 8.0 | 7.6 | 27 | ||
| 4408.4 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 3.5 | 5.7 | 4.0 | 5.6 | 6.0 | 6.0 | 8.0 | 7.9 | 7.0 | 9.0 | 28[Pg 126] | ||
| 4352.7 | 0.0 | 2.0 | 4.0 | 5.0 | 4.3 | 6.3 | 7.4 | 5.0 | 7.3 | 8.1 | 8.0 | 7.0 | 8.1 | 8.0 | 9.0 | 29 | ||
| 4315-1 | 0.0 | 3.0 | 3.5 | 5.0 | 4.6 | 6.9 | 7.5 | 4.6 | 6.6 | 5.6 | 6.1 | 7.0 | 7.0 | 8.0 | 8.1 | 30 | ||
| 4282.4 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 3.0 | .. | .. | 4.0 | 5.0 | 6.1 | 5.0 | 6.0 | 8.0 | 4.4 | 31 | ||
| 4258.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 4.8 | .. | 4.5 | 5.2 | 4.3 | 4.5 | 5.3 | 10.0 | 4.0 | 32 | ||
| 4216.2 | 0.0 | 2.0 | 1.5 | 3.8 | 3.3 | 5.6 | 6.6 | 2.6 | 8.6 | 7.3 | 8.5 | 9.4 | 8.1 | 9.5 | 7.9 | 33 | ||
| 4134.3 | 0.0 | 0.0 | 0.0 | 3.0 | 2.0 | 4.0 | 3.5 | 4.5 | 5.5 | 5.2 | 5.6 | 7.0 | 7.0 | 5.0 | 5.5 | 34 | ||
| 3953 | unclas. | 0.0 | 0.0 | 2.0 | 5.3 | .. | 5.7 | 5.5 | .. | 8.0 | 8.0 | 7.5 | .. | .. | .. | .. | 35 | |
| 3999 | unclas. | 0.0 | 0.0 | 1.5 | 4.5 | 6.0 | 5.6 | 7.0 | 6.0 | 7.6 | 7.0 | 6.5 | .. | 7.0 | 8.0 | .. | 36 | |
| 4172 | unclas. | 0.0 | 2.0 | 3.0 | 4.6 | 4.6 | 6.3 | 9.0 | 5.7 | 7.3 | 5.8 | 6.4 | 7.3 | 6.0 | 9.0 | 8.2 | 37 | |
| 4401 | unclas. | 0.0 | 0.0 | 0.0 | 3.0 | 6.0 | 6.6 | 8.0 | 6.2 | 6.8 | 6.0 | 5.5 | 6.2 | 6.9 | 6.0 | 6.5 | 38 | |
| 4462 | unclas. | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 2.0 | 4.2 | 5.0 | 6.0 | 6.0 | 6.0 | 6.3 | 6.5 | 7.2 | 7.0 | 39 | |
| 4476 | unclas. | 0.0 | 0.0 | 0.0 | 3.0 | 5.0 | 5.2 | .. | .. | 6.3 | 4.0 | 4.1 | 4.0 | 4.3 | 7.5 | 4.7 | 40 | |
| Fe+ | 4173.3 | 0.0 | 2.0 | 3.0 | 4.6 | 4.6 | 6.3 | 9.0 | 5.7 | 7.3 | 5.8 | 6.4 | 7.3 | 6.0 | 8.0 | 8.2 | 41 | |
| 4178.8 | 0.0 | 0.0 | 2.5 | 4.3 | .. | 6.8 | 9.1 | .. | 6.0 | .. | .. | .. | .. | .. | 6.5 | 42 | ||
| 4416.8 | 0.0 | 2.3 | 3.3 | 4.8 | 4.6 | 6.4 | 8.0 | 7.2 | 7.0 | 6.5 | 7.2 | 7.6 | 7.4 | 7.0 | 8.0 | 43 | ||
| Zn | 4810.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | tr | .. | tr | 1 | tr | 0 | .. | 0 | .. | .. | 1 | |
| 4722.2 | 0.0 | 0.0 | 0.0 | 0.0 | tr | tr | .. | tr | 1 | tr | 1- | .. | 1- | .. | .. | 2 | ||
| Sr | 4607.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.0 | 4.0 | .. | 7.0 | .. | 8.5 | 8.0 | 8.7 | 9.0 | 9.2 | 1 | |
| Sr+ | 4215.5 | .. | 2.0 | 1.5 | 3.8 | 3.3 | 5.6 | 6.6 | 2.6 | 8.6 | 5.3 | 8.5 | 9.4 | 8.1 | 8.0 | 7.9 | 2 | |
| 4077.7 | .. | 4.2 | 2.5 | 4.2 | 5.0 | 6.9 | 8.4 | 8.6 | 9.2 | 7.8 | 9.5 | 9.3 | 8.3 | 11.0 | 10.8 | 3 | ||
| Y+ | 4374.9 | 0.0 | 0.0 | 2.5 | 2.4 | 5.5 | 6.7 | 7.1 | .. | 7.8 | 6.7 | 6.9 | .. | 8.0 | 8.8 | 9.6 | 1 | |
| 4177.5 | 0.0 | 0.0 | 2.5 | 4.3 | .. | 6.8 | 9.1 | .. | 6.0 | .. | .. | .. | .. | .. | 6.5 | 2 | ||
| 4398. | .. | .. | .. | .. | .. | .. | .. | .. | 7.0 | .. | .. | 4.0 | 2.6 | 2.0 | 3.7 | 3 | ||
| Ba+ | 4554 | 0.0 | 0.0 | 2.0 | .. | .. | 4.0 | 4.7 | .. | 3.5 | 3.0 | 4.6 | 4.8 | 5.5 | 5.5 | 5.6 | 1[Pg 127] |
NOTES TO TABLE XIX
| Atom | Note | Max. | Blends | Remarks |
|---|---|---|---|---|
| H | 1 | .. | No measures available across the whole
range of these lines. They are blended with He+ in the |
|
| 2 | .. | |||
| 3 | .. | |||
| 4 | .. | |||
| He | 1,2,3, 4 5,6,7,8 | .. | Maximum well determined. Unblended | |
| 4 | He+ | See Note 12 | ||
| 9,10,11,12 | Probably blended. See H. C. 263, 1924 | |||
| C | 1 | .. | Unblended | |
| Mg | 1 | .. | Effectively unblended. Material very meager | |
| 2 | .. | Unblended | ||
| 3 | none | Cr probably predominates | ||
| 4 | -, |
Fe predominates at lower temperature; Mg probably responsible for maximum | ||
| Al | 1 | none | .. | |
| 2 | none | .. | ||
| Si | 1 | -2; -1; |
Si predominates, and is responsible for maximum | |
| 2 | ||||
| 34,5 | .. | |||
| 6 | .. | |||
| 7 | N++ | |||
| 8 | ||||
| Ca | 1 | Ca probably responsible for rise at
|
||
| 2 | Ca, |
Ca probably predominates. Enhanced
line suspected near |
||
| 3 | Calcium predominates. Enhanced
line suspected near |
|||
| 4 | none | In |
||
| 5 | none | Maximum undetermined. In |
||
| 6 | Fe probably responsible for maximum | |||
| 7 | Chromium (ultimate) line probably
obliterates the Ca line. Maximum at |
|||
| 8 | ||||
| 9 | none | Unblended | ||
| 10 | ? | Hydrogen predominates before |
||
| 11 | ? | Unblended | ||
| Sc | 1 | Y? |
Sc predominates, at least at maximum | |
| 2 | Sc predominates | |||
| Ti | 1 | Blended with Ti+. See Note 10 | ||
| 2 | (none) | Ca causes rise at |
||
| 3 | Ti+ causes rise at |
|||
| 4 | ||||
| 5 | ( |
Ca and Cr cause rise at |
||
| 6 | (none) | Cr (ultimate) line predominates | ||
| 7 | none | Possibly an enhanced line accounts
for maximum near |
||
| 8 | Mg accounts for maximum at |
|||
| 9 | Unblended | |||
| 10 | Ti, -5 | Probably unblended | ||
| 11 | Maximum at |
|||
| 12 | Blended with Ti. See Note 1 | |||
| 13 | ? | Fe predominates. Maximum uncertain | ||
| 14 | Rise at |
|||
| 15 | Rowland gives no Ti. Other lines account
for later maximum. In |
|||
| 16 | ? | Maximum undetermined. In |
||
| 17 | Unblended | |||
| 18 | Cr accounts for strength in |
|||
| V | 1 | Ti and Ti+ lines blended. V probably obliterated | ||
| 2 | none | Unblended | ||
| 3 | none | Ti, |
V probably effective at low temperatures, as these are the ultimate lines | |
| 4 | none | |||
| Cr | 1 | Unblended | ||
| 2 | none | Unblended | ||
| 3 | none | Cr probably predominates | ||
| 4 | none | Cr predominates | ||
| 5 | none | Unblended | ||
| Mn | 1 | none | Unblended | |
| 2 | none | Fe predominates? | ||
| 3 | none | |||
| 4 | none | Mn predominates | ||
| 5 | none | Mn-Fe |
||
| 6 | none | Fe-Mn |
[Pg 129] | |
| 7 | Fe, |
Mn predominates? | ||
| 8 | Fe-Mn 6 | |||
| 9 | ||||
| Fe | 1 | Mn-Fe | Effectively unblended | |
| 2 | ( |
No. 2 the weaker line, Mn+ affects
the line at and before |
||
| 3 | none | Fe-Mn, 3 |
Effectively unblended | |
| 4 | none | Sc, Fe? 3; |
Y+ accounts for maximum at |
|
| 5 | - | Sr+ | Due entirely to Sr+ | |
| 6 | Maximum at |
|||
| 7 | Unblended | |||
| 8 | Unblended | |||
| 9 | ( |
Ti+ ( |
||
| 10 | ( |
Ti predominates? | ||
| 11 | Fe probably predominates | |||
| 12 | none | Ca produces rise in late classes? | ||
| 13 | Unblended. Rise at |
|||
| 14 | Fe |
Unblended. Rise at |
||
| 15 | Rise at |
|||
| 16 | ||||
| 17 | Maximum at |
|||
| 18 | ||||
| 19 | ||||
| 20 | Fe predominates | |||
| 21 | ||||
| 22 | Rise at |
|||
| 23 | No. 23 the weaker line | |||
| 24 | No. 24 the strongest line | |||
| 25 | See No. 15. Rise at |
|||
| 26 | ? | |||
| 27 | The stronger line. Responsible also for the maximum of line 2 | |||
| 28 | Rise at |
|||
| 29 | none | Cr and Mn predominate. Cr (ultimate)
line responsible for rise at |
||
| 30 | Maximum at |
|||
| 31 | Ca produces rise at |
|||
| 32 | Rise at |
|||
| 33 | Sr+ | Due entirely to Sr+ | ||
| 34 | ||||
| 35 | ? | Too heavily blended | ||
| 36 | Co |
Maximum at |
||
| 37 | Cr, La, Mn, Ni, |
See Rowland, p. 37. An Fe+ line responsible | ||
| 11 | ||||
| 39 | none | Rise at |
||
| 40 | ( |
Rise at |
||
| 41 | Maximum certainly due to Fe+. Neutral Fe causes rise in cool classes | |||
| 42 | Maximum due to ionized iron | |||
| 43 | Maximum due to Fe+; later rise perhaps due to Mn | |||
| Zn | 1 | Unblended | ||
| 2 | Unblended | |||
| Sr | 1 | none | Fe probably predominates, except perhaps at the lowest temperatures | |
| 2 | Fe probably strong, but Sr responsible
for part of maximum at |
|||
| 3 | Fe, |
Maximum uncertain owing to heavy blending | ||
| Y | 1 | Y+ gives the maximum | ||
| 2 | Maximum ill determined, but probably due to Y+ | |||
| 3 | -1 | Remark in Rowland:--in zircon but not in Zr | ||
| Ba | 1 | none | Unblended |
CONSISTENCY OF RESULTS
The preceding tabulation summarizes the present state of the
observational material bearing on the positions of the maxima of
absorption lines. The comparison with theory is an important and
difficult problem. The theoretical formulae contain as variables the
temperature and the pressure; and the
[Pg 131] fractional concentration,
, is very sensitive to changes in both these variables. It would
therefore be possible to satisfy almost any observations by varying
the two quantities jointly; but this procedure would furnish no useful
test of the theory. The test made in the present chapter will involve
the calculation of the temperature scale, with the partial electron
pressure,
, assumed constant.
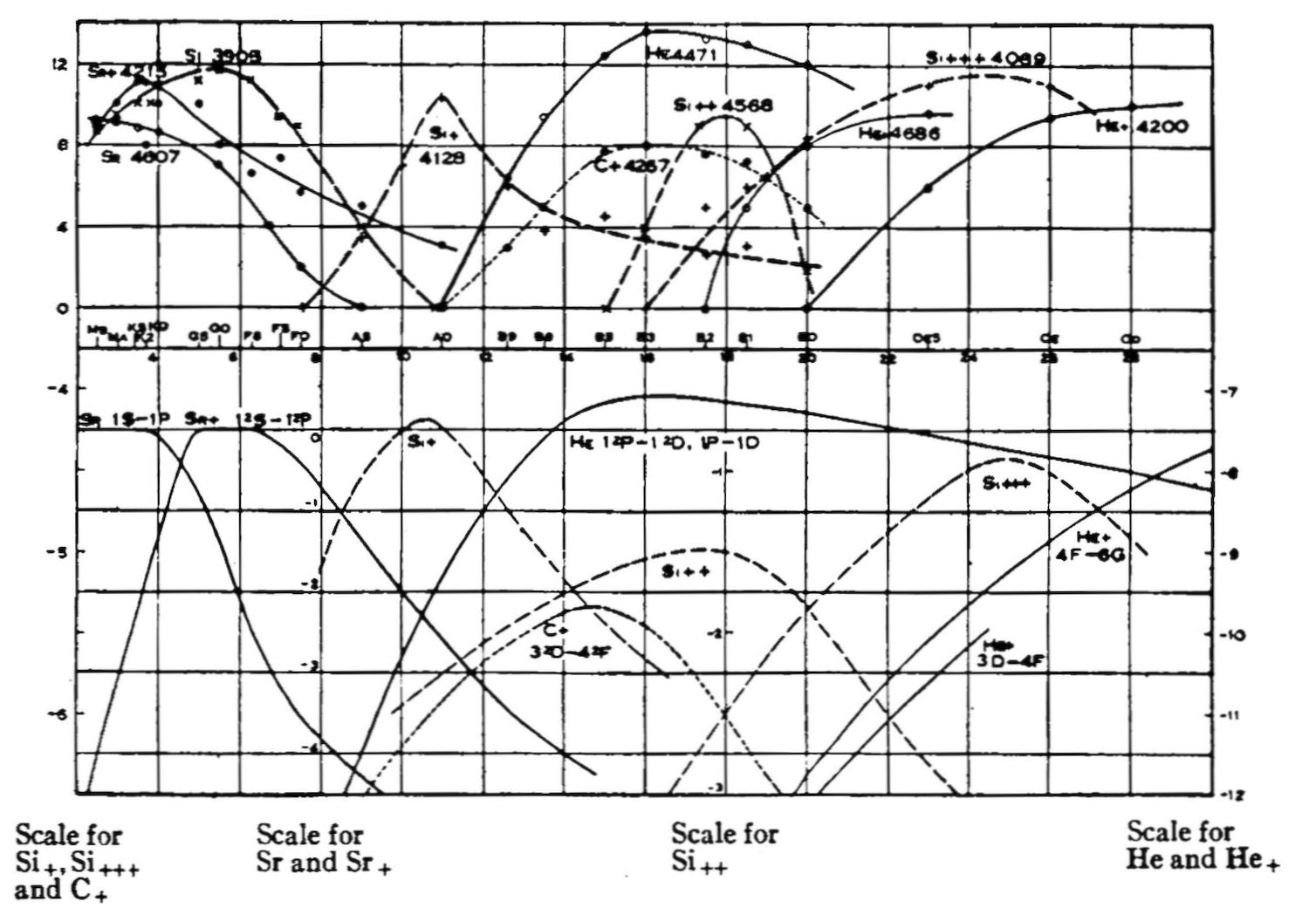
Figure 8
Reproduced from H.C. 256, 1924. Comparison between observation
and ionization theory for the hotter stars. The observations are
contained in the upper part of the diagram, and the theoretical curves
(based on a partial electron pressure
are
given in the lower part of the figure. For the upper half, ordinates
are the observed intensities contained in Table XIX; abscissae are
spectral classes from the Draper Catalogue. In the lower part of the
figure, ordinates are logarithms of computed fractional concentrations;
abscissae are temperatures in thousands of degrees. The abscissae of
the upper and lower diagrams have been adjusted so that the observed
and computed maxima coincide, thus forming a preliminary temperature
scale.
It is certain that this condition is not satisfied in practice,
and a more rigorous treatment, which allows for the differences in
partial electron pressure, is contained in the chapter that follows.
But with the object of examining the consistency of the derived
temperature scale, the present test is made under the assumption that
the partial electron pressure is constant and equal to about
[Pg 132]
.
The resulting scale of temperatures for the reversing layers of the corresponding classes is contained in the table that follows. Successive columns contain the element that is utilized, the spectral class at which its lines attain maximum, and the corresponding temperature derived from the equations of Chapter VII.
| Element | Maximum | Temperature | Element | Maximum | Temperature |
|---|---|---|---|---|---|
| He+ | 35000° | Ti | 3500° | ||
| Si+++ | 25000 | Mn | 5000 | ||
| Si++ | 18000 | Fe | 5000 | ||
| He | 10000 | V | 3500 | ||
| C+ | 16000 | Cr | 3500 | ||
| Si+ | 11000 | Sr+ | 6000 | ||
| H | 10000 | Ba+ | None | 5500 | |
| *Zn | 8000 | Ca | 4500 | ||
| *Ca+ | 6000 |
* Estimates by Menzel, H. C. 258, 1924.
[403] Payne, H. C. 256, 263, 1924.
[404] Menzel, H. C. 258, 1924.
[405] Harper and Young, Pub. Dom. Ap. Obs., 3, 3, 1925.
[407] Menzel, H. C. 258, 1924.
[Pg 133]
A preliminary application of the observed maxima of absorption lines,
in the formation of a stellar temperature scale, was given at the
end of the preceding chapter. The temperatures were obtained on the
assumption that , the partial electron pressure in the reversing
layer, was constant for all lines and equal to
.
Striking inconsistencies appear in this preliminary table of
temperatures. As Menzel[408] has remarked, the maxima of most of the
metallic arc lines occur in stars cooler than the ionization theory,
on the stated assumptions, would predict. The ultimate lines of the
ionized atoms of calcium, strontium, and barium show especially
large inconsistencies. The temperatures of the maxima for these
atoms, deduced from the ionization formula on the assumption that
, are
about 3000° higher than the measured temperatures of the classes at
which the maxima occur, as deduced from the color indices.
The following suggestion has been advanced by Fowler and Milne[409]
to account for the observed deviations of Ca+, Sr+, and Ba+. “For the
maximum of the principal line of an ionized atom, the fraction of atoms
in the required state is almost unity.... On the other hand ... at the
maxima of subordinate lines the fraction of atoms in the required state
is from to
.... Thus atoms in the required
state are
to
times as abundant for intense
principal lines as for intense subordinate lines. It follows that
principal lines must originate at much higher levels in the stellar
atmosphere than subordinate lines, and consequently at much smaller
pressures.”
[Pg 134]
It appears that the behavior of the ionized atoms of the alkaline earths can be satisfactorily explained in this way. The further suggestion was made that a similar effect might be expected for atoms of low excitation potential, such as manganese and magnesium.
The possibility of varying as well as
in the formula
for the theoretical maximum places the investigation on a rather
different footing. Any temperature (within wide limits) may now be
obtained for the theoretical maximum of a line by appropriately varying
the partial pressure. The stellar temperature scale cannot, in such
a case, be fixed merely from a knowledge of the critical potentials
and the observed maxima, without introducing other considerations.
It is necessary to find a way of determining the appropriate partial
pressures.
The procedure that will here be followed consists essentially in a
calibration and an extrapolation. The temperature scale from
to
is regarded as known from spectrophotometric data. Within
this range, the theoretical and observed maxima are compared. The
possibility of finding a value of
appropriate to a given
atomic state is next examined. Finally, a method of estimating
will be justified for the cooler stars, within the limits of accuracy
permitted by the data, and will be extended by simple extrapolation to
the formation of a temperature scale for the hotter stars, where the
temperatures cannot be safely estimated from the color indices.
The salient point is that complete absorption will occur for any line at a depth that is inversely proportional to the abundance of the corresponding state of the atom. No light in this wave-length reaches the exterior from any lower level, and the deepest level from which the line originates therefore forms a lower boundary to the effective portion of the atom in question. The “effective level” from which a line comes is probably best regarded as the level at which the effective atoms above the “lower boundary” have their median frequency. Clearly the partial pressure will differ at different effective levels, and thus abundance has a direct influence on the appropriate value of [Pg 135] the partial pressure.
The theory with which we have so far been concerned deals with the
excited fraction of the total amount of the element which is
present. A knowledge of this quantity suffices for specifying the
variation of intensity for the lines of any one element. But the
absolute abundance of a given atomic state varies jointly with the
fractional concentration of the appropriate state and the total amount
of the element present. Now, for the first time, the absolute abundance
of different atomic species becomes of possible importance, as a
factor affecting the depth from which radiation corresponding to the
given atom will penetrate. Fowler and Milne[410] rightly claimed that
their method of maxima eliminated questions of relative abundance, “if
can be regarded as known ... [and constant]. The proper value
of
must be a function of the abundance of the atom in question
relative to free electrons.”
The question of relative abundances of elements in the reversing layer is discussed[411] in Chapter XIII. It may be mentioned that the abundances there deduced depend upon estimates of marginal appearance. Probably all lines are unsaturated at marginal appearance, that is, there are not enough suitable atoms present completely to absorb all the incident light of the appropriate wave-length. Hence all suitable atoms present, as far down as the photosphere, where general opacity begins to render the gas hazy, are actually contributing to the line. At marginal appearance, then, all the intensity phenomena are probably due to pure abundance, and considerations of level are eliminated. The deduced abundances are therefore independent of effects such as are discussed in the present chapter, and the results of Chapter XIII may be cited as giving evidence that the stellar abundances, for all the atoms here to be considered except barium, have a range with only a factor of ten, which is negligible in comparison with the quantities to be discussed. The relative abundance of [Pg 136] different atomic species will therefore be neglected in what follows, although, with more accurate data than are now available, it should become a factor of importance.
Fractional concentrations, as derived from the ionization formula,
govern the effective level at which absorption takes place. Fowler
and Milne, as was pointed out earlier, suggested that the higher the
fractional concentration at maximum, the higher the level and the lower
the partial pressure from which the line originates. They suggested
that the pressure for a principal line at maximum is from
to
of the corresponding value for a subordinate line.
The assumption now introduced is, in effect, that the absorbing
efficiency of individual atoms is the same. The partial pressure at the
level from which a line originates should then vary inversely as the
fractional concentration at maximum. In other words, the product
should be constant, when
is deduced from the class at which the
observed maximum occurs.
The quantity depends primarily on the excitation
potential, and varies but slowly with
. It is given by the
expression[iii]
[iii] For notation, see Chapter VII, p. 106.
For subordinate lines, is given by the expression
and this quantity is extremely sensitive to change in
.
For ultimate lines, where the excitation potential is equal to zero,
and accordingly reduces to unity, the value of
should be equal to the constant product predicted in a previous
[Pg 137]
paragraph. Fowler and Milne suggested a partial electron pressure
of
to
for Ca+ on the basis of a maximum at
, assumed temperature 4500°. This is the effective temperature
of the class, deduced spectrophotometrically, and “the reversing layer
should be at a lower temperature—its average temperature should be in
the neighborhood of, or somewhat lower than, the Schwarzschild boundary
temperature,[iv] which is some 15-20 per cent lower than the effective
temperature.” The value 4000° is therefore adopted here for
.
For this value
becomes
for Ca+; for
Sr+ (
, 35000°),
, and for Ba+
(Ma? 3000°),
. The maximum for Sr+ is the
best determined of the three, as the Ca+ lines are too strong and too
far into the violet for an accurate estimate among the cooler stars,
and the Ba+ line is rather faint, and is heavily blended. The constant
product may then be expected to be of the order of
.
The prediction is examined in the table that follows. The temperature of the class at which the lines attain maximum is assumed from spectrophotometric data, and is expressed to the nearest five hundred degrees.
| Atom | Ionization Potential |
Excitation Potential |
Max. | |
|
Sum | |
|---|---|---|---|---|---|---|---|
| Mg+ | 14.97 | 8.83 | 9000° | 5.32 | |||
| Ca | 6.09 | 1.88 | 3000 | 3.64 | |||
| Ti | 6.5 | 0.84 | 3500 | 2.7 | |||
| Cr | 6.75 | 0.94 | 3000 | 2.39 | |||
| Mn | 7.41 | 2.16 | 3500 | 3.77 | |||
| Zn | 9.35 | 4.01 | 5600 | 3.0 | |||
| Ca+ | 11.82 | 0.00 | 4000 | 0.00 | |||
| Sr+ | 10.98 | 0.00 | 3500 | 0.00 | |||
| Ba+ | 9.96 | 0.00 | 3000 | 0.00 | |||
| Mg | 7.61 | 2.67 | 4000 | 3.25 |
[iv: The Schwarzschild approximation to the boundary temperature is
given by the expression
[Pg 138]
where
is the effective temperature and
the boundary
temperature.]
Successive columns give the atom, the critical potentials in volts, the
spectral class at which maximum occurs, the assumed ,
calculated from the theory,
, and the
sum of the quantities in the two preceding columns. The only quantity
that is not fixed by the laboratory data is
, which is
derived from the data presented in Chapter II. It will be seen that the
quantity entered in the last column is sensibly constant, and equal to
about -10, in accordance with prediction. All available maxima have
been used.
It appears that the foregoing evidence constitutes a fair and satisfactory test of the Fowler-Milne equations, and that, in the region in which the test can be applied, the agreement with theory is as close as can be expected from the material. It also appears that the “serious and undoubtedly real” discordance of theory and observation, quoted by Menzel in the discussion of the maxima observed by him, is removed by introducing these considerations of level.
When the theory has been applied and justified for the classes where
the temperature scale is well determined by other methods, it may be
extrapolated to fix the temperature scale for the hotter stars. As
before, the fractional concentration at maximum varies but slowly with
, and
is determined mainly by
. If now
be so chosen that
is always approximately
equal to
, the value of
derived from the equations
will be the appropriate one for the class in question. This value of
has to be found by trial. It so happens that the temperatures
thus obtained are not very different from those originally predicted
without entering into considerations of effective level. The excitation
potentials of the highly ionized stages of the lighter elements are
invariably large, and all lead to values of
of the order of
. It is to be noted that values of
greater
than
are not indicated.
The following tabulation represents the resulting temperature scale for
[Pg 139]
the hotter stars. It must be remembered that is here the
derived quantity, whereas in Table XX it was the known quantity
used for calibration.
| Atom | Ionization Potential |
Excitation Potential |
Max. | |
|---|---|---|---|---|
| He+ | 54.2 | 48.2 | 35000° | |
| C+ | 24.3 | 18.0 | l6000 | |
| He | 24.7 | 21.1 | 10000 | |
| Si++ | 31.7 | 4.8 | 18000 | |
| Si+++ | 45.0 | 24.0 | 25000 |
The values given in the preceding table constitute the only contribution that can be made by this form of ionization theory to the formation of a stellar temperature scale. Values assigned to intermediate classes must be conjectural. From the observed changes of intensity from class to class, temperatures may be interpolated roughly, and a temperature scale, formed on these general grounds, is reproduced in Table XXII. Values not derived from observed maxima are italicized.
| Class | Temperature | Class | Temperature | |
|---|---|---|---|---|
| 3000° | 9000° | |||
| 3000 | 10000 | |||
| 3500 | 13500 | |||
| 4000 | 15000 | |||
| 5000 | 17000 | |||
| 5600 | 18000 | |||
| 7000 | 20000 | |||
| 7500 | 25000 | |||
| 8400 | to | 35000 |
[408] H. C. 258, 1924.
[409] M. N. R. A. S., 84, 499, 1924.
[410] M. N. R. A. S., 84, 499, 1924.
[Pg 140]
DIFFERENCES between the spectra of stars of the same spectral class have long been recognized. The empirical correlation of relative line intensities with absolute magnitude was made the basis for the estimation of spectroscopic parallaxes.[412] Such differences within a class were later related in a qualitative way to differences of pressure, in conjunction with the theory of thermal ionization, and have been regarded as corroborative evidence that the type of process contemplated by that theory actually represents what goes on in the atmospheres of the stars.
In the present chapter the theory of the various effects will first be discussed, and later the predictions from the theory will be compared with observational data.
INFLUENCE OF SURFACE GRAVITY ON THE SPECTRUM
The first theoretical discussion of the effects of absolute magnitude
upon the stellar spectrum seems to have been made by Pannekoek,[413]
who pointed out that “stars of the same spectral class ... will show
differences depending solely on ... ,” where
is the
surface gravity, and
the absorption coefficient. Pannekoek
considered all stars of the same spectral class to have the same
temperature, and for the purposes of his argument the differences
in temperature between giants and dwarfs can be neglected, although
actually they may for other reasons have a noticeable effect on the
spectrum. If
be regarded as constant, a plausible assumption for
various reasons,[414] “the physical quantity, directly given by the
spectra used for the determination of spectroscopic parallaxes is the
[Pg 141]
gravitation at the surface of the star.”[415] The relation between the
surface gravity and the pressure is given by
where
is the “homogeneous depth.” The pressure is then
directly proportional to the surface gravity.
INFLUENCE OF PRESSURE ON THE SPECTRUM
Lowered pressure increases the degree of ionization. The tendency of the atoms to lose electrons by thermal ionization should depend solely on their energy supply, and should thus be independent of the pressure. The total absorbing power of the gas will, however, depend on the number of suitable atoms that it contains, not upon their rate of formation. The number of suitable ionized atoms present at any moment in the atmosphere is a function not only of the rate at which ionization proceeds, but also of the rate of recombination. The more readily recombination takes place, the larger is the number of effective neutral atoms, and the smaller the number of effective ionized atoms, when a steady state is attained. The rate of recombination, which depends upon the probability of a suitable encounter between an ionized atom and a free electron, will increase with the pressure—more accurately, with the partial pressure of free electrons.
The higher the pressure, therefore, the greater the number of neutral atoms, and the smaller the number of ionized atoms. This argument explains at once the strength of the neutral (arc) lines in the spectra of stars of low luminosity (high surface gravity), and the predominance of ionized (spark) lines for absolutely bright stars (low surface gravity, resulting chiefly from large radius). Low surface gravity, then, increases the number of ionized atoms present by discouraging recombination.
It should be noted that any tendency to extensive ionization will increase the concentration of free electrons and tend to encourage [Pg 142] recombination, thus counteracting the effect of low surface gravity. The effect of an increased concentration of free electrons will not, however, attain the magnitude of the surface gravity effect, since even for the hottest stars examined, three electrons appear to be the largest number that can be thermally removed under reversing layer conditions.
The theoretical effect of lowering the pressure has been discussed by
Stewart,[416] who, after alluding to the importance of the surface
gravity, suggested that the ultimate lines of neutral atoms easier to
ionize than the average should be weakened by low pressure, and that
the corresponding enhanced lines should be strengthened. For atoms
harder to ionize than the average the reverse should be the case for
the two classes of lines. From this standpoint he showed that the
absolute magnitude effects might be qualitatively accounted for. The
“average ionization potential” was the average for the lines used in
the estimates; Stewart adopted the value of six volts for Classes
to
.
EFFECT OF TEMPERATURE AND DENSITY GRADIENTS UPON THE SPECTRUM OF A STAR
There is another respect, recently analyzed by Stewart,[417] in which the spectrum of a giant may be expected to differ from that of the corresponding dwarf. He points out that “in a giant, owing to the small density, there is more material overlying the photosphere than in a dwarf having the same effective temperature; while at the same time the density in the photospheric region is less in the giant, owing to the low gravity.” These conditions furnish an interpretation of the increased blackness and sharpness of the lines in giant stars, as compared with the corresponding dwarfs. The absorption lines in giants are blacker because there is more matter above the photosphere than in dwarfs; they are sharper because the effective level at which the lines originate is at a lower pressure in the giant than in the dwarf, owing to the smaller pressure gradient in the giant [Pg 143] star, and to its lower surface gravity. The difference in line quality between a giant and a dwarf is at once obvious from the spectra, and this effect renders direct comparisons of estimated line-intensities a matter of extreme difficulty. It is an effect that must be taken into account in examining the agreement between the observations and the theory.
Stewart’s argument also suggests the answer to an important question
raised by Pannekoek[418] in the course of his discussion of the
absolute magnitude effect. The latter remarks that “the general
decrease of luminosity with advancing type for the same value of
relative line-intensity, which is shown ... by most reduction curves
... corresponds to the decrease in , as for the same
and smaller
smaller surface brightness means smaller luminosity.
If we take account, however, of the direct influence of temperature on
ionization, which acts much more strongly in the opposite direction,
we must expect equal ionization in the more advanced types for much
smaller g and higher luminosities, contrary to the empirical reduction
curves. It looks as if this effect is compensated by some other direct
influence of temperature on the spectrum.”[419]
The influence suspected by Pannekoek may be found, at least in
part, in the “theoretical decrease with increasing temperature and
density in the quantity of material overlying the photosphere. Thus
the contrast between line and continuous background tends to become
less along the giant series (since, furthermore, for the
same abundance of active material, a given line is formed always at
the same depth).”[420] This suggestion was advanced by Stewart to
account for the observed displacement, towards cooler classes, of the
maxima of absorption lines discussed in Chapter X. It is certain that
some such factor will be operative in the reversing layer, but it is
believed that the burden of the shift of maxima should be borne by
the effective level, which has been discussed in more detail in the
[Pg 144]
preceding chapter. It would be of interest to compare the two effects
quantitatively, but the effect of temperature gradient has not yet
formed the basis of numerical predictions.
PREDICTED EFFECTS ON INDIVIDUAL LINES
The discussion involving the average ionization potential appears to permit of more rigorous treatment. Suppose the “average ionization potential” of Stewart’s discussion to be replaced by the ionization potential corresponding to the atoms whose lines are at maximum for the class in question. It then follows directly from theory that the effects of lowered pressure on the different classes of lines will be as below:
| Atom | Line | Effect of lowered pressure | |
|---|---|---|---|
| Hotter than class | Cooler than class | ||
| for maximum | for maximum | ||
| Neutral | Ultimate | Weakened | .... |
| Neutral | Subordinate | Weakened | Weakened |
| Ionized | Ultimate | Weakened | Strengthened |
| Ionized | Subordinate | Weakened | Strengthened |
It is especially to be noted that all lines should theoretically be weakened in passing from dwarf to giant, excepting the lines of an ionized atom at temperatures lower than those required to bring them to maximum. This leaves out of account the effect of photospheric depth, which will be introduced later as a correcting factor.
The case of the ultimate lines of the ionized atoms is of especial interest. At their maximum, if the Fowler-Milne theory is correct, ionization is almost complete, and more than 99 per cent of the element is giving the ionized ultimate lines. At a temperature higher than that required for maximum, lowered pressure can “increase” the ionization only by the removal of the second electron. By this process the intensity of the ionized ultimate lines is decreased, since the number of singly ionized atoms is thereby reduced. The fall from maximum towards the hotter stars, which is displayed by the ionized lines of Ca+, Sr+, and Ba+ can be due only to the progress of second ionization, and there seems to be no escape from the conclusion that [Pg 145] the ultimate lines of the ionized atom should theoretically decrease in strength, with lowered pressure, for stars hotter than those required to bring the lines to maximum. The point is made increasingly clear when it is recalled that, at the maximum, all of the substance is presumably at work giving the lines in question. It is not therefore possible to increase the number of active atoms by any process whatever that involves merely a change in pressure.
For ionized subordinate lines the theoretical effect should be the same as for the ultimate lines, for the fall after maximum is here again caused by the increase in the number of doubly ionized atoms, and the consequent decrease in the number of those singly ionized. Thus, although the subordinate lines are not already using all the available atoms at maximum, so that increased intensity with lowered pressure is possible, it would still appear that they should be weakened at temperatures higher than that corresponding to maximum intensity in the spectral sequence.
The pure pressure effects just discussed will be superposed upon the Stewart effect, which depends upon the photospheric depth. The latter will cause a general increase in the strength of all lines from dwarf to giant, as a result of the greater amount of matter lying above the photosphere in the giant. The two effects are observed together when direct intensity measures are employed, such as the estimates embodied in Chapter VIII, while the pressure effect is given almost purely when differential estimates of intensity for the same spectrum are used, as in most investigations of spectroscopic parallax. The observational evidence from both sources will now be put forward, in order to examine the sufficiency of the theories that have been advanced to account for the absolute magnitude effects.
The empirical relations used in the estimation of spectroscopic parallax should provide material for examining the simple pressure effect, as they are derived from the ratio of two lines in the same spectrum. Unfortunately the line ratios actually in use were selected [Pg 146] because they were convenient to measure, and gave (empirically) consistent results, not for reasons of theoretical tractability. Fourteen line ratios are used, for example, by Harper and Young,[421] but only four of these consist of pairs of unblended lines with known series relations. It is only for such lines that a useful test of theory can be made.
| M | = | +7 | +8.8 | +9.2 | +11.0 | +13.2 | ||||
| +6 | +13.3 | |||||||||
| +5 | +3.5 | +5.0 | +7.4 | +9.6 | ||||||
| +4 | +10.0 | +10.8 | ||||||||
| +3 | -1.8 | +0.5 | +3.8 | +6.7 | ||||||
| +2 | +6.7 | +7.0 | +7.6 | +10.0 | ||||||
| +1 | -7.2 | -3.8 | +0.2 | +3.2 | ||||||
| 0 | +3.5 | +3.4 | +3.2 | +3.0 | ||||||
| 1 | -12.9 | -8.2 | -3.2 | -0.3 | ||||||
| -2 | +0.3 | -0.2 | -1.4 | -3.7 | ||||||
| -3 | -12.1 | -7.3 | -3.8 | |||||||
| -4 | -2.8 | -4.2 | -5.8 | -10.0 |
| M | = | +6 | -2.0 | -1.4 | ||||||
| +5 | -1.5 | -0.5 | 0.0 | +1.0 | ||||||
| +4 | +1.2 | +1.3 | ||||||||
| +3 | +1.8 | +3.3 | +4.4 | +4.5 | ||||||
| +2 | +5.0 | +3.0 | ||||||||
| +1 | +4.8 | +6.5 | +7.8 | +7.6 | ||||||
| 0 | +6.5 | +4.7 | ||||||||
| -1 | +8.6 | +9.3 | +11.0 | +11.0 | ||||||
| -2 | +12.0 | +8.6 | +8.6 | +8.2 |
| M | = | +6 | -18.1 | |||||||
| +5 | -3.7 | -5.8 | -9.6 | -14.7 | ||||||
| +4 | -15.3 | |||||||||
| +3 | -1.0 | -3.3 | -6.6 | -11.0 | ||||||
| +2 | -12.4 | |||||||||
| +1 | +1.7 | -0.6 | -3.7 | -7.5 | ||||||
| 0 | -9.4 | |||||||||
| -1 | +4.5 | +2.0 | -0.9 | -4.0 | ||||||
| -2 | -6.6 | |||||||||
| -3 | +7.2 | +4.7 | +2.0 | -0.2 |
| M | = | +6 | +7.4 | +6.2 | ||||||
| +5 | +6.2 | |||||||||
| +4 | +4.3 | +3.0 | ||||||||
| +3 | +3.0 | |||||||||
| +2 | +1.3 | 0.0 | ||||||||
| +1 | 0.0 | |||||||||
| 0 | 0.0 | -2.0 | ||||||||
| 1 | +2.6 | |||||||||
| -2 | +2.0 | +0.7 | ||||||||
| -3 | +5.2 |
[Pg 147]
The preceding table contains a transcription of the reduction-curve material given by Harper and Young for the four pairs of lines mentioned. Tabulated quantities are the “step differences” for the classes at the heads of the columns, and the absolute magnitudes contained in the first column.
Presumably the irregularities of the observed curves have been smoothed out in forming the reduction table, but the figures will certainly give an indication of the direction in which a given line is affected by absolute magnitude.
The predicted effect of lowered pressure upon the lines involved is contained in the table that follows:
| Line | Source | Max. | Effect of lowered pressure |
|---|---|---|---|
| 4071 | Fe (sub) | weakened throughout | |
| 4077 | Sr+ (ult) | strengthened in |
|
| 4215 | Sr+ (ult) | strengthened in |
|
| 4247 | Sc+ (?) | strengthened throughout range | |
| 4250 | Fe (sub) | weakened throughout | |
| 4455 | Ca (sub) | weakened throughout | |
| 4494 | Fe (sub) | weakened throughout |
The predicted changes in the line ratios with lowered pressure are
therefore as follows:
The ratio behaves in exact accordance with
prediction, and
which decreases and then
increases again, offers no evidence for or against the theory. The
two remaining ratios, involving the two Sr+ lines, display a lack of
agreement with theory for the
and
classes, apparently
owing to the strengthening of the Sr+ lines with high luminosity,
even at temperatures higher than those at which they attain maximum
[Pg 148]
intensity. The strengthening of Sr+ with high luminosity is one of
the best-attested facts of observational astrophysics, and it is a
serious deficiency in theory if the observed behavior of the lines in
the hotter stars cannot be explained. The question will be further
discussed presently.
The material obtained by the writer, and summarized in a preceding chapter,[422] may be used in making a test of the predicted pressure effects by means of direct estimates. As was pointed out above, the lines of a giant are stronger than those of a dwarf, owing to the greater photospheric depth in the former. The practical difficulty of making comparable estimates upon sharp and somewhat hazy lines must also be considered in the discussion of the results. Clearly some numerical correction is required, in order to allow for the Stewart effect, and this has been done in a somewhat arbitrary manner in forming Table XXIV. It is assumed that the mean increase in intensity for such lines as are strengthened will be equal to the mean decrease in intensity for such lines as are weakened. For each spectral class this assumption provides a correcting factor, which never exceeds one scale unit.
The table that follows contains the material derived from the measures
enumerated in Chapter VIII, and from other sources, bearing on the
intensity differences between giants and dwarfs of the same spectral
class. All the available estimates have been used. Successive columns
give the line, the atom, the predicted behavior, and the observed
difference in the sense giant-dwarf, for the Classes ,
,
,
,
, and
. The symbols
,
, and
, following the atom, denote ultimate, neutral, and enhanced
lines, respectively. The number of stars contributing to each entry
will be seen from the list on p. 119, Chapter VIII. The notation is as
follows: 0 = no change; ± 0 = between 0 and 1; ± 1 = between 1 and 2; ±
2 = between 2 and 3; and so on. The values for
are taken from
Menzel’s measures[423] of
Indi and
Tauri, “the
scale of intensities being (0) no difference, (1) a little stronger
[Pg 149]
(2) much stronger, (3) very much stronger.” The signs from Menzel’s
table are reversed, in accordance with the notation used in the
present table. In the column headed
are the signs indicating
the direction in which the corresponding lines are affected in that
class,[424] for which quantitative measures have not been published.
The letters “
” and “
” in the column headed
refer to
strengthening or weakening of lines, as observed by Baxandall[425] in
a comparison of the solar spectrum with that of Capella. Baxandall’s
estimates are inserted to supplement the present material. The numerous
gaps in the table result from the difficulty of seeing the fainter
lines in the dwarf spectrum.
| Line | Element | Predicted Effect | Observed Effect | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | 0 | + | ||||||||||
| 3933 | Ca+ | * | +1 | .. | .. | .. | .. | 0? | + | |||
| 3944 | Al | u | .. | .. | +0 | + | -2 | .. | .. | .. | - | |
| 3953 | Fe | n | ( |
.. | +0 | + | -2 | .. | .. | .. | .. | |
| 3961 | Al | u | .. | .. | +0 | + | -2 | .. | .. | .. | - | |
| 3968 | Ca+ | * | +1 | .. | -1 | .. | .. | 0? | + | |||
| 3999 | Ti | u | .. | .. | +0 | .. | -1 | .. | .. | .. | .. | |
| 4005 | Fe | n | .. | .. | +0 | .. | 0 | .. | .. | .. | .. | |
| 4031 | Mn | u | .. | .. | -2 | -1 | -1 | .. | .. | 0 | .. | |
| 4041 | Mn | n | .. | .. | -1 | -1 | -2 | .. | .. | -0 | .. | |
| 4046 | Fe | n | .. | .. | -1 | -1 | 0 | -1 | -1 | -2 | .. | |
| 4064 | Fe | n | .. | .. | -1 | -2 | .. | +2 | 0 | -2 | .. | |
| 4068 | FeMn | n | .. | .. | -1 | .. | .. | +1 | -1 | .. | .. | |
| 4072 | Fe,- | n | .. | .. | 0 | +4 | .. | .. | -1 | -2 | .. | |
| 4077 | Sr+ | * | 0 | 0 | +1 | s | 0 | +3 | + | |||
| 4084 | Fe | n | .. | .. | -1 | +1 | 0 | 0 | .. | .. | .. | |
| 4101 | H | n | .. | .. | -1 | -1 | +1 | -4 | 0 | -1 | + | |
| 4132 | Fe | n | .. | .. | 0 | +2 | +1 | .. | +0 | -1 | .. | |
| 4135 | Fe | n | .. | .. | -1 | .. | 0 | .. | +0 | .. | .. | |
| 4144 | Fe | n | .. | .. | -1 | 0 | +2 | 0 | +0 | -1 | .. | |
| 4167 | ? | -1 | .. | -1 | -1w | 0 | .. | .. [Pg 150] | ||||
| 4172 | Fe+ | * | +1 | +1 | +3 | +1 | +0 | .. | .. | |||
| 4177 | Fe+ | * | +1 | .. | +2 | .. | .. | .. | .. | |||
| 4215 | Sr+ | * | 0 | 0 | +2 | +3 | +0 | +1 | + | |||
| 4227 | Ca | u | .. | .. | -1 | -1 | 0 | -2 | -0 | -2 | - | |
| 4247 | Sc+ | * | .. | 0 | .. | +1 | .. | +1 | .. | .. | ||
| 4250 | Fe | n | .. | .. | 0 | -2 | -1 | -2 | -1 | -2 | .. | |
| 4254 | Cr | u | .. | .. | -1 | .. | -1 | -1 | -1 | -1 | .. | |
| 4260 | Fe | n | .. | .. | -1 | -2 | -1 | -2 | .. | -1 | - | |
| 4272 | Fe | n | .. | .. | -1 | -2 | .. | 0 | +0 | -1 | .. | |
| 4275 | Br | u | .. | .. | -1 | .. | .. | 0 | +0 | -1 | .. | |
| 4290 | Cr | u | .. | .. | 0 | -2 | 0 | .. | +0 | -1 | .. | |
| 4298 | Ti, Ca | .. | .. | -1 | -2 | 0 | .. | 0 | .. | .. | ||
| 4308 | Fe | n | .. | .. | 0 | +1 | 0 | .. | .. | -1 | .. | |
| 4315 | Fe+ | * | .. | 0 | +1 | +2 | .. | .. | .. | .. | ||
| 4321 | Sc+ | * | .. | +1 | .. | .. | s | .. | .. | .. | ||
| 4326 | Fe | n | .. | .. | 0 | +1 | +1 | -2w | 0 | -2 | .. | |
| 4340 | H | n | .. | .. | -2 | -7 | -1 | -4 | -0 | -1 | + | |
| 4352 | CrMg | .. | .. | 0 | +2 | 0 | +1 | +0 | -3 | .. | ||
| 4360 | Cr | n | .. | .. | 0 | .. | +1 | .. | .. | .. | .. | |
| 4370 | Fe | n | .. | .. | +1 | .. | 0 | .. | +0 | .. | .. | |
| 4376 | Y+ | * | .. | -1 | +2 | 0 | .. | +1 | +2 | .. | ||
| 4383 | Fe | n | .. | .. | 0 | +3 | +1 | -2 | -4 | -2 | .. | |
| 4405 | Fe | n | .. | .. | -1 | .. | .. | 0 | -1 | -2 | .. | |
| 4415 | Fe+ | * | .. | +1 | 0 | +3 | 0 | 0 | -1 | .. | ||
| 4435 | Ca | n | .. | .. | -1 | .. | +1 | .. | 0 | -2 | - | |
| 4444 | Ti+ | * | .. | 0 | 0 | +1 | s | -3 | .. | .. | ||
| 4455 | Ca | n | .. | .. | -2 | .. | -1 | w | -1 | -3 | - | |
| 4476 | Fe | n | .. | .. | -1 | .. | +1 | -1 | .. | .. | .. | |
| 4481 | Mg+ | * | .. | .. | -1 | 0 | 0 | 0 | +0 | +1 | .. | |
| 4490 | Fe | n | .. | .. | 0 | .. | .. | +1 | -0 | +2 | .. | |
It is seen from the table that the general agreement with the anticipations of theory is satisfactory, and that the deviations, when they occur, rarely exceed one unit. The agreement is not less good than would be expected of the material, since the measures are here used differentially. The majority of the discrepancies are apparently accidental; for example, the deviations shown by the first six entries in the first column are almost certainly the result of better definition in the giant spectrum. There remains, however, the same [Pg 151] discrepancy for the lines of Sr+ that was noted in the earlier part of the chapter. There can be no doubt that these lines are stronger in giants than in dwarfs.
The strengthening of the ionized lines of the alkaline earths is
explained, when the spectra are examined, by the fact that the neutral
lines are still fairly strong long after the ionized lines have passed
their maximum—neutral strontium[426] is found at and neutral
calcium[427] at
. The lowered pressure, then, must increase
the concentration of singly ionized atoms at the expense of the
residual neutral atoms. There is, however, apparently no satisfactory
theoretical explanation of the survival of large quantities of neutral
calcium long after the ionized atoms have passed their maximum. The
effects predicted above would appear to be the only ones that can be
anticipated if the theory holds rigidly. Clearly some factor such as
effective level must be further considered.
THE STRONTIUM LINES
The strontium problem is perhaps one that will lead to more
comprehensible results when it is treated as a whole. It is impossible
to resist the feeling that there is some definite abnormality
associated with strontium. The “strontium stars” in the still earlier
classes, where the lines 4215, 4077 appear with great intensity,
and the stars
Circini and
Equulei, as
well as the apparently erroneous absolute magnitudes obtained by
the spectroscopic method for several other stars of low intrinsic
luminosity, all point in some such direction.
It may be that these phenomena are a result of an abnormal abundance or
distribution of the element. It is not, therefore, entirely necessary
to assume that the theory is here at fault, although until the behavior
of strontium has been satisfactorily interpreted, that possibility
cannot be rejected. It is significant that calcium and barium show
similar absolute magnitude behavior. In any case, the ionized strontium
lines cannot be cited, as has sometimes been done, in demonstrating
[Pg 152]
that the absolute magnitude effect is due to pressure. What is actually
shown is that the concentration of singly ionized atoms is more greatly
increased at the expense of the neutral atoms than it is reduced by the
formation of doubly ionized atoms. Since a pressure effect operates
by the discouragement of recombination, it would be inferred that the
recombination of singly ionized atoms with electrons to form neutral
atoms is less readily encouraged than the recombination of doubly
ionized atoms with electrons to form singly ionized atoms. Evidently
the problem is a complex one. If the maximum of the strontium lines
were at (where theory first predicted it, and where the earlier
measures actually placed it) there would be no anomaly to explain;
but two independent observers[428] place it definitely at
or
, and there can be little doubt that this is actually the
correct position of the maximum.
The result of the study of absolute magnitude effects is disappointing. It appears that the observed phenomena are qualitatively explained in a satisfactory manner, as due to lowered pressure, or, more accurately, to low surface gravity. There is, however, a serious discrepancy in the case of the lines whose variation with absolute magnitude is perhaps best established, and upon which the most important results have been based. The results, being empirical, are of course unimpaired, and it would seem that the theory requires to be amended. Furthermore, it does not yet appear to be possible to use the observed changes of intensity for the direct estimation of pressure differences, because of the large number of variables involved and particularly because of the superposition of the pure pressure effect upon the effect of photospheric depth.
[412] Adams and Kohlschütter, Mt. W. Contr. 89, 1914.
[413] B. A. N. 19, 1922.
[414] Milne, Phil. Mag., 47, 209, 1924.
[415] Pannekoek, B. A. N. 19, 1922.
[416] Pop. Ast., 31, 88, 1923.
[417] Pop. Ast., in press.
[418] B. A. N. 19, 1922.
[419]
In Pannekoek’s notation, a is surface brightness,
is radius, and
, surface gravity.
[420] Stewart, Pop. Ast., in press.
[421] Pub. Dom. Ap. Obs., 3, 1, 1924.
[423] H. C. 258, 1924.
[424] Adams, Pub. A. S. P., 28, 278, 1916; Adams and Joy, Pub. A. S. P., 36, 142, 1924.
[425] Pub. Solar Phys. Com., 1910.
[Pg 153]
[Pg 155]
IN the opening chapter the statement was made that “the astrophysicist is obliged to assume [the validity of physical laws] in applying them to stellar conditions.” The astrophysical evaluation of physical constants might therefore seem, from our avowed premises, to involve a circular argument. In certain special cases, however, the process appears to be legitimate, and the results of three investigations are contained in the present chapter. The first of these investigations involves the derivation of spectroscopic constants, assuming the series formula; the second consists of an extrapolation of the results of Chapter X to the estimation of unknown ionization potentials; and the third constitutes a discussion made possible by the knowledge of the stellar atmosphere that has been attained with the aid of ionization theory.
THE RYDBERG CONSTANT FOR HELIUM
The wave-lengths of a series of lines can be measured in the spectrum of a star, and the series identified with a series observed in the laboratory. The occurrence in stellar spectra of series that can be identified with the series given by terrestrial atoms presumably shows that similar relations govern the atomic processes in the two sources. That series formulae of the same type are applicable to the stellar and terrestrial atom is indeed rather an observational fact than an assumption. By inserting into the appropriate series formula the observed stellar frequencies, a physical constant involved may be evaluated, and the extent of the agreement with the corresponding value from the laboratory may be determined.
[Pg 156]
H. H. Plaskett[429] has measured the wave-lengths of the lines of the
Pickering series () of He+ in the spectra of three
stars, incidentally separating the alternate Pickering lines from
the Balmer lines for the first time. The formula that connects the
frequencies of the lines with the constants associated with the atom is
Plaskett discussed the theory, and derived from the measured
wave-lengths of five lines the mean value of 109722.3 ± 0.44 for the
constant . The value determined in the laboratory by Paschen
is 109722.14 ± 0.04. Plaskett’s comment on the agreement is as
follows: “It was not to be expected that there would be any startling
changes.... It is of interest, however, to note that these “stellar”
determinations are in agreement with the terrestrial values, in
so far as it shows that the implicit assumption of identical atomic
structure, identical electrons, and identical laws of radiation on the
earth and in the stars, is in some measure justified.”
CRITICAL POTENTIALS
The theory outlined in the preceding chapters was used in determining the astrophysical behavior of lines corresponding to known series relations. When the validity of the theory has been established, it is possible, as was pointed out by the writer,[430] by Fowler and Milne,[431] and by Menzel,[432] to deduce the ionization potentials of lines of unknown series relations from their astrophysical behavior. The ionization potentials were estimated in this way for the table in Chapter I.
In general the observations show that the higher the ionization
[Pg 157]
potential, the higher the temperature at which the corresponding lines
attain maximum. This is in strict accordance with theory. It is not
possible to predict the exact form of the relation between temperature
of maximum and ionization potential. For the observed cases in which
(the ultimate lines),
. It
would appear that
should approach zero as
approaches zero. But in this case
(the
negative energy of the excited state, which must always be less
than
) also approaches zero, and the relation becomes
indeterminate. The form of the curve as
approaches zero has merely a
theoretical interest, as no known element has an ionization potential
of less than four volts. In the present application the relation will
be treated as an empirical one. The curves given by the writer and by
Menzel for the relation between ionization potential and
display a good general regularity, and the deviations, as was pointed
out in a previous chapter,[433] probably arise from differences of
effective level. Owing to this source of irregularity, great accuracy
is not to be anticipated in the deduced ionization potentials.
The effective level is at the greatest height for lines of low
excitation potential. The excitation potentials corresponding to the
astrophysically important lines of the once, twice, and thrice ionized
atoms in the hotter stars are in all known cases highland thus the
error introduced by neglecting to correct for effective level is small.
The error introduced by an excitation potential of the wrong order
is, moreover, a constant and not a percentage error, and thus becomes
less serious in estimating high ionization potentials. Accordingly the
deduced ionization potentials will probably be of the right order.
The relation connecting ionization potential and may, for
our purposes, be treated as an empirical relation between ionization
potential and spectral class. This mode of regarding the question has
the advantage of being quite independent of the adopted temperature
scale. We merely assume that the sequence of spectral classes is a
temperature sequence. The ionization potentials corresponding to lines
[Pg 158]
of known maximum may then be deduced by interpolation.
| Element | Ionization Potential | Authority |
|---|---|---|
| C++ | 45 | Payne |
| N+ | 24 | Ibid. |
| N++ | 45? | Ibid. |
| O+ | 32 | Ibid. |
| O++ | 45 | Fowler and Milne |
| Si | 8.5 | Menzel, Payne |
| S+ | 20 | Payne |
| S++ | 32 | Ibid. |
| Sc+ | 12.5 | Menzel |
| Ti+ | 12.5 | Ibid. |
| Fe | 7.5 | Ibid. |
| Fe+ | 13 | Ibid. |
The value of is dependent on the effective level, and hence
upon the excitation potential. Without the introduction of unjustified
assumptions, more than one critical potential cannot be deduced
from observations of intensity maximum. The excitation potential
corresponding to a line could be roughly inferred from the observed
maximum, by observing the shift of predicted maximum produced by the
level effect (discussed in Chapter IX) if the ionization potential were
known. There are, however, no data as yet that could be used in drawing
inferences of this kind.
DURATION OF ATOMIC STATES
The successful application of theory to the astrophysical determination of the life of an atom requires the fulfilment of special conditions. The requirements of the idea developed by Milne[434] demand that the atom shall exist in appreciable quantities in only two states simultaneously. This condition is fulfilled by the ionized atoms of the alkaline earth elements, and it is with calcium that the estimates here discussed are concerned.
[Pg 159]
The investigation relates to the calcium present in the high-level
chromosphere, where, owing to remoteness from the photosphere, thermal
ionization is negligible. Photoelectric ionization may be operative in
removing the first electron from the calcium atom, but the sun is too
deficient in light of wave-length 1040 for second stage photoelectric
ionization to be appreciable. The calcium present in the high-level
chromosphere is probably largely in the once ionized condition, since
an atom once ionized is likely to remain so for a long time, owing to
the scarcity of free electrons in the tenuous outer regions of the sun.
The present investigation neglects altogether the neutral and doubly
ionized calcium atoms, and furthermore assumes that the transfers
corresponding to the and
lines of the
series are the only ones that occur in appreciable quantities. The
latter assumption is apparently not accurately fulfilled, as the
lines of Ca+ have recently been detected in the high
level chromosphere.[435]
[Pg 160]
In the simple case of the Ca+ atom (neglecting the small number of
atoms that are giving rise to the lines) only two states
of the atom are possible: the normal state, called by Milne the
state, and the excited, or
state. A given atom
exists alternately in these two states. If
be the average time
spent in the
state, and
the average time spent in
the
state, the average time spent by an atom in traversing
its possible cycle of changes is
. Now
is
connected with the probability of an emission, and
with the
probability of an absorption. Clearly
depends at least partly
upon the energy supply, but
is an atomic constant measuring
the readiness with which the atom recovers its normal state after an
absorption. It is, in fact, the “average life” evaluated from Milne’s
equations. The ratio
, expressing the relative
tendencies of Ca+ atoms to emit and to absorb the
and
lines, is the residual intensity at their centers, with respect to the
adjacent continuous background.
Einstein’s theory of radiation[436] is used in evaluating
from the relation
where
is the ratio
.
From ordinary quantum principles,
and both
and
may be derived by eliminating between
the two equations.
The only measured quantity in the formula is , and from the fact
that
is the “residual intensity” within an absorption line,
we know that it must lie between 0 and 1. Hence a maximum value of
may be derived
for
. On the insertion of the data given by Schwarzschild[437]
for the residual intensity of the
and
lines, 2.6
magnitudes fainter than the continuous background, and corresponding
to a value of
equal to 0.11, the deduced value of
is
. The agreement
of this value with those obtained in the laboratory for the atoms of
hydrogen and mercury has been commented upon in a previous chapter.[438]
[429] H. H. Plaskett, Pub. Dom. Ap. Obs., 2, 325, 1922.
[430] M. N. R. A. S., 84, 499, 1924.
[431] H. C. 256, 1924.
[432] H. C. 258, 1924.
[434] Milne, M. N. R. A. S., 84, 354, 1924.
[435] Curtis and Burns, unpub.
[436] Phys. Zeit., 18, 121, 1914.
[437] Sitz. d. Preuss. Ac., 47, 1198, 1914.
[Pg 161]
THE greater part of the present work has dealt with the discussion and
interpretation of the normal spectral sequence, to
, and
the main features of the series have been satisfactorily attributed
to thermal ionization at high temperatures. Such a discussion must
naturally be the first step in the analysis of the stellar atmosphere.
When the more general results of observation have been reduced, in
some measure, to an orderly system, it becomes possible to consider
special problems involving stars or groups of stars, which lie outside
the system, or which, though included in the system, display definite
abnormalities.
The special problems of stellar spectroscopy are very numerous. We may
mention the novae, the Class stars,
stars that show emission
lines, the problem of
-star classification and the peculiar
stars,
stars that display both giant and dwarf spectral
characteristics, the classification of the
stars, the apparent
splitting into three groups of the spectral sequence for temperatures
below 4000°, the problem of the c-stars, the Cepheid variables with
their variable spectra, and the variables of long period.
It is not possible, in a work like the present, to touch upon many of
these subjects, and the writer has selected for brief discussion three
upon which she can contribute new material: the problem of the
stars, the classification of the
stars, and the interpretation of
the spectra of the stars that display the c-characteristic.
THE STARS OF CLASS
The statistically negligible class containing the stars is
placed, at the present stage of investigation, at the top of the
stellar sequence. These spectra indicate higher excitation than
[Pg 162]
those of any other class, and ionization theory distributes their
temperatures between 25,000° and 40,000°. Their spectra are among the
most puzzling encountered in the whole stellar sequence, and theory has
hitherto been unsuccessful in suggesting the conditions that produce
them.
A hundred and forty non-Magellanic stars[439] are enumerated in
the Draper catalogue, and in addition a small number of apparently
faint
stars should probably be transferred to Class
, as
Victoria has already done[440] for a group of stars in Monoceros. The
stars have a very definite distribution; they lie either very
near the galactic plane, or in one of the Magellanic clouds, or they
constitute the nuclei of planetary nebulae.
The stars other than the nuclei of planetaries have high
intrinsic luminosities, but the material is insufficient for a
satisfactory estimate of the absolute magnitudes of the non-Magellanic
stars; various indications point to a value at least as high as
-4. For the Magellanic
stars, absolute magnitudes as great as
-6.7 have been derived.[441] The measured parallaxes of the planetary
nebulae, however, give for the nuclei absolute magnitudes[442] in the
neighborhood of +8. The wide difference in absolute magnitude can
merely be pointed out; it has never received adequate explanation.
The masses are presumably very high for the stars, though but few
have been accurately measured. The star B.D. 6°1309, a spectroscopic
binary reported by J. S. Plaskett,[443] has a minimum mass eighty times
that of the sun, and the stars 29 Canis Majoris and
Orionis
also appear to be very massive.[444]
The spectra of the stars of Class differ widely among themselves,
but they are signalized by the lines of ionized helium, which are
normally observed only in this class and in the nebulae. In addition,
the atoms of H, He, Mg+, C++, 0++, N++, and Si+++ are represented.
[Pg 163]
The atmospheres of these stars are thus in a state of high ionization,
which is attributed to high temperature, in harmony with the work
already outlined in previous chapters. The spectra of the stars
of Class
have been described by W. W. Campbell,[445] Miss
Cannon,[446] Wright,[447]
H. H. Plaskett,[448] J. S. Plaskett,[449] and
the writer,[450] and the material upon which the present discussion is
based will be found in the papers quoted.
Many of the stars, such as
Canis Majoris, H.D. 150135,
H.D. 159176, H.D. 199579, H.D. 164794, H.D. 167771, H.D. 165052, give a
pure absorption spectrum, containing the Balmer series of hydrogen, the
lines of Si+++, the Pickering and “4686” lines of He+, and the N++ line
at 4097. The stars are mentioned in order of increasing ionization,
with He+ rising in intensity. The other lines mentioned are clearly
beyond their maximum, and fall progressively in strength. The stars
mentioned probably represent successive steps in a sequence with rising
temperature, connecting directly with Class
, and ranging from
25,000° to 35,000°.
This sequence of stars would form a simple and explicable series
if it were an isolated group. There are, however, other stars, with
spectra so similar to those of the series just quoted that there can
be no doubt of a close relationship—they display absorption lines due
to the same elements with about the same relative intensities—but
emission lines tend to occur in various parts of the spectrum. 29 Canis
Majoris,
Muscae, and
Puppis have absorption spectra
which resemble those in the sequence just quoted, but at 4650 and 4686
there are emission lines or “bands.” The bright lines are so wide and
diffuse, in
Muscae, as to be blended together at their
edges, while they are sharp and clear in the other two stars. Between
the two series just quoted—pure absorption stars and absorption stars
[Pg 164]
with some bright lines, comes
Circini, a star which has all
the characteristics of the first group, and also shows faint emission
on the red edge of the absorption lines at 4650 and 4686.
There are other stars, such as Cephei,
Persei, S
Monocerotis, H.D. 152408, H.D. 112244, and
Orionis, that have
absorption spectra such as were described for the first group, but
which display faint emission lines at the red edge of the hydrogen and
helium lines. It is obvious that all the stars so far enumerated may
legitimately be classed together, but that there is a very universal
tendency for emission lines and bands to appear in them. This tendency
is so marked in the stars that are still to be mentioned as to
constitute their most salient feature.
In the subgroup of the stars which are collectively designated
the Wolf-Rayet stars, the emission lines are the most conspicuous
characteristic of the spectrum. The best known and brightest star
of this group is
Velorum, which possesses an extremely
complex spectrum, made up of an absorption spectrum similar to that
of
Circini, and a large number of wide “emission bands.” An
analysis of the spectrum of
Velorum has been published by
the writer;[451] all the stronger lines of H, He, He+, C+H-, O++, N++,
Si+++, and Mg+ are represented in the spectrum, and a comparatively
small number of lines remains unidentified.
Other stars that have spectra in which the emission lines are
the prominent feature are H.D. 151932, H.D. 92740, H.D. 93131, H.D.
152270, H.D. 156385, and H.D. 97152. All of these stars, excepting the
last, have also absorption spectra displaying the lines of H and He+.
The lines of N++ and Si+++ are absent, and these stars are therefore
probably at the extreme high-temperature end of the sequence.
The question of absorption in the Wolf-Rayet spectrum is a difficult
one, because the bright lines show up before any other feature of the
spectrum, while an appreciable continuous background is necessary
before absorption can be detected. The detection of absorption lines
[Pg 165]
in many stars, such as H.D. 152270, where no absorption had previously
been recorded, has resulted from a general survey of spectra that had
received exposures sufficient to bring out the continuous background.
The writer has been led to the opinion that absorption is a common,
if not universal, feature of all the Wolf-Rayet stars, except those
classed at Harvard as . This subclass has bright bands that
do not coincide with those of the other
stars, and among them
absorption lines appear to be exceptional.
It is perhaps to be expected that absorption should normally occur among the Wolf-Rayet stars, as it does among the other classes. In all other stars, the bright lines that appear are the abnormal feature, and are superposed on a normal continuous spectrum crossed by absorption lines. Spectra consisting of bright lines only do not occur elsewhere, excepting for the gaseous nebulae. The gaseous nebulae have, presumably, no photosphere, and the continuous background that they sometimes display is probably the result of reflected and transformed starlight; absorption lines appear normally to accompany the existence of a photosphere.
It is clear that the stars are a very complex group. Those that
have pure absorption spectra can be arranged in a series immediately
preceding
; and those that show a similar absorption spectrum,
with faint superposed emission, presumably also fit into the sequence.
When a
star shows emission lines (as
Cassiopeiae does)
it is placed in the
class appropriate to its absorption spectrum,
with the additional designation “e” to indicate the abnormality, and
the same procedure appears to be equally satisfactory for the
stars.
As emission predominates more and more, the spectrum resembles those of the normal members of the sequence less and less. If a star has an absorption spectrum it can always be assigned a place in the sequence, and this method of arrangement appears to be logical. But it is clear that the sequence so formed is no longer physically homogeneous. The stars that have no absorption lines, although some of them have obvious affinities with stars that have absorption spectra, have [Pg 166] moreover no place in a sequence formed on the basis of absorption intensities.
It is, of course, possible to devise a self-consistent scheme for the
arrangement of a limited number of the stars, and such a scheme
is, for many purposes, both desirable and convenient. It is, however,
exceedingly hard to know where the division should be drawn between
“absorption” and “emission” stars. Perhaps the most satisfactory plan
is to treat all
stars as a sequence, with special comment
for the large number of them that require it.
THE CLASS STARS
(a) The Balmer Lines.—The spectra of the stars are
dominated by the Balmer series of hydrogen, which, with the exception
of the
and
lines in the cooler stars, are stronger at
than any other line seen in the stellar sequence. The maximum
of the Balmer series has been stated[452] to occur at
, and
this value was used by Fowler and Milne[453] in calibrating their
temperature scale based upon ionization theory. It is in accordance
with theory that the subordinate lines of hydrogen, with ionization
potential 13.54 volts, and excitation potential 10.15 volts, should
have their maximum at about 10,000°.
The position of the maximum can be placed elsewhere by the use of
special stars in estimating the line-intensities. The intensity of the
hydrogen lines is in fact unusually difficult to determine, as they
differ from star to star in width, wings, and probably also in central
intensity. Using a series of individual stars, Menzel[454] placed the
maximum at , with the note that “on the average the lines seem
to be strongest in Classes
to
, but the mean intensity
is often greatly exceeded in certain
,
and even
stars.” A general study of the Class
spectra confirms
the statement that the mean intensity at maximum is often exceeded
for individual stars in other classes, and the writer is inclined to
be of the opinion that no significant maximum can be derived from a
[Pg 167]
limited number of estimates. The maximum given in the Henry Draper
Catalogue is the product of the examination of an enormous number of
very short dispersion plates, and is entitled to a greater weight
than any other. In the estimation of such strong lines, the width and
especially the wings are likely to affect the estimates extensively,
and short dispersion plates probably reduce the difficulty, and permit
of the greatest possible accuracy. It must be emphasized that the
maximum given in the Henry Draper Catalogue cannot be superseded by
measures made on an arbitrary selection of stars, such as is used
when stars bright enough to be photographed with (say) two objective
prisms are discussed, for it is a generalization from the most complete
data hitherto examined, or to be examined for some time to come. The
non-homogeneity of the
classes, presently to be discussed,
includes wide variations in the widths of the hydrogen lines, and
renders unnecessary any attempt to correct the hydrogen maximum at
, which appears to be of a statistical nature.
(b) Metallic Lines and Band Absorption.—The metallic lines,
which become so conspicuous in intensity in the later classes, appear
in the types immediately succeeding , and increase progressively
in strength as cooler classes are approached. In general, all the
related lines belonging to any one element appear at the same class,
although sometimes the fainter components of metallic multiplets are
not seen until the stronger components have attained a considerable
intensity. For example the weaker lines of an element that is seen at
may not appear till
. The disparity in intensity between
the components of a multiplet is usually not so great at appearance
as at maximum. The relative strengths of unblended lines conform at
maximum with the laboratory intensities, to an extent that raises
questions as to the degree of saturation[455] of the more intense
components. It seems that none of the metallic lines, excepting those
of calcium, are greatly oversaturated, even at maximum, to judge from
the relative intensities of related lines at that point.
[Pg 168]
It is within the stars that the first signs of band absorption
appear. The
band is seen in some
stars, and a drop in the
continuous spectrum of Vega around 4160 has been ascribed[456] to the
cyanogen band headed at 4215. Similar “band” absorption can be traced
in other stars of Class
, and is even seen as early as
.
Identification of the cyanogen band headed at 3885, which always
accompanies the 4125 band, would confirm the attribution to cyanogen,
but the violet band does not seem to have been observed. The wings of H
, which are often wide and conspicuous, render it difficult to
trace anything of the nature of band absorption near 3885 for an
star.
(c) The Classification of Stars.—Several lines of
evidence have indicated that the classes into which the
stars
have been divided are not physically homogeneous, and the problem of
their classification is one of the future tasks of astrophysics. It is
hoped that the writer can in the future make a more complete discussion
of the question than is here desirable, and therefore the present
treatment is to be considered merely suggestive and tentative. The
material quoted is slight, and must be increased before conclusions can
be justified.
It has been suggested[457] that a one-dimensional arrangement will
not suffice for the classification of the stars. The spectra
have been classified, at least for the hotter
types, by the
strength of the
and
lines of Ca+. With the dispersion
used in making the Henry Draper Catalogue, these lines constitute
the conspicuous difference between one spectrum and another, and
are the obvious criterion of class. If the spectra are classed by
the strength of these lines alone, the classification is of course
quite unambiguous, and for a one-dimensional sequence of spectra it
would have been ideal. That the classes so formed are not
homogeneous[458] indicates that some second variable must be described
in a satisfactory classification, and that the strength of no one line
could have been used with any greater success than that of the
[Pg 169]
and
doublet. Further, practical difficulty in duplicating the
classifications has been caused by the fact that the
and
lines are so far into the violet that they do not appear at all on
many slit spectra, such as those used at Mount Wilson, and when other
criteria are chosen for classification, it is likely that the results
will deviate somewhat from those of the Henry Draper Catalogue.
By analogy with what is observed in other types, it has been suggested
that the range in line-sharpness that is found within a given class
among the stars is an effect of absolute magnitude, and the
sharpness of the hydrogen lines has indeed been used at Mount
Wilson[459] as a quantitative measure of luminosity. From an analysis
of the widths of hydrogen lines made by Miss Fairfield,[460] it appears
that the line sharpness may be used to distinguish
stars of the
highest luminosity from those of the lowest, but that it cannot be used
for the accurate estimation of absolute magnitude between those limits.
The special problem of classifying the stars is only in its
initial stage. That the present system is inadequate is certain, but
as yet no satisfactory alternative has been proposed. The direction in
which work should be pursued is, in this instance, probably the study
of the differences between individual spectra. As the problem appears
to hinge on the presence of abnormalities within a given class, it is
of especial importance to examine the frequency, magnitude, and nature
of these abnormalities.
(d) Silicon and Strontium Stars.—There are among the
stars two small groups of especial interest—the so-called “silicon”
and “strontium” stars. These occur chiefly in
,
,
, and are distinguished by the unusual intensity of the
lines 4128 and 4131 of ionized silicon, and the lines 4077 and 4215
of ionized strontium. Such stars are regarded in the Henry Draper
Catalogue as definitely abnormal, and are individually mentioned in
the Remarks. The strontium stars in classes later than
are
[Pg 170]
apparently ordinary high-luminosity stars, and the line-intensity is
involved in the well known absolute magnitude effect.
The absolute magnitudes of the strontium stars have been supposed, on
general grounds, to be very high, but an examination of the proper
motions indicates that this is perhaps not even generally true. The
well known star
Circini is apparently a dwarf,[461]
and
Equulei has similar spectral peculiarities and proper
motion. Examples might be multiplied, but there is not enough material
at present available for a full discussion, and from what has already
been said it is evident that the strontium stars constitute no ordinary
absolute magnitude problem, although the condition that produces strong
strontium lines in some dwarf stars may be something, like low surface
gravity, that also prevails in stars of high luminosity.
There are too few parallaxes, proper motions and radial velocities
for significant statistical treatment of the silicon stars, and still
less material for the strontium stars; but the galactic distributions
of both classes indicate that their absolute magnitudes are at least
not extremely high. There does not at present appear to be sufficient
justification for the statement that these stars are “distinctly
brighter than the average.”[462] Their brightness would rather seem to
be about the same as that of a normal star.[463]
The silicon and strontium stars raise spectroscopic difficulties that
differ somewhat in the two cases. Most of the silicon stars occur at or
near , where the Si+ lines are normally at maximum intensity.
On the other hand, Sr+ has its maximum at Class
or
,
but the intensity in such
stars as
Ophiuchi and
Microscopii is as great as it is in these types. The
strontium problem illustrates the general conceptions underlying the
methods of estimating line-intensities, and will therefore be discussed
in slightly more detail.
[Pg 171]
Abnormal intensity of a spectrum line can be attributed to (1) blending, (2) unusual conditions, or (3) abnormal abundance. These conditions will be discussed in order.
(1) Blending.—Blending, excepting where lines are
spectroscopically resolved, can only be detected indirectly, by
examining the behavior of other lines belonging to the same spectral
series as the line in question. If the relative intensities of all the
lines in the series are the same as those found in the laboratory, and
if changes of intensity from class to class affect all the lines of
a series equally, it may be inferred that blending is not a serious
disturbing factor and that the abnormal intensity is due to other
causes. The close correlation between the stellar intensities of 4215
and 4077, the components of the principal doublet of ionized strontium,
in the different spectral classes, leaves little doubt that these lines
are effectively unblended in the stars, although the difference of
spectral class for the maximum of the two lines (
,
) and
the presence of a solar iron line at 4215, suggest a blend for the
latter in stars cooler than about
. It is also to be remarked
that the head of a “cyanogen” band falls at 4216.
(2) Abnormal Conditions.—Abnormal conditions permit of no
direct observational test, but it would be anticipated that they would
also affect other lines to a degree greater than is observed. The
change of temperature that would be required to raise the Sr+ lines
to their maximum strength at (10,000°) would be a fall of
about 5000°, which is quite inadmissible, for the resulting change of
spectrum would produce a
star. The required change of pressure
is also too great to be possible: this subject cannot profitably
be discussed here, and reference should be made toChapter X. The
existence of a strontium cloud has been suggested[464] by analogy with
the “calcium cloud,” and might possibly provide an explanation, as
it would furnish a low temperature for the strontium without unduly
lowering the temperature for the star in general. The observation of
stationary strontium lines would materially strengthen this argument,
[Pg 172]
but they have not so far been recorded. The fact that the strontium
stars are scattered, and not concentrated in any one part of the sky,
reduces the probability of this suggestion.
(3) Abnormal Abundance.—Abnormal abundance has been
progressively abandoned as an explanation of the various phenomena of
stellar spectra, and that it is the true interpretation of strontium
peculiarities seems somewhat unlikely. For the silicon stars, unusual
abundance is probably an untenable hypothesis, since the great strength
of the Si+ lines is apparently not accompanied by increase in the
silicon line, which should presumably occur if pure abundance is the
cause of the increased strength of the ionized silicon lines. Abnormal
strength of silicon in the cooler stars, doubly ionized silicon in the
early stars, or triply ionized silicon in the
stars, has not
been observed, and it is not very probable that, if silicon is unevenly
distributed in the universe, the irregularity would be revealed in
stars at one temperature only.
Such considerations point to the problem of the silicon and strontium
stars as one involving the atom and its energy supply, rather than an
abnormal distribution of the element in question. It is likely that the
problem of classifying the stars will be elucidated by a more
detailed study of the silicon and strontium lines. The behavior of
strontium appears, however, in some cases, to warrant the description
of “abnormal,” and it may be that the first step in the
star
problem will be the elimination from the general classification of
spectra such as those of the strontium stars. The present writer
inclines to the belief that the silicon and strontium stars will be
included in the normal
star classification, when such a one is
satisfactorily devised.
(e) Peculiar Class Stars.—Among the
stars there are
three which appear to be of special interest.
The star Andromedae, designated
in the Draper
Catalogue, has been shown to display enhanced lines of manganese,
broadly winged, and of unusual strength.[465]
[Pg 173]
The star Canum Venaticorum has been the subject of extensive
work.[466][467] The chief point of interest concerning it is the
occurrence of lines ascribed to the rare earths.[468] The spectra of
these elements are so rich in lines that spurious coincidences are
certain to occur, but comparisons with the spectrum of
Cygni
and of the chromosphere suggest that the strongest lines of europium
and terbium are indeed represented. From general ionization principles
it would appear that enhanced spectra are probably involved, but until
series relations are known it is not possible to discuss the subject
further.
The super-giant, or c-star, Cygni, Class
, has
probably greater possibilities for the stellar spectroscopist than any
other star, as its spectrum is peculiarly rich in fine sharp lines,
many of which are unidentified,
Cygni is representative of
a large class of stars, but it is the only one of them that has an
apparent magnitude bright enough to render it readily accessible. The
spectrum has been tabulated by Lockyer[469] and by Wright.[470] At the
temperatures concerned, the doubly enhanced lines of the metals are to
be anticipated, and it is probable that many of the faint unidentified
lines in the spectrum of this star are those of twice ionized metallic
atoms. The strongest doubly enhanced lines of the metals fall, as is
well known, in the ultra-violet,
Cygni contains the lines of
the
series of neutral helium, the most persistent lines
of the element, and this is significant in view of the extremely low
pressure that is assigned to the atmosphere of the star on the basis of
absolute magnitude.
THE C-STARS
The c-characteristic was first used by Miss Maury[471] to designate
stars, found in several spectral classes, that have marked spectral
peculiarities. The intensities of some of the metallic lines, chiefly
[Pg 174]
those of ionized atoms, are greatly strengthened for the class, and
other lines, chiefly those of the neutral atom, are weakened. The
band becomes markedly discontinuous, and heavy blends at 4072, 4077,
become conspicuous. The spectrum of a c-star is unmistakable in
appearance.
| Wave Lenght |
Wave Lenght |
Atom | Series | Wave Lenght |
Wave Lenght |
Atom | Series |
|---|---|---|---|---|---|---|---|
| 3758.8 | 3757.68 | Ti+ | 4325.2 | 4314.98 | Ti+ | ||
| 3759.30 | Ti+ | 4321.1 | Ti+ | ||||
| 3856.2 | 4337.6 | 4337.92 | Ti+ | ||||
| 3863.2 | 4374.7 | Ti+? | |||||
| 3900.7 | 3900.53 | Ti+ | 4395.3 | 4395.04 | Ti+ | ||
| 3913.6 | 3913.45 | Ti+ | 4400.2 | 4399.77 | Ti+ | ||
| 4003.0 | 4002.09 | Fe+ | 4417.9 | 4417.71 | Ti+ | ||
| 4009.4 | 4444.0 | 4443.80 | Ti+ | ||||
| 4012.6 | 4012.40 | Ti+ | 4450.6 | 4450.49 | Ti+ | ||
| 4024.8 | 4025.13 | Ti+ | 4469.5 | 4468.14 | Ti+ | ||
| 4028.5 | 4028.35 | Ti+ | 4471.8 | 4472.93 | Fe+ | ||
| 4030.8 | 4409.6 | 4489.21 | Fe+ | ||||
| 4053.8 | 4053.84 | Ti+ | 4491.6 | 4491.41 | Fe+ | ||
| 4077.9 | 4077.71 | Sr+ | 4501.5 | 4501.27 | Ti+ | ||
| 4122.8 | 4122.64 | Fe+ | 4508.5 | 4508.29 | Fe+ | ||
| 4128.1 | 4128. | Si+ | 4515.4 | 4515.34 | Fe+ | ||
| 4131.4 | 4131. | Si+ | 4520.3 | 4520.24 | Fe+ | ||
| 4143.9 | 4522.9 | 4522.64 | Fe+ | ||||
| 4173.6 | 4173.47 | Fe+ | 4534.2 | 4533.97 | Ti+ | ||
| 4179.5 | 4178.87 | Fe+ | 4534.17 | Fe+ | |||
| 4l87.6 | 4556.0 | 4555.90 | Fe+ | ||||
| 4215.7 | 4215.52 | Sr+ | 4558.9 | ||||
| 4233.6 | 4233.16 | Fe+ | 4564.0 | 4563.77 | Ti+ | ||
| 4271.7 | Fe+? | 4584.0 | 4583.84 | Fe+ | |||
| 4288.1 | 4287.88 | Ti+ | 4586. | ||||
| 4294.3 | 4294.10 | Ti+ | 4619.2 | 4620.52 | Fe+ | ||
| 4297.1 | 4296.56 | Fe+ | 4629.9 | 4629.33 | Fe+ | ||
| 4314.4 | 4312.88? | Ti+ | 4657.0 |
The foregoing tabulation contains a list of the lines that are strongly enhanced in the spectra of the c-stars. Successive columns give the approximate wave-length, taken from Miss Maury’s original list, the [Pg 175] laboratory wave-length of the line with which the stellar line is identified, the atom, and the series relations.
The preponderating characteristic lines are clearly those of ionized iron and ionized titanium.[472] All the strong lines of these atoms are found in the c-star spectrum, and they are there stronger than in any other class. It is found that spectra possessing the c-character have in general unusually sharp and narrow lines. It is probable that the lines in the spectrum of a c-star are actually stronger, as well as sharper, than the corresponding lines in a star of the same class and lower luminosity.[473]
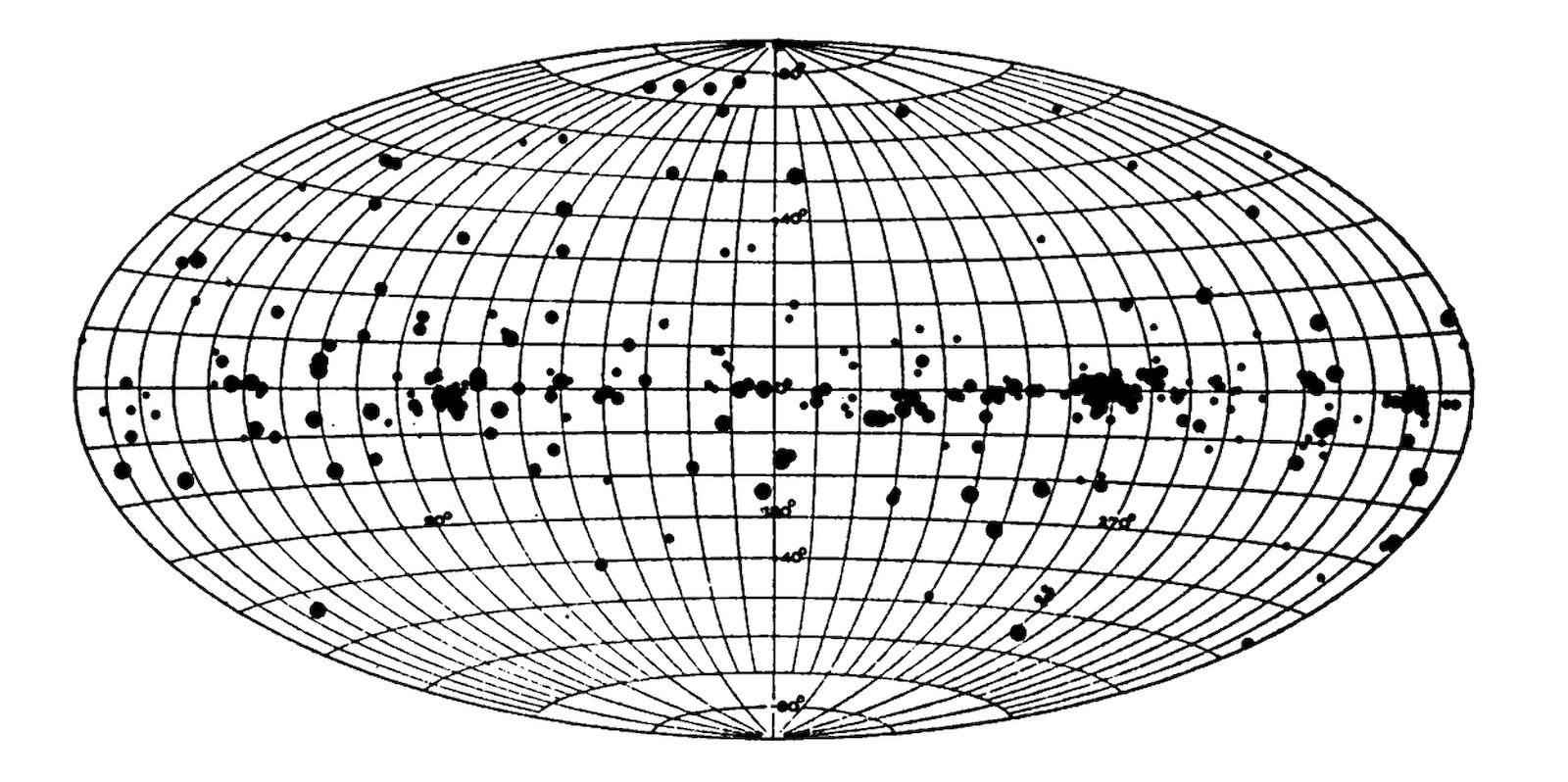
Figure 9
Galactic distribution of stars mentioned in the Draper Catalogue as having narrow lines. Four sizes of dots indicate stars of different apparent magnitudes; brighter than 5.0; 5.0-6.0; 6.0-8.0; and fainter than 8.0, respectively.
This phenomenon is connected with the question of the effective optical depth of the photosphere, and is discussed in Chapter IX.
It was first pointed out by Hertzsprung[474] that the c-character marks out a class of stars with distinct physical properties—extremely small parallaxes and proper motions, strong galactic concentration, and, accordingly, very high luminosity and volume, and low density. The [Pg 176] last feature furnishes an interpretation of the spectral peculiarities (see Chapter X).
The reality of the c-character has been questioned owing to a
misapprehension as to its criteria.[475] Fine lines always accompany
the c-character, but they may be present without it. The star h Ursae
Majoris is a case in point. It is listed in the Henry Draper Catalogue
as having narrow lines, a remark that usually indicates the presence
of the c-character. Actually the star appears to be a dwarf, of Class
, with considerable proper motion. Although the lines are narrow
and sharp, the spectrum has not the very typical appearance of a c-star.
[439] E. B. Wilson and Luyten, Proc. N. Ac. Sci., 11, 133, 1925.
[440] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 287, 1924.
[441] Shapley and H. H. Wilson, H. C. 271, 1925.
[442] Van Maanen, Proc. N. Ac. Sci., 4, 394, 1918.
[443] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 147, 183, 269, 1922.
[444] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 287, 1924.
[445] Ast. and Ap., 13, 448, 1894.
[446] H. A. 28, 1900.
[447] Lick Pub., 13, 248, 1918.
[448] H. H. Plaskett, Pub. Dom. Ap. Obs., 1, 325, 1922.
[449] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 287, 1924.
[450] Payne, H. C. 263, 1924.
[451] Payne, H. C. 263, 1924.
[452] Preface, Henry Draper Catalogue.
[453] M. N. R. A. S., 83, 403, 1923.
[454] H. C. 258, 1924.
[456] Shapley, H. B. 805, 1924.
[457] Shapley, Rep. Spectr. Class. Com., I. A. U., 1925.
[459] Mt. W. Contr. 244, 1922; 262, 1923.
[460] H. C. 264, 1924; cf. Lindblad, Ap. J., 59, 305, 1924.
[461] Shapley, H. B. 798, 1924; Luyten, H. C. 251, 1924.
[462] Rep. Spectr. Class. Com., I. A. U., 1922.
[463] Luyten, H. B. 797, 1924.
[464] J. S. Plaskett, Pub. Dom. Ap. Obs., 2, 335, 1924.
[465] Lockyer and Baxandall, Proc. Roy. Soc., 77A, 550, 1906.
[466] Belopolsky, Pub. Ac. Imp. St. Pet., 6, 12, 1913; Pulk. Bul., 6, 10, 1915.
[467] Lockyer and Baxandall, Proc. Roy. Soc., 77A, 550, 1906.
[468] Kiess, Pub. Obs. Mich., 3, 106, 1923.
[469] Lockyer, Pub. Sol. Phys. Com., 1904.
[470] Wright, L. O. B. 332, 1921.
[471] A. C. Maury, H. A., 28, 79, 1897.
[472] Russell, Ap. J., in press.
[473] Stewart, Phys. Rev., 22, 324, 1923; Russell and Stewart, Ap. J., 59, 197, 1924.
[474] A. N., 179, 374, 1908; A. N., 192, 262, 1912.
[475] Harper and Young, J. R. A. S. Can., 18, 9, 1924.
[Pg 177]
THE relative frequency of atomic species has for some time been of recognized significance. Numerous deductions have been based upon the observed terrestrial distribution of the elements; for example, attention has been drawn to the preponderance of the lighter elements (comprising those of atomic number less than thirty), to the “law of even numbers,” which states that elements of even atomic number are far more frequent than elements of odd atomic number, and to the high frequency of atoms with an atomic weight that is a multiple of four.
The existence of these general relations for the atoms that occur in the crust of the earth is in itself a fact of the highest interest, but the considerations contained in the present chapter indicate that such relations also hold for the atoms that constitute the stellar atmospheres and therefore have an even deeper significance than was at first supposed. Data on the subject of the relative frequency of the different species of atoms contain a possible key to the problem of the evolution and stability of the elements. Though the time does not as yet seem ripe for an interpretation of the facts, the collection of data on a comprehensive scale will prepare the way for theory, and will help to place it, when it comes, on a sound observational basis.
The intensity of the absorption lines associated with an element immediately suggests itself as a possible source of information on relative abundance. But the same species of atom gives rise simultaneously to lines of different intensities belonging to the same series, and also to different series, which change in intensity relative to one another according to the temperature of the star. The intensity of the absorption line is, of course, a very complex function of the temperature, the pressure, and the atomic constants—a matter [Pg 178] that has been discussed in detail in the preceding seven chapters.
The observed intensity can therefore be used directly for only a crude estimate of abundance. Roughly speaking, the lines of the lighter elements predominate in the spectra of stellar atmospheres, and probably the corresponding atoms constitute the greater part of the atmosphere of the star, as they do of the earth’s crust. Beyond a general inference such as this, few direct conclusions can be drawn from line-intensities. Russell[476] made the solar spectrum the basis of a discussion in which he pointed out the apparent similarity in composition between the crust of the earth, the atmosphere of the star, and the meteorites of the stony variety. The method used by him should be expected, in the light of subsequent work, to yield only qualitative results, since it took no account of the relative probabilities of the atomic states corresponding to different lines in the spectrum.
UNIFORMITY OF COMPOSITION OF THE STELLAR ATMOSPHERE
The possibility of arranging the majority of stellar spectra in homogeneous classes that constitute a continuous series, is an indication that the composition of the stars is remarkably uniform—at least in regard to the portion that can be examined spectroscopically. The fact that so many stars have identical spectra is in itself a fact suggesting uniformity of composition; and the success of the theory of thermal ionization in predicting the spectral changes that occur from class to class is a further indication in the same direction.
If departures from uniform distribution did occur from one class to another, they might conceivably be masked by the thermal changes of intensity. But it is exceedingly improbable that a lack of uniformity in distribution would in every case be thus concealed. It is also unlikely, though possible, that a departure from uniformity would affect equally and solely the stars of one spectral class. Any such departure, if found, would indicate that the presence of abnormal quantities of certain elements was an effect of temperature. This [Pg 179] explanation appears, however, to be neither justified nor necessary; there is no reason to assume a sensible departure from uniform composition for members of the normal stellar sequence.
MARGINAL APPEARANCE OF SPECTRUM LINES
Fowler and Milne[477] pointed out that the “marginal appearance,” when the line is at the limit of visibility, is a function of the abundance of the corresponding atom. For this reason their own theory, which dealt not with the marginal appearance but with the maximum of an absorption line, was capable of a more satisfactory observational test than Saha’s. It is possible, as shown below, to extend the Fowler-Milne considerations and to use the observed marginal appearances as a measure of relative abundance.
The conditions for marginal appearance must first be formulated. When a strong absorption line is at maximum, the light received from its center comes from the deepest layer that is possible for the corresponding frequency. The actual depth depends, as was pointed out in Chapter IX, upon the number of absorbing atoms per unit volume, and upon the atomic absorption coefficient for the frequency in question. The suggestions that were put forward in the chapter just quoted indicate that different lines, at their maxima, arise from different “effective levels,” the more abundant atoms appearing, other things being equal, at higher levels.
As an absorption line is traced through the classes adjacent to the one at which it attains maximum, it begins to diminish in intensity, owing to the decrease in the number of suitable atoms. If the line is very intense, the first effect of the fall in the number of suitable atoms is a reduction in the width and wings. As the number of suitable atoms per unit volume decreases further, a greater and greater thickness of atmosphere is required to produce the same amount of absorption, and accordingly the line originates deeper and deeper in the atmosphere of the star. As the “effective level” falls, the temperature of the [Pg 180] layer that gives rise to the line increases, owing to the temperature gradient in the stellar reversing layer. The observed fall in the intensity of the line is caused both by the reduction in the number of suitable atoms, and by the decreased contrast between the line and the background. The former cause predominates for strong (saturated) lines, and the latter for weak (unsaturated) lines.
As the atoms suitable to the absorption of the line considered decrease
in number, the effective level from which the line takes its origin
falls, and ultimately coincides with the photosphere (the level at
which the general absorption becomes great enough to mask
the selective absorption due to individual atoms). The line
then disappears owing to lack of contrast. Immediately before the
line merges into the photosphere (the approximate point estimated
as “marginal appearance”), all the suitable atoms above the
photosphere are clearly contributing to the absorption; in other
words the line is unsaturated. The position in the spectral
sequence of the marginal appearance of a line must then depend directly
.upon the number of suitable atoms above the photosphere;
considerations of effective level are eliminated. Hence a constant
is used on page 184.
The conditions at maximum and marginal appearance of a line in the spectral sequence are to some extent reproduced for an individual absorption line at the center of the line and at the edge of its wing. A hydrogen line displays wings that may extend to thirty Angstrom units on either side of the center. The energy contributing to the wings is evidently light coming from hydrogen atoms with a frequency that deviates somewhat from the normal. Atoms with small deviations are more numerous than atoms with large deviations, and therefore the light received from them originates in a higher effective level. The line center corresponds to the highest level of all. At points far out upon the wings, lower and lower levels are represented, until, where the line merges into the continuous background, the level from which it originates coincides with the photosphere, and the “marginal [Pg 181] appearance” of the line (if it may so be called) is reached. Accurate photometry of the centers and wings of strong absorption lines would seem to have an important bearing on the structure of the stellar atmosphere, as it would provide an immediate measure of the factor that produces the deviations from normal frequency. The success of parallel work in the laboratory[478] indicates that intensity distribution should be amenable to observation and to theory.
OBSERVED MARGINAL APPEARANCES
The spectral class at which a line is first or last seen is obviously, to some extent, a function of the spectroscopic dispersion used, for, with extremely small dispersion, many of the fainter lines fail to appear at all. A line will also probably appear somewhat later, and disappear somewhat earlier, with small than with large dispersion. It is therefore a matter of some difficulty to obtain measures of marginal appearance that shall be absolute, but the present discussion neither assumes nor requires them. The method used is designed for the estimation of relative abundances, and all that is required of the data is that they shall be mutually consistent.
In order to attain the maximum degree of consistency, the estimates used in this chapter were derived chiefly from the two series of plates mentioned in Chapter VIII. All the plates used were made with the same dispersion (two 150 objective prisms) and were of comparable density, and of good definition. The data furnished by the writer’s own measures were supplemented by some estimates derived by Menzel[479] from a similar series of plates, of the same dispersion and comparable quality. The estimate of the marginal appearance of potassium was very kindly suggested by Russell from solar observations.
The observed marginal appearances of all the lines that are available are summarized in the table that follows. Successive columns contain the atomic number and atom, the series relations, the wave-length of the line used, and the Draper classes at which the line is observed, [Pg 182] respectively, to appear, to reach maximum, and to disappear. Asterisks in the last column denote the ultimate lines of the neutral atom, which are strongest at low temperatures, and have no maximum.
| Atom | Series | Line | Classes | Atom | Series | Line | Classes | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | H | 4340 | - | - | 22 | Ti | 3999 | * | * | ||||
| 2 | He | 4471 | 4862 | * | * | ||||||||
| 5015 | 4867 | * | * | ||||||||||
| 4388 | 4856 | * | * | ||||||||||
| He+ | 4542 | - | 4536 | - | - | ||||||||
| 3 | Li | 6707 | * | * | - | 4535 | - | - | |||||
| 6 | C+ | 4267 | 23 | V | 4333 | * | * | ||||||
| 11 | Na | 5889 | * | * | 4330 | * | * | ||||||
| 5896 | * | * | 24 | Cr | 4290 | * | * | ||||||
| 12 | Mg | 5184 | - | ? | 4275 | * | * | ||||||
| 5173 | - | ? | 4254 | * | * | ||||||||
| 5167 | - | ? | 4497 | - | |||||||||
| 3838 | - | ? | 25 | Mn | 4034 | * | * | ||||||
| 3832 | - | ? | 4033 | * | * | ||||||||
| 3829 | - | ? | 4030 | * | * | ||||||||
| Mg+ | 4481 | - | 4084 | - | |||||||||
| 13 | Al | 3962 | * | * | 4041 | - | |||||||
| 3944 | * | * | 26 | Fe | 4325 | - | |||||||
| 14 | Si | 3905 | - | 4811 | |||||||||
| Si+ | 4128 | 30 | Zn | 4811 | |||||||||
| 4131 | 4722 | ||||||||||||
| 19 | K | 4044 | * | * | 38 | Sr | 4607 | * | * | ||||
| 4047 | * | * | Sr+ | 4078 | - | ||||||||
| 20 | Ca | 4227 | * | * | 54 | Ba+ | 4555 | - | ? | ||||
| 4455 | - | ||||||||||||
| Ca+ | 3933 | - | - | ||||||||||
[Pg 183]
Estimates by Menzel are indicated by a dagger; those marked by a double dagger were taken from dyed plates made with slightly smaller dispersion.
METHOD OF ESTIMATING RELATIVE ABUNDANCES
If the physical conception of marginal appearance above outlined is correct, the number of atoms of a given kind above the photosphere will practically determine the class at which the corresponding line is last seen.[480] Now at marginal appearance the number of suitable atoms is only a small fraction of the total amount of the corresponding element that is present in the reversing layer, and this fraction is precisely the “fractional concentration” evaluated by Fowler and Milne. If then it be assumed that the number of atoms required for marginal appearance is the same for all elements, the reciprocals of the computed fractional concentrations at marginal appearance should give directly the relative abundances of the atoms.
A few remarks concerning the underlying assumptions may be appropriate.
In applying the theory it is assumed that stellar atmospheres are of
uniform composition, and that at marginal appearance all lines are
unsaturated. These reasonable assumptions have been discussed above,
and they are here explicitly restated. The third assumption, that
the same number of atoms is represented at the marginal appearance
of a line, whatever the element, is by far the most serious. It
implies the equality of the absorbing efficiencies of the individual
atoms under the conditions involved. This is assumed in default of a
suitable correction, but it is not suggested that the use here made
of the assumption would imply its universal validity. Its present
application is made under conditions of extremely low pressure
(),
and over a range of temperature from 7000° to 10,000°. Under such
conditions the absorbing efficiency of an atom will depend almost
entirely upon its energy supply and upon its inherent tendency to
recover after undergoing an electron transfer. The pressures are so
low that collisions will have no appreciable effect in disturbing
the normal recovery of the atoms. The energy supply will vary with
the temperature; but with the range of temperature considered the
[Pg 184]
variation will probably not be very large. The reorganization time
of an atom appears to be an atomic constant, and to be of the same
order for all atoms hitherto examined in the laboratory or in stellar
atmospheres. As a working assumption, then, the equality of the
atomic absorption coefficients is assumed with some confidence in the
discussion of observed marginal appearances.
| Atomic Number | Atom | Atomic Number | Atom | Atomic Number | Atom | |||
|---|---|---|---|---|---|---|---|---|
| 1 | H | 11 | 13 | Al | 5.0 | 23 | V | 3.0 |
| 2 | He | 8.3 | 14 | Si | 4.8 | 24 | Cr | 3.9 |
| He+ | 12 | Si+ | 4.9 | 25 | Mn | 4.6 | ||
| 3 | Li | 0.0 | Si+++ | 6.0 | 26 | Fe | 4.8 | |
| 6 | C+ | 4.5 | 19 | K | 3.5 | 30 | Zn | 4.2 |
| 11 | Na | 5.2 | 20 | Ca | 4.8 | 38 | Sr | 1.8 |
| 12 | Mg | 5.6 | Ca+ | 5.0 | Sr+ | 1.5 | ||
| Mg+ | 5.5 | 22 | Ti | 4.1 | 54 | Ba+ | 1.1 |
As stated above, the relative abundances of the atoms are given
directly by the reciprocals of the respective fractional concentrations
at marginal appearance. The values of the relative abundance thus
deduced are contained in Table XXVIII. Successive columns give the
atomic number, the atom, and the logarithm of the relative abundance,
.
COMPARISON OF STELLAR ATMOSPHERE AND EARTH'S CRUST
The preponderance of the lighter elements in stellar atmospheres is a striking aspect of the results, and recalls the similar feature that is conspicuous in analyses of the crust of the earth.[481] A distinct parallelism in the relative frequencies of the atoms of the more abundant elements in both sources has already been suggested by Russell,[482] and discussed by H. H. Plaskett,[483] [Pg 185] and the data contained in Table XXVIII confirm and amplify the similarity.
A close correspondence between the percentage compositions of the stellar atmosphere and the crust of the earth would not, perhaps, be expected, since both sources form a negligible fraction of the body of which they are a part. There is every reason to suppose, on observational and theoretical grounds, that the composition of the earth varies with depth below the surface; and the theory of thermodynamical equilibrium would appear to lead to the result that the heavier atoms should, on the average, gravitate to the center of a star. If, however, the earth originated from the surface layers of the sun,[484] the percentage composition of the whole earth should resemble the composition of the solar (and therefore of a typical stellar) atmosphere. But the mass of the earth alone is considerably in excess of the mass of the reversing layer of the sun.[485] Eddington,[486] quoting von Zeipel,[487] has pointed out that an effect of rotation of a star will be to keep the constituents well mixed, so that the outer portions of the sun or of a star are probably fairly representative of the interior. Considering the possibility of atomic segregation both in the earth and in the star, it appears likely that the earth’s crust is representative of the stellar atmosphere.
The most obvious conclusion that can be drawn from Table XXVIII is that all the commoner elements found terrestrially, which could also, for spectroscopic reasons, be looked for in the stellar atmosphere, are actually observed in the stars. The twenty-four elements that are commonest in the crust of the earth,[488] in order of atomic abundance, are oxygen, silicon, hydrogen, aluminum, sodium, calcium, iron, magnesium, potassium, titanium, carbon, chlorine, phosphorus, sulphur, nitrogen, manganese, fluorine, chromium, vanadium, lithium, barium, zirconium, nickel, and strontium.
The most abundant elements found in stellar atmospheres, also in [Pg 186] order of abundance, are silicon, sodium, magnesium, aluminum, carbon, calcium, iron, zinc, titanium, manganese, chromium, potassium, vanadium, strontium, barium, (hydrogen, and helium). All the atoms for which quantitative estimates have been made are included in this list. Although hydrogen and helium are manifestly very abundant in stellar atmospheres, the actual values derived from the estimates of marginal appearance are regarded as spurious.
The absence from the stellar list of eight terrestrially abundant elements can be fully accounted for. The substances in question are oxygen, chlorine, phosphorus, sulphur, nitrogen, fluorine, zirconium, and nickel, and none of these elements gives lines of known series relations in the region ordinarily photographed.
The “triplets” of neutral oxygen, in the red, should
prove accessible in the near future; the point of disappearance of
these lines would not be difficult to estimate, and they would furnish
a value for the stellar abundance of oxygen. The lines of ionized
oxygen, which have not yet been analyzed into series, are conspicuous
in the
stars,[489] and the element is probably present in large
quantities.
Sulphur and nitrogen both lack suitable lines in the region usually studied; the analyzed spectrum of neutral sulphur is in the green and red,[490] or in the far ultra-violet,[491] and the neutral nitrogen spectrum has not as yet been arranged in series. Both sulphur and nitrogen appear, in hotter stars, in the once and twice ionized conditions,[492] and are probably abundant elements in stellar atmospheres.
For the remaining elements, phosphorus, chlorine, fluorine, zirconium and nickel, series relations are not, as yet, available. No lines of phosphorus or the halogens have been detected in stellar spectra, but these elements have not been satisfactorily analyzed spectroscopically, and their apparent absence from the stars is probably a result of a deficiency in suitable lines. Nickel and zirconium will probably be [Pg 187] analyzed in the near future; they are both well represented in stellar spectra, and nickel especially is probably abundant.
The relative abundances, in the stellar atmosphere and the earth, of the elements that are known to occur in both, display a striking numerical parallelism. Table XXIX gives the data for the sixteen elements most abundant in the stellar atmosphere. Successive columns give the atomic number, the atom, the relative stellar abundance, the relative terrestrial abundance (both for the lithosphere, hydrosphere, and atmosphere, and for the whole earth),[493] and the relative abundance in stony meteorites.[494]
| Atomic number | Atom | Stellar Abundance | Terrestrial Abundance | Abundance Stony Meteorites |
|
|---|---|---|---|---|---|
| Crust | Whole Earth | ||||
| 14 | Si | 5.7 | 16.2 | 9.58 | 11.2 |
| 11 | Na | 5.7 | 2.02 | 0.97 | 0.6 |
| 12 | Mg | 4.2 | 0.42 | 3.38 | 2.8 |
| 13 | A1 | 3.6 | 4.95 | 2.66 | 1.1 |
| 6 | C | 3.6 | 0.21 | .... | .... |
| 20 | Ca | 2.9 | 1.50 | 1.08 | 0.56 |
| 26 | Fe | 2.5 | 1.48 | 46.37 | 5.92 |
| 30 | Zn | 0.57 | 0.0011 | .... | .... |
| 22 | Ti | 0.43 | 0.241 | 0.12 | .... |
| 25 | Mn | 0.36 | 0.035 | 0.06 | .... |
| 24 | Cr | 0.29 | 0.021 | 0.05 | 0.29 |
| 19 | K | 0.11 | 1.088 | 0.38 | 0.10 |
| 23 | V | 0.05 | 0.0133 | .... | .... |
| 38 | Sr | 0.002 | 0.0065 | .... | .... |
| 54 | Ba | 0.005 | 0.0098 | .... | .... |
| 3 | Li | 0.0000 | 0.0829 | .... | .... |
The figures in the fifth column are derived from Clarke’s estimates of the percentage composition of the earth. The composition of the earth has been variously estimated by different investigators, and the [Pg 188] resulting figures depend upon theories that cannot be discussed here. The order given by Clarke is based on the assumption of a nickel-iron core.
The numbers expressing the stellar abundance are percentages, calculated on the assumption that the stellar and terrestrial elements form the same fraction of the total material present. This reduces the two columns of numbers to a form in which they are directly comparable, but no great importance is attached to the absolute percentages in the third column.
The method that has here been used is subject to inaccuracy and uncertainty, especially in the estimates of the exact spectral class at which a line is first or last seen. The most that can be expected is that the results will be trustworthy in order of magnitude. It may be seen that the only element for which the stellar and terrestrial values are not of the same order is zinc. Further, it appears that when the estimates for the percentage composition of the whole earth are used in the comparison with the stellar values, the agreement is improved in the case of silicon, magnesium, aluminum, manganese, chromium, and potassium; it is about the same for calcium and titanium, is less close for sodium, and markedly poorer for iron.[495] In the stellar atmosphere and the meteorite the agreement is good for all the atoms that are common to the two, but several important elements are not recorded in the meteorite.
The outstanding discrepancies between the astrophysical and terrestrial abundances are displayed for hydrogen and helium. The enormous abundance derived for these elements in the stellar atmosphere is almost certainly not real. Probably the result may be considered, for [Pg 189] hydrogen, as another aspect of its abnormal behavior, already alluded to;[496] and helium, which has some features of astrophysical behavior in common with hydrogen, possibly deviates for similar reasons. The lines of both atoms appear to be far more persistent, at high and at low temperatures, than those of any other element.
The uniformity of composition of stellar atmospheres appears to be an established fact. The quantitative composition of the atmosphere of a star is derived, in the present chapter, from estimates of the “marginal appearance” of certain spectral lines, and the inferred composition displays a striking parallel with the composition of the earth.
The observations on abundance refer merely to the stellar atmosphere, and it is not possible to arrive in this way at conclusions as to internal composition. But marked differences of internal composition from star to star might be expected to affect the atmospheres to a noticeable extent, and it is therefore somewhat unlikely that such differences do occur.
[476] Russell, Science, 39, 791, 1914.
[477] R. H. Fowler and Milne, M. N. R. A. S., 83, 403, 1923.
[478] Harrison, unpub.
[479] H. C. 258, 1924.
[480] Payne, Proc. N. Ac. Sci., 11, 192, 1925.
[481] Clarke and Washington, Proc. N. Ac. Aci., 8, 108, 1922.
[482] Russell, Science, 39, 791, 1914.
[483] Pub. Dom. Ap. Obs., 1, 325, 1922.
[484] Jeffreys, The Earth, 1924.
[485] Shapley.
[486] Nature, 115, 419, 1925.
[487] M. N. R. A. S., 84, 665, 1924.
[488] Clarke and Washington, Proc. N. Ac. Sci., 8, 108, 1922.
[489] H. C. 256, 1924.
[490] Fowler, Report on Series in Line Spectra, 170, 1922.
[491] Hopfield, Nature, 112, 437, 1923.
[492] H. C. 256, 1924.
[493] Clarke, U. S. Geol. Surv. Prof. Pap. 132, 1924.
[494] G. P. Merrill, quoted by Clarke, U. S. Geol. Surv. Bul. 491.
[495]
Professor Russell believes that iron is much more
abundant, at least in the sun, than calculated above. He writes: “More
than half of all the strong winged solar lines are iron lines, and the
strength and evident saturation of even the faint satellites in the
iron multiplets is remarkable.... There are a great many multiplets
of nearly equal strength arising from the low triplet level in
iron.... Nothing like this happens for the
lines, or for
and
, although it may hold true for the Mg triplets. I should
consequently favor multiplying the percentage for iron by a factor
of at least 3 and probably 5—which would put it where it obviously
belongs.”
[Pg 190]
IT is not necessary to discuss the possibility or desirability of classifying stellar spectra. Both have been adequately demonstrated by Miss Cannon in the Henry Draper Catalogue,[497] which contains the classification that has been accepted as standard.[498] The catalogue will undoubtedly long remain the authoritative source of spectral data for the major part of the stars bright enough to be accessible to the spectroscopist. The uses of the material that it contains are so numerous and so direct that the basis and meaning of the classes seem to deserve attention.
In classifying a number of objects, an attempt should be made to select criteria that will distribute the material into the most natural groups. A classification devised with one point of view will not necessarily appear natural from another, and the best that can generally be done is to select the standpoint that seems to be the most important. From all other standpoints the classification is empirical, and must be treated as such. It seems necessary to emphasize this empiricism with regard to the classifying of stellar spectra, for reference is often made to the Henry Draper Classification as though it had a theoretical, even an evolutionary, basis, whereas it is essentially arbitrary. It is true that a classification based on theoretical principles is very desirable, but at present there is no adequate physical theory on which to found one.
The essential feature of the Draper classification is that it aims at classing together similar spectra, relying on general appearance, and not on the measurement of any one line or group of lines. This has the advantage of distributing the material in the most natural groups possible, and a disadvantage in that different observers may find it [Pg 191] difficult to be sure that their criteria are identically weighted.
That the original aim was empirical and not theoretical is clear from the introduction to the first extensive list of spectra classified according to the Draper system:[499] “It was deemed best that the observer should place together all stars having similar spectra and thus form an arbitrary classification rather than be hampered by any preconceived theoretical ideas.” The present classification was the natural outcome of such a procedure. As A. Fowler has remarked,[500] “the Draper classification is based essentially on the observed spectral lines, and in reality may be regarded as independent of any other consideration whatsoever. Even if we did not know the origin of a single line in the stellar spectra, it is probable that we should have arrived at precisely the same order.”
The descriptions that are contained in the preface to the Henry Draper Catalogue, and which have long been classical, were designed to describe the salient features of the groups that had been formed. It is only in a somewhat restricted sense that they constitute the criteria for those groups. The descriptions were compiled from the spectra of apparently bright stars of the classes involved, but the greater number of the spectra actually classified are taken with such short dispersion that all except the very strongest lines are difficult to distinguish, and are certainly not susceptible of accurate measurement. This fact should affect the standpoint of those who criticize the “multiple nature” of the Draper criteria. A portion of one of the plates used in the classification is herewith reproduced with no magnification. This photograph should make it apparent to anyone familiar with the use of spectra that the classification of stars is very largely a practical problem.
Instead, then, of examining the possible merits of the best theoretical classification system, it appears to be more useful to examine the physical implication of the most representative classification that it has been found possible to make in practice. The fact that the Draper [Pg 192] system is so representative has been regarded as one of its great merits, and has rightly placed it in the authoritative position that it occupies.
When a group of stars is being studied for a special purpose, it is often found that the Draper classes are not fine enough to subdivide the material usefully. In such cases reclassification is often essential. It has sometimes been suggested that this indicates that the Draper classes are inadequate; but it must be recollected that, for the greater part of the material contained in the Catalogue, finer classification would have been impossible, and the subclasses in use today represent the practical survival from a far larger number, which were originally thought to be usable. Actually the stars represent a continuous gradation from class to class, and in classifying it is only possible to use the smallest distinguishable steps, which will obviously be smaller, the larger the dispersion. When it is found necessary to reclassify the stars more finely in a special investigation, as in the Harvard or Mount Wilson work on spectroscopic parallaxes,[501] one or more measurable criteria are selected and used as a basis, but standard stars classified at Harvard are used to define the scale. These measured or closer classifications, while essential for the purpose for which they were designed, have no theoretical advantage over the Draper system (on which they are ultimately founded), and do not, as is sometimes inferred,[502] indicate that the latter is in error.
Although devised with no theoretical basis, the Draper classification has long been recognized as classifying something physical, and the fact that the majority of the stars had been ranged by it in a single sequence suggested that a single variable was principally involved. From general theoretical considerations it could have been predicted that this variable was probably the temperature, but, in addition, the observational evidence that this was the case was immediately convincing. In the words of A. Fowler,[503] “... the typical stars not only increase in redness in passing through the sequence, but successive Draper classes correspond to nearly equal increments of redness as measured by the color index.”
[Pg 193]
The preceding eight chapters review the arguments and the observations
that have established the connection between the spectrum of a star and
its temperature. From an examination of the data there given it becomes
clear that what the Draper system classifies is essentially the degree
of thermal ionization. A. Fowler, in fact, makes the illuminating
distinctions of “arc” ( to
), “spark” (
to
), and
“superspark” (
onwards) stars.
The table that follows contains, in concise form, the chief features by which the type stars of each class are to be recognized, although it is again emphasized that these were not actually measured as criteria for the Draper classes. The lines characteristic of each class serve, however, to specify its degree of thermal ionization.
The homogeneity of the spectra in a given class is striking, and the fact that large numbers of stars display exactly similar spectra has a significance—considered in another chapter[504]—to which the classification problem cannot do more than call attention. The similarity of the spectra becomes the more striking when it is remembered that the range of conditions embraced within any one class is very wide; the ratio in mean density may be as great as 10[505] between stars of the same class but of differing absolute magnitude.[506]
[Pg 194]
The close spectral similarity between, giants and dwarfs, in spite of the great differences in physical conditions, should not, however, be misinterpreted. The observed facts are in exact accordance with what might have been anticipated. In the first place, thermal ionization is governed by the surface gravity, and only indirectly by the mean density.[507]
| Class | Characteristic Lines | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O | H | He | Si+++ | C++ | N++ | He+ | |||||||||
| H | He | Si+++ | He+ | O+ | |||||||||||
| H | He | Si+++ | O+* | ||||||||||||
| H | He* | ||||||||||||||
| H | He | ||||||||||||||
| H | He | Si+ | Ca+ | ||||||||||||
| H | He | Si+ | Ca+ | Mg+ | |||||||||||
| H | He | Si+ | Ca+ | Mg+ | |||||||||||
| H* | Si+* | Ca+ | Mg+ | ||||||||||||
| H | Ca+ | Mg+* | Ca | Fe | |||||||||||
| H | Ca+ | Mg+ | Ca | Fe | |||||||||||
| H | Ca+ | Ca | Fe | Ti | |||||||||||
| H | Ca+ | Ca | Fe | Ti | |||||||||||
| H | Ca+ | Ca | Fe | Ti | G bd. | ||||||||||
| H | Ca+ | Ca | Fe | Ti | G bd. | ||||||||||
| H | Ca+ | Ca | Fe | Ti | G bd. | ||||||||||
| H | Ca+* | Ca | Fe* | Ti* | G bd.* | ||||||||||
| H | Ca+ | Ca* | Fe | Ti | TiO₂ | ||||||||||
| H | Ca+ | Ca | Fe | Ti | TiO₂ | ||||||||||
| H | Ca+ | Ca | Fe | Ti | TiO₂ | ||||||||||
The division into “arc,” “spark,” and “superspark” is clearly shown by the table. Maxima of the lines which are used as criteria of class are marked with an asterisk.
[Pg 195]
It is shown in Chapter III that the range in surface gravity is far smaller than the range in mean density. Secondly, the basis of the classification has been shown to be the degree of thermal ionization.[508] Granted that the value of the partial electron pressure is low enough, in dwarfs as well as in giants, for thermal ionization to predominate over ionization by collision, a mass of gas will pass through the same succession of ionization-stages with changing temperature, whatever the surface gravity. Any given stage of ionization will, however, be reached at a lower temperature, the lower the pressure, since, as pointed out in Chapter X,[509] lowered pressure tends to increase the degree of ionization, and will help to produce a given degree of ionization at a lower temperature.
The Draper system takes no direct account of temperature. It classifies purely by degree of ionization, and therefore, as it relates to atmospheres in which the surface gravities differ widely, it will produce classes that are not homogeneous in temperature; dwarfs will be hotter than giants of the same spectral class. Fowler and Milne[510] anticipated a difference of from 10 to 20 per cent, and differences in this sense and of this order actually occur.[511] Physically it seems to be more important to class together stars having the same atmospheric properties than stars at exactly the same effective temperature, although the latter might conceivably be better suited to some purposes.
Although giant and dwarf stars may be found with very similar spectra,
it is well known that they display important differences for individual
lines, and these differences have formed the basis for the estimation
of spectroscopic parallaxes.[512] If the spectrum of a giant star is
compared with the spectrum of a dwarf of the same temperature,
the two will be found to differ. The line-intensities in the spectrum
of the dwarf will place it in a spectral class nearer to the red end
of the sequence—if the giant is of Class , the dwarf may be a
star. There are two ways in which the stars might be brought
into the same spectral class; by an alteration of temperature or by
an alteration of pressure. If the temperature of the dwarf star were
[Pg 196]
raised, the resulting changes in ionization in its atmosphere would
produce changes in the intensities of the lines in the spectrum.
At some temperature, about 15 per cent higher than the original
temperature of the dwarf star, it would give a spectrum resembling that
of the giant.
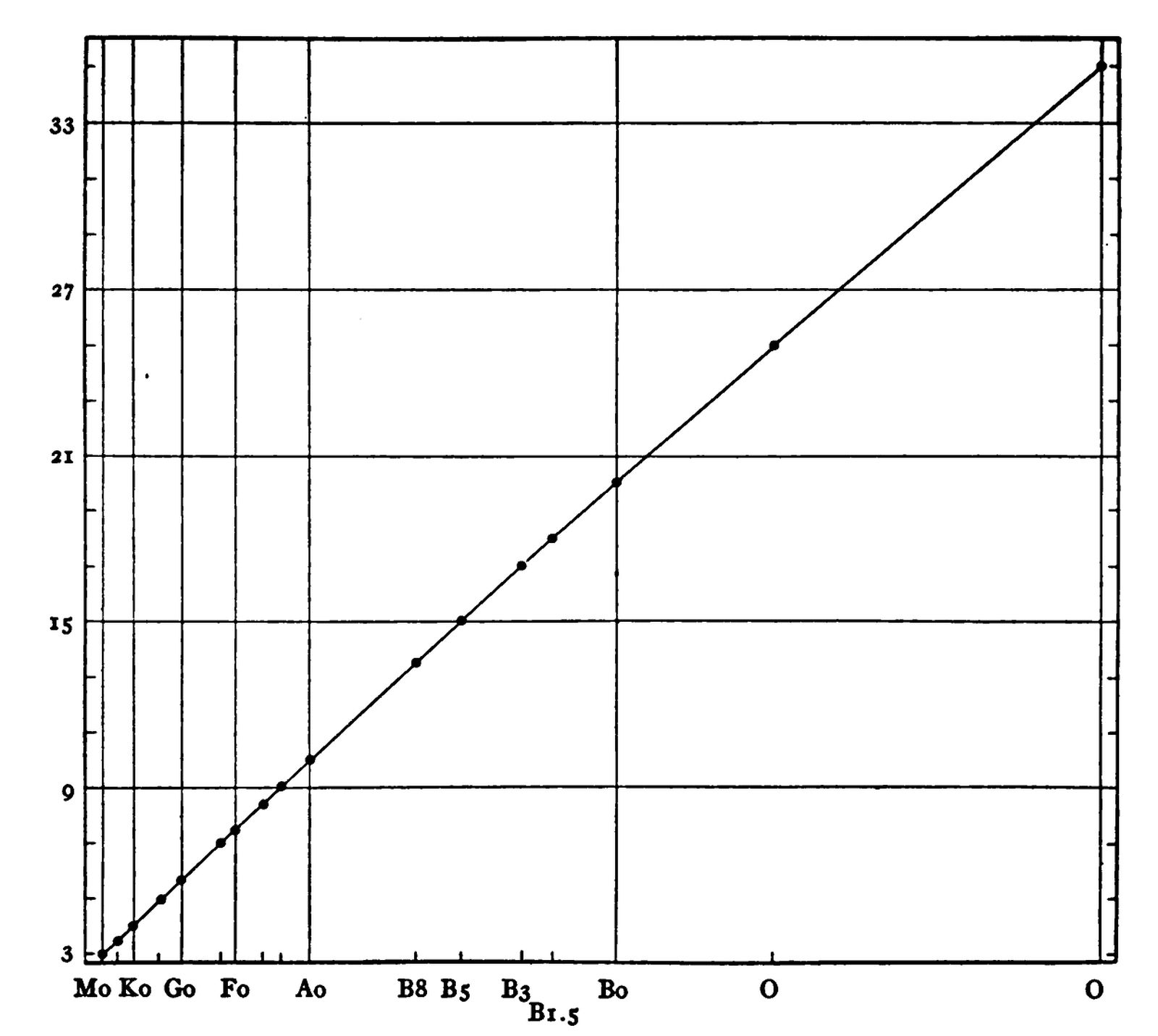
Figure 10
Schematic representation of the ionization temperature scale for the
sequence of stellar classes. Ordinates are absolute temperatures
in thousands of degrees; abscissae are Draper classes. The points
representing the different classes have been made to lie on a straight
line, so that the temperature range of the corresponding classes shall
appear along the axis of abscissae. Vertical lines are drawn through
,
,
,
,
,
, and the upper
limit of the
class, in order to show the increase in temperature
range for the hotter classes.
If the pressure in the atmosphere of the dwarf star were reduced, the resulting increase in the degree of ionization would also produce changes in the spectral lines, until it gave a spectrum similar to that of the giant. There is, however, no reason to suppose that the [Pg 197] changes produced in the intensities of individual lines by these temperature and pressure changes would be in all cases exactly equal, although they would in general operate in the same direction.
| Class | Effective Temperature |
Absolute Magnitude | Galactic Concentration |
Percent in H. D. C. |
Space Number | ||
|---|---|---|---|---|---|---|---|
| d | g | 7.0-8.25 | 17.0 | ||||
| 20,000° | |||||||
| to | -0.50 | 3.52 | }4.4 | ||||
| 15,000 | |||||||
| 16 | 0.96 | ||||||
| 50. | 9.2 | 4.70 | |||||
| 11,200 | 12.8 | 3.5 | 10.41 | }250 | |||
| +1.50 | 5.3 | 1.8 | 8.89 | ||||
| 2.8 | 1.2 | ||||||
| 8,600 | +2.20 | 1.9 | 1.9 | 2.31 | |||
| 7,000 | +2.5 | 1.6 | 1.8 | 5.48 | }680 | ||
| +2.9 | 1.2 | 1.4 | 3.37 | ||||
| 6,080 | +3.5 | 1.3 | 1.0 | 5.98 | |||
| +4.2 | 4.28 | }7600 | |||||
| 5,460 | +4.5 | -1.5 | 4.78 | ||||
| 4,820 | +4.8 | +0.6 | 8.98 | ||||
| 4,240 | +6.20 | +1.05 | 19.65 | }160 (giant) | |||
| 6.85 | |||||||
| 3,600 | +7.20 | +0.50 | 4.80 | }22 (giant) | |||
| 3,380 | + 10.20 | +0.40 | 2.10 | ||||
Excitation and ionization conditions differ so widely for different atoms that it would be expected that two factors, one of which encourages ionization, while the other discourages recombination, would not in every case balance exactly, even when their mean effect was constant, as it is for any one Draper class.
The Henry Draper Catalogue, as we have emphasized, was made on the basis of the general resemblance of the spectra, an arrangement which corresponds to the greatest physical homogeneity that can be obtained. As regards features of their spectra, it is therefore to be expected that the members of any one class will correspond closely, and care [Pg 198] must be exercised in eliminating redundancies from discussions of the homogeneity of the individual classes.
There are, however, other types of discussion, independent of spectroscopic data, and such investigations have shown that the Draper classes have indeed a significance far beyond the mere formation of homogeneous groups of spectra. In illustration of the profound statistical significance of the classification, the table on page 197 of the present chapter contains a brief synopsis of some of the most salient features that have been correlated with spectral class. Successive columns contain the class, the effective temperature,[513] the mean absolute magnitude,[514] the galactic concentration,[515] the percentage of the class in the Draper catalogue,[516] and the computed number per million cubic parsecs.[517]
[497] H. A., 91-99.
[498] Rep. I. A. U., Rome, 1922.
[499] H. A., 28, 131, 1901.
[500] Observatory, 38, 381, 1915.
[501] Mt. W. Contr. 199, 1918.
[502] Harper and Young, J. R. A. S. Can., 18, 9, 1924.
[503] Observatory, 38, 381, 1915.
[505] Observatory, 38, 381, 1915.
[510] M. N. R. A. S., 83, 403, 1923.
[512] Adams and Joy; Mt. W. Contr. 142, 1917.
[513] A. N., 219, 361, 1923.
[514] Lundmark, Pub. A. S. P., 34, 147, 1922.
[515] Shapley, H. B. 796, 1924.
[516] Shapley and Cannon, Proc. Am. Ac. Sci., 59, 217, 1924.
[517] Shapley and Cannon, ibid., 59, 230,1924.
[Pg 199]
THE future of a subject is the product of its past, and the hopes of astrophysics should be implicit in what the science has already achieved. Astrophysics is a young science, however, and is still, to some extent, in a position of choosing its route; it is very much to be desired that present effort should so be directed that the chosen path may lead in a permanently productive direction. The direction in which progress lies will depend on the material available, on the development of theory, and on the trend of thought.
The material already at hand is far from exhaustively analyzed, and it is perhaps premature to contemplate collecting more. But as a science progresses it is often possible to direct the way “by showing the kind of data which it is especially important to improve,” and particularly is this the case for astrophysics. In the improvement of the old data, by far the most important requirement is some method of standardizing the intensities of spectrum lines, and of measuring their width, energy distribution, and central intensity. This involves a very difficult and necessary piece of photographic photometry. The problem is an old one that has defied attack for a long time past. It is none the less urgent, and until the attack has been successfully made, many questions, such as are discussed in Chapter III, and other questions, which, for lack of data, we have not been able to discuss at all, must await their precise answers.
Much patient labor, on types of investigation that have already been well worked, still remains to be done. The identification of lines in the spectra of the sun and stars must necessarily be of a laborious nature, but the fact that more than two thirds of the lines in Rowland’s table are still unidentified shows how necessary and how [Pg 200] large a piece of work this is. One of the things that would greatly assist progress would be a revision of Rowland’s table in the light of the recent analysis of the arc and spark spectra of the metals, insertion of the series relations, when known, and the reduction of the wave-length system to International Angstroms.
Another line of work, which lies upon the borderland between astrophysics and pure physics, is the analysis of spectral series. For most of the astrophysically important lines, series relations are already known, but some of the more difficult spectra, such as the spectrum of nitrogen, remain unanalyzed. The analysis of all such spectra is necessary to the advance of astrophysics.
The investigation of stellar spectra has been confined, for the most part, to the region lying between 3900 and 5000, although work on special stars has been carried into the red and the ultra-violet. The use of special dyes should permit work to be carried to about 7900 in the red, and a wave-length of 3500 appears to be accessible in the ultra-violet. There appears to be a large field for an extension of the analysis of stellar spectra into regions of the spectrum that are comparatively unexplored, and the writer hopes in the immediate future to undertake work in this direction.
The types of investigation hitherto mentioned are amplifications of work already in progress. New fields are not easy to predict, but they may be suggested by examining the extent to which present investigation is covering the possibilities of the data. The line position and intensity data are in full use at the present time. The form and energy distribution of individual lines, and the study of asymmetries, are among the urgent future problems. The measurement of the polarization of the light received from the stars has enormous possibilities, but so far very little success has attended such attempts.
The future progress of theory is a harder subject for prediction than the future progress of observation. But one thing is certain: observation must make the way for theory, and only if it does so can the science have its greatest productivity. Observational astrophysics [Pg 201] is so vigorous a science that the progress of theory is almost completely determined by the progress of observation.
The most important of the three factors contemplated at the opening of the chapter is perhaps the trend of thought. It is owing to the tendency towards laying stress on observation, and to the general lessening of the distrust of large dimensions, that astrophysics has become possible as a science. The surprising growth of the subject during the last forty years is in great measure the result of this happy chance. The growth of the subject during the next forty years will depend on the coming trend of thought.
[Pg 202]
The prospect appears encouraging. At the present time the tendency is towards mutual toleration of point of view and to understanding of limitations among the sciences, and a consequent increase of correlation. If the breadth of conception thus engendered develops in the future as it has done in the immediate past, there is hope that the high promise of astrophysics may be brought to fruition.
[Pg 203]
I. INDEX TO DEFINITIONS
AN attempt has been made to define specifically, at some point in the text, most of the technical terms that are associated with the theory of ionization. For convenience of reference, the most important of these terms are collected into the brief index which is given below. The references are to the pages on which the term is defined.
| Atomic life | 21, 110 | Photosphere | 35, 47 | |
| Azimuthal quantum number | 8, 204 | Quantum number | 8, 204 | |
| Boundary temperature | 27 | Quantum relation | 11 | |
| Displacement Rule | 13 | Residual intensity | 51 | |
| Effective level | 135 | Reversing layer | 47, 49 | |
| Effective temperature | 27 | Rydberg constant | 14, 155 | |
| Excitation potential | 15 | Saturation | 52, 135 | |
| Fractional concentration | 105 | Series notation | 55, 203 | |
| Inner quantum number | 204 | Spectroscopic valency | 10 | |
| Ionization potential | 15 | Subordinate lines | 12, 100 | |
| Ionization temperature | 30, 132 | Temperature class | 24, 112 | |
| Marginal appearance | 105, 135, 179 | Total quantum number | 8, 205 | |
| Optical depth | 27, 35 | Ultimate lines | 11, 111 | |
| Partial electron pressure | 10 | Valency | 10 | |
| Partition function | 107 | Wings | 50, 179 |
II. SERIES RELATIONS IN LINE SPECTRA
A SYNOPSIS of the normal series relations in line spectra has been published by Russell and Saunders (Ap. J., 61, 39, 1925). A transcription of the passages containing definitions of spectroscopic quantities that are mentioned in the present volume is given below:
“Every spectral line is now believed to be emitted (or absorbed) in connection with the transition of an atom (or molecule) between two definite (quantized) states, of different energy-content—the frequency of the radiation being exactly proportional to the change of energy. The wave-number of the line may therefore be expressed as the difference of two spectroscopic terms which measure, in suitable units, the energies of the initial and final states. Combinations between these terms occur according to definite laws, which enable us [Pg 204] to classify them into systems, each containing a number of series of terms, which are usually multiple—
“Any term may be expressed in the form
where
is the Rydberg constant and
an integer. For
homologous components of successive terms of the same series,
changes by unity, while the “residual”
is sometimes practically
constant (Rydberg’s formula), or, more often, is expressible in the
form
(Hicks’s formula), or
(Ritz’s formula).
In many cases this approximation fails for the smaller values of
;
and prediction becomes very uncertain, though a plot of the residuals
usually gives a smooth curve....
“The principles of selection, which determine what combinations among these numerous terms give rise to observable lines, are very simply expressed in terms of two sets of quantum numbers.
“The azimuthal quantum number () is i for all terms of the
s-series, 2 for those of the p-series, 3 for the d’s, 4 for the f’s, 5
for the g’s, 6 for the h’s, and so on.
“Combinations usually occur only between terms of adjacent series for
which the values of differ by a unit. A great many lines
are, however, known for which the change of
is 0, and a few for
which it is 2. In the simpler spectra, such lines are faint, except
when produced under the influence of a strong magnetic field; but in
the more complex spectra they are often numerous and strong.
“The inner quantum number () differs from one component of
a multiple term to another, and also in the various series and systems,
according to the following scheme.
| Series | Singlets | Doublets | Triplets | Quartets | Quintets | Sextets | Septets | |
|---|---|---|---|---|---|---|---|---|
| 1 | s | j = 0 | 1 | 1 | 2 | 2 | 3 | 3 |
| 2 | p | 1 | 1,2 | 0,1,2 | 1,2,3 | 1,2,3 | 2,3,4 | 2,3,4 |
| 3 | d | 2 | 2,3 | 1,2,3 | 1,2,3,4 | 0,1,2,3,4 | 1,2,3,4,5 | 1,2,3,4,5 |
| 4 | f | 3 | 3,4 | 2,3,4 | 2,3,4,5 | 1,2,3,4,5 | 1,2,3,4,5,6 | 0,1,2,3,4,5,6 |
| 5 | g | 4 | 4,5 | 3,4,5 | 3,4,5,6 | 2,3,4,5,6 | 2,3,4,5,6,7 | 1,2,3,4,5,6,7 |
“Combinations occur only between terms for which differs by 0 or
± 1. If, however,
in both cases, no radiation occurs. Lines
corresponding to a change of
are found in strong magnetic
fields, and a very few in their absence.
“The combination of two multiple terms gives rise, therefore, to a group of lines (which may number as many as eighteen). Such groups have been called multiplets by Catalan. Their discovery has afforded the key to the many-lined spectra....
“In such a group, those lines for which the changes in and
,
in passing from one term to the other, are of the same sign, are the
strongest, and those in which they are of opposite sign the weakest.
These intensity relations are of great assistance in picking out the
multiplets.
“Combinations between terms of different systems (consistent with the foregoing rules) often occur. Such lines are usually, though not always, faint....
“The serial number of the term (which is equivalent to the
total-quantum number) plays quite a subordinate rôle, being of
importance only when series formulae have to be calculated. An
extensive analysis of a spectrum is possible without it, though
determination of the limits of the series, and the ionization
potential, demands its introduction.”
[Pg 205]
THE line intensities quoted in Chapter VIII were derived from the spectra of the stars enumerated below in Table XXXII. Successive columns contain the Draper class, the name of the star, the Boss number, the visual apparent magnitude, and the reduced proper motion H. The stars within each class are arranged in order of right ascension.
| Class | Star | Boss | m | H | Class | Star | Boss | m | H | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cen | 3054 | 3.3 | 1.7 | Vel | 2723 | 4.1 | 5.1 | ||||
| Phe | 148 | 4.5 | -0.5 | Sgr | 4832 | 2.7 | 0.0 | ||||
| For | 474 | 4.7 | 0.1 | Gru | 5880 | 3.7 | 4.1 | ||||
| Eri | 6ll | 4.5 | 4.3 | Eri | 696 | 4.2 | 5.1 | ||||
| Dor | 1081 | 3.5 | 2.1 | Pic | 1446 | 3.9 | 3.7 | ||||
| Vel | 2356 | 2.0 | 1.9 | Mus | 3092 | 3.8 | 3.9 | ||||
| Car | 2493 | 1.8 | 3.2 | Pav | 5315 | 3.6 | 2.1 | ||||
| Cen | 3302 | 2.4 | 3.9 | PsA | 5916 | 1.3 | 4.1 | ||||
| TrA | 3879 | 3.1 | 2.2 | Hyi | 458 | 3.0 | 5.0 | ||||
| Sgr | 4645 | 2.0 | 2.7 | Car | 1622 | 0.9 | -4.6 [Pg 206] | ||||
| Car | 2503 | 2.2 | -0.7 | Crv | 3172 | 3.2 | 2.3 | ||||
| Boo | 3722 | 3.0 | 4.3 | Hyi | 3622 | 5.5 | 4.6 | ||||
| Cir | 3739 | 3.4 | 5.0 | Cen | 3623 | 2.3 | 6.7 | ||||
| TrA | 4030 | 3.0 | 6.2 | Lup | 3864 | 3.5 | 4.0 | ||||
| Sco | 4457 | 2.0 | -2.6 | Lib | 3962 | 5.3 | -1.2 | ||||
| Sco | 4361 | 3.4 | 5.7 | Apo | 4168 | 3.9 | 4.6 | ||||
| Sgr | 4874 | 3.0 | 1.0 | Sco | 4272 | 2.4 | 6.5 | ||||
| Vol | 1917 | 4.0 | 0.6 | Sgr | 4568 | 3.1 | 4.6 | ||||
| CMi | 2008 | 0.5 | 6.1 | Sgr | 4628 | 2.8 | 1.3 | ||||
| Pup | 2153 | 2.9 | 2.9 | Sgr | 4665 | 2.9 | 4.4 | ||||
| Vel | 2324 | 4.1 | 0.0 | Sgr | 4809 | 3.6 | 1.4 | ||||
| Oph | 4421 | 4.4 | 5.4 | Sgr | 4857 | 3.4 | 5.5 | ||||
| Sco | 4492 | 3.1 | -3.9 | Ind | 5281 | 3.2 | 2.5 | ||||
| Pav | 4778 | var. | 0.0 | Aqr | 5963 | 3.8 | 0.5 | ||||
| Tuc | 55 | 4.3 | 10.9 | Gru | 5965 | 4.1 | 4.9 | ||||
| For | 723 | 4.0 | 8.3 | Cru | 3218 | 3.6 | 5.1 | ||||
| Lep | 1420 | 3.8 | 9.7,7.1 | Mus | 3377 | 3.6 | 5.7 | ||||
| CMa | 1839 | 2.0 | -4.5 | TrA | 4250 | 1.9 | -0.6 | ||||
| Hyi | 74 | 2.9 | 9.7 | Ara | 4406 | 2.8 | 0.6 | ||||
| Aur | 1246 | 0.2 | 3.4 | Tuc | 5747 | 2.9 | 2.6 | ||||
| Lep | 1323 | 3.0 | 2.9 | Tau | 1077 | 1.1 | 2.6 | ||||
| Pup | 2065 | 3.5 | -2.3 | Pup | 1896 | 2.7 | -2.8 | ||||
| Leo | 2618 | 3.1 | 1.5 | Pup | 1972 | 3.3 | 4.7 | ||||
| Car | 2628 | var. | 1.1 | Car | 2739 | 3.4 | 1.7 | ||||
| Cap | 5507 | 3.9 | (1.1) | Apo | 3746 | 3.8 | 1.4 | ||||
| Ret | 994 | 3.4 | 2.6 | Ara | 4265 | 3.7 | 2.5 | ||||
| Vel | 2875 | 2.8 | 2.3 | Sco | 4292 | 3.8 | 5.9 | ||||
| Hya | 3042 | 3.7 | 5.3 | Ara | 4304 | 3.1 | 1.5 | ||||
| Crv | 3280 | 2.8 | 1.7 | And | 259 | 2.4 | -0.8 | ||||
| Hya | 3449 | 3.3 | 2.9 | Hyi | 899 | 3.2 | -1.3 | ||||
| CrA | 4871 | 4.2 | 2.0 | Ori | 1468 | 0.9 | -0.0 | ||||
| Pav | 5138 | 3.6 | 9.7 | Sco | 4193 | 1.2 | -2.5 | ||||
| Phe | 78 | 2.4 | 5.6 | Eri | 759 | 4.0 | 3.2 | ||||
| Cas | 135 | 2.5 | 1.4 | Cru | 3263 | 1.6 | 3.8 | ||||
| Phe | 245 | 3.4 | 1.6 | Lib | 3837 | 3.4 | 3.3 | ||||
| Phe | 336 | 4.0 | 5.4 | Her | 4373 | 3.5 | 0.9 | ||||
| Ret | 875 | 3.8 | 6.2 | Sgr | 4617 | 3.2 | 4.9 | ||||
| Lep | 1456 | 39 | 8.1 | Gru | 5854 | 2.2 | 2.8 | ||||
| Col | 1459 | 3.2 | 6.2 | ||||||||
[Pg 207]
IV. INTENSITY CHANGES OF LINES WITH UNKNOWN SERIES RELATIONS
THE following tabulation shows the intensity changes of lines of unknown series relations that occur in the hotter stars. The arrangement follows that of Table XIX. Notes on the maxima and blends are appended.
| Atom | Line | Note | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C++ | 4649 | 0.0 | 2.0 | 9.0 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | .. | 1 |
| N+ | 3996.9 | 0.0 | 0.0 | 0.0 | 0.0 | 5.0 | 6.0 | 7.0 | .. | 9.0 | .. | .. | 5.0 | 0.0 | 1 |
| N++ | 4515.0 | .. | 9.0 | 4.0 | 4.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2 |
| 4097.5 | .. | 15.0 | 8.0 | 5.0 | .. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3 | |
| O+ | 4943.4 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 4.0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1 |
| 4941.2 | |||||||||||||||
| 4705.3 | 0.0 | 0.0 | 0.0 | 2.0 | 4.0 | 4.0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2 | |
| 4699.2 | |||||||||||||||
| 4676.2 | 0.0 | 0.0 | 0.0 | 2.0 | 5.0 | .. | 7.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3 | |
| 4661.6 | 0.0 | 0.0 | 0.0 | 2.0 | 5.0 | .. | 7.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4 | |
| 4649.1 | 0.0 | 0.0 | 0.0 | 6.0 | 9.0 | 12.0 | 9.0 | .. | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5 | |
| 4641.8 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 10.0 | 7.0 | .. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6 | |
| 4596.2 | 0.0 | 0.0 | 0.0 | 1.0 | 5.0 | .. | 6.0 | .. | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7 | |
| 4591.0 | 0.0 | 0.0 | 0.0 | 1.0 | 5.0 | .. | 6.0 | .. | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 8 | |
| 4417.0 | 0.0 | 0.0 | 0.0 | 5.0 | 6.0 | 11.0 | 3.0 | .. | 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9 | |
| 4415.9 | 0.0 | 0.0 | 0.0 | 3.0 | .. | 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 10 | ||||
| 4366.9 | 0.0 | 4.0 | 4.0 | 4.0 | .. | 6.0 | 6.0 | .. | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 11 | |
| 4075.9 | 0.0 | 3.0 | 0.0 | 2.0 | 6.0 | 8.0 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 12 | |
| 4072.2 | 0.0 | 0.0 | 0.0 | 2.0 | 7.0 | 9.0 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 13 | |
| 4069.9 | 0.0 | 0.0 | 0.0 | 4.0 | 6.0 | 8.0 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 14 | |
| S+ | 4815 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | x | 0.0 | 0.0 | 0.0 | 1 |
| 4174.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 0.0 | 0.0 | 2 | |
| 4162.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 0.0 | 0.0 | 3 | |
| S++ | 4295 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4 |
| 4285.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.0 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 5 | |
| 4253.8 | 0.0 | 0.0 | 0.0 | 0.0 | 6.2 | 6.8 | 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6 |
NOTES TO TABLE XXXIII
| Atom | Note | Maximum | Remarks |
|---|---|---|---|
| C++ | 1 | Line blended, in stars cooler than |
|
| N+ | 1 | Unblended | |
| N++ | 2 | ||
| 3 | Blended with the Si+++ line at 4096, which is probably effective throughout the whole range | ||
| O+ | 1 | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | Blended with C++ line at 4649, which preponderates
in stars hotter than |
||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | Certainly another line is here involved, but it has not been identified | ||
| 12 | |||
| 13 | |||
| 14 | |||
| S+ | 1 2 3 | Lines recorded by Lockyer; not measured by the writer | |
| S++ | 4 | Line recorded by Lockyer. Intensity from H.A., 28; not measured by the writer | |
| 5 | |||
| 6 | Recorded by H. H. Plaskett in 10 Lacertae |
[Pg 208]
V. MATERIAL BEARING ON THE CLASSIFICATION OF STARS, QUOTED IN
CHAPTER XII
IN illustration of the problem of Class , observations of
sixty-two stars are collected in the following table. Successive
columns contain the H.D. number, the name of the star, the apparent
magnitude, the reduced proper motion
, and the spectral class.
Then follow columns which indicate the presence (
) or absence of
metallic lines, the quality of the lines (sharp lines being represented
by the letter
and hazy lines by the letter
), the presence
of wings to the hydrogen lines, and the strength of the Sr+ line at
4077 and the Si+ lines at 4128, 4131.
[Pg 209]
The stars in each class are arranged in order of increasing strength of metallic lines, and it will be seen that this feature is correlated with the strength of the silicon and strontium lines, but not with the line quality or the hydrogen wings, nor with the reduced proper motion.
| H. D. | Star | m | H | Class | Metalic Lines |
Line Quality |
H wings |
Sr+ | Si+ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 120198 | 84 | UMa | 5.53 | 6.4 | x | 9 | 10 | |||
| 108662 | 17 | Com | 5.38 | 2.7 | x | 7 | 8 | |||
| 170397 | Br | 2314 | 5.99 | 2.7 | x | h | 6 | 9 | ||
| 133029 | +47° | 2192 | 6.16 | - | x | h | 5 | 11 | ||
| 140160 | Ser | 5.26 | 3.5 | x | 10 | 5 | ||||
| 94334 | Uma | 4.34 | 3.6 | x | s | 2 | 3 | |||
| 58142 | 21 | Lyn | 4.45 | 2.9 | h | - | 4 | |||
| 192913 | +27° | 3668 | 6.69 | - | h | ? | 7 | |||
| 225132 | 2 | Cet | 4.62 | 1.2 | h | - | 4 | |||
| 41841 | 89 | Lep | 5.50 | 2.2 | - | - | ||||
| 222661 | Aqr | 4.62 | 4.8 | h | - | - | ||||
| 87887 | 15 | Sex | 4.6 | 1.9 | - | 5 | ||||
| 213323 | 38 | Peg | 5.51 | 3.3 | - | - | ||||
| 25642 | Per | 4.33 | 2.2 | - | 4 | |||||
| 114330 | Vir | 4.44 | 3.2 | s | - | 3 | ||||
| 109485 | 23 | Com | 4.78 | 4.1 | s | - | 3 | |||
| 103632 | Cra | 5.16 | 3.8 | x | - | - | ||||
| 110411 | Vir | 4.95 | 5.6 | x | - | - | ||||
| 133962 | k | Boo | 5.59 | 4.6 | x | - | - | |||
| 188260 | 13 | Vul | 4.50 | 2.5 | h | x | - | 4 | ||
| 124224 | 12 | 4.90 | 3.8 | - | 11 | |||||
| 183056 | 4 | Cyg | 5.2 | -0.4 | - | 9 | ||||
| 183986 | +35° | 3658 | 6.04 | - | x | - | 5 | |||
| 196502 | 73 | Dra | 5.18 | 1.2 | x | s | 12 | 10 | ||
| 148367 | Oph | 4.68 | 4.3 | x | s | x | 9 | 8 | ||
| 118022 | 78 | Vir | 4.93 | 3.5 | x | 10 | 9 | |||
| 182564 | Dra | 4.63 | 2.9 | x | 7 | 7 | ||||
| 125337 | Vir | 4.60 | -1.9 | x | h | 7 | 6 | |||
| 214734 | 30 | Cep | 5.21 | 1.6 | x | 3? | 5 | |||
| 7804 | 89 | Psc | 5.28 | 4.2 | x | x | 5 | 7 | ||
| 220825 | Psc | 4.94 | - | x | 6 | 7 | ||||
| 72968 | 3 | Hya | 5.61 | 2.8 | x | 6 | 7 | |||
| 56405 | Paris | 8971 | 5.39 | 4.7 | x | s | s | 3? | 6 | |
| 20677 | 32 | Per | 4.98 | 3.8 | x | x | - | 5 [Pg 210] | ||
| 48250 | 12 | Lyn | 4.89 | 1.8 | x | x | - | 5 | ||
| 107612 | - | Com | 6.56 | - | x | 9 | - | |||
| 18519,20 | Ari | 4.6 | 1.1 | s | 3 | 3 | ||||
| 107966 | 13 | Com | 5.10 | 2.7 | - | - | ||||
| 108382 | 16 | Com | 5.04 | 0.6 | - | - | ||||
| 108945 | 21 | Com | 5.39 | 1.9 | x | 11 | 9 | |||
| 108642 | +26° | 2138 | 6.48 | - | x | 8 | 6 | |||
| 89904 | 27 | Lmi | 6.1 | 3.0 | x | h | x | 6 | 9 | |
| 108651 | +26° | 2353 | 6.69 | - | x | h | 7 | 6 | ||
| 170296 | Scu | 4.73 | -0.5 | x | h | x | - | 7 | ||
| 115331 | 196 | Cen | 6.0 | 3.4 | h | 9 | - | |||
| 108486 | +26° | 2352 | 6.57 | - | 7 | - | ||||
| 104321 | Vir | 4.57 | 2.2 | 5 | - | |||||
| 222345 | Aqr | 5.16 | 4.6 | x | - | 9 | ||||
| 14690 | 70 | Cet | 5.62 | 4.3 | x | 7 | ? | |||
| 189849 | 15 | Vul | 4.74 | 3.3 | x | s | x | 9 | 6 | |
| 28546 | 81 | Tau | 5.49 | 5.7 | x | 9 | 9 | |||
| 40536 | 2 | Mon | 5.10 | 4.0 | x | h? | 7 | 7 | ||
| 15089 | Cas | 4.59 | 0.5 | x | 12 | 9 | ||||
| 91312 | Gr | 1658 | 4.85 | 5.6 | x | s | x | 5 | 6 | |
| 159560 | Dra | 4.95 | 6.0 | 8 | - | |||||
| 90277 | 30 | Lmi | 4.85 | 5.0 | x | 9 | 9 | |||
| 57749 | 86 | 5.83 | 2.3 | x | 9 | 6 | ||||
| 92787 | 135 | 5.28 | 7.6 | x | s | 9 | 6 | |||
| 112429 | 8 | Dra | 5.27 | 3.0 | x | 7 | 7 | |||
| 28485 | 80 | Tau | 5.70 | 5.8 | h | 6 | 5 | |||
| 28677 | 85 | Tau | 6.04 | - | - | 7 | - | |||
[Pg 211]
[Pg 214]